AtCoder Beginner Contest 371（ABCDE）

A

个人直接硬解，讨论情况也并不复杂

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
void solve() {
    char a, b, c;
    cin >> a >> b >> c;
    if (a == '<') {
        if (c == '<') {
            cout << "B" << endl;
            return;
        } else {
            if (b == '<') {
                cout << "C" << endl;
                return;
            } else {
                cout << "A" << endl;
                return;
            }
        }
    } else {
        if (c == '>') {
            cout << "B" << endl;
            return;
        } else {
            if (b == '<') {
                cout << "A" << endl;
                return;
            } else {
                cout << "C" << endl;
                return;
            }
        }
    }
}
signed main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
//    int t;
//    cin >> t;
//    while (t--)
    solve();
    return 0;
}

B

只要一旦找到每个家庭的太郎，标记一下就行了

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
bool vt[N];
void solve() {
    int n, m;
    cin >> n >> m;
    while (m--) {
        int a;
        char c;
        cin >> a >> c;
        if (!vt[a]) {
            if (c == 'M') {
                cout << "Yes" << endl;
                vt[a] = 1;
            } else {
                cout << "No" << endl;
            }
        } else cout << "No" << endl;
    }
}
signed main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
//    int t;
//    cin >> t;
//    while (t--)
    solve();
    return 0;
}

C

同构见的不是很多，但该题数据很小，点最多才8个，第一眼的思路是对第二个图的点进行全排列，然后再与图一比较，计算删边和加边的总价值，然后对每个全排列的总价值取最小就是最终答案，代码细节比较多。

如果数据范围较大，确实有必要思考一下怎么做。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=10;
int w[N][N];//加边或删边的权值
int a[N];//全排列
bool p1[N][N],p2[N][N];//分别为图一图二的边
bool vis[N][N];//用于标记，避免重复加边或删边
void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        p1[u][v] = 1, p1[v][u] = 1;//反向也记录
    }
    int M;
    cin >> M;
    for (int i = 1; i <= M; i++) {
        int u, v;
        cin >> u >> v;
        p2[u][v] = 1, p2[v][u] = 1;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = i + 1; j <= n; j++) {
            cin >> w[i][j];
            w[j][i] = w[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        a[i] = i;
    }
    int ans1 = 1e16;
    do {
        memset(vis, 0, sizeof vis);
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if ((!vis[a[i]][a[j]] && !vis[a[j]][a[i]]) &&
                    ((p1[i][j] && !p2[a[i]][a[j]]) || (!p1[i][j] && p2[a[i]][a[j]]))) {
                    ans += w[a[i]][a[j]];
                    vis[a[i]][a[j]] = vis[a[j]][a[i]] = 1;//标记该边已经被处理
                }
            }
        }
        ans1 = min(ans, ans1);
    } while (next_permutation(a + 1, a + n + 1));//全排列函数
    cout << ans1 << endl;
}
signed main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
//    int t;
//    cin >> t;
//    while (t--)
    solve();
    return 0;
}

D

D题相当模板，查询区间的和，直接上线段树，但该题是以坐标的形式，所有首先是要将坐标的范围转变为下标的区间，以便线段树区间查询。对于左端点，二分去找第一个≥该坐标的下标就是区间左端点；

对于右端点二分去找第一个大于该坐标的下标再减一就是区间右端点；

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
#define lc p<<1
#define rc (p<<1)|1
const int N=2e5+10;
int x[N],b[N];
struct Tree {
    int l, r, sum;
}tr[N*4];

void pushup(int p) { //上传
    tr[p].sum = tr[lc].sum + tr[rc].sum;
}

void build(int p,int l,int r) { //建树
    tr[p] = {l, r, b[l]};
    if (l == r) return;
    int m = l + r >> 1;
    build(lc, l, m);
    build(rc, m + 1, r);
    pushup(p);
}

int query(int p,int x,int y) { //区间查询
    if (x <= tr[p].l && y >= tr[p].r) { //覆盖则返回
        return tr[p].sum;
    }
    int m = tr[p].l + tr[p].r >> 1; //不覆盖裂开
//    pushdown(p);
    int sum = 0;
    if (x <= m) sum += query(lc, x, y);
    if (y > m) sum += query(rc, x, y);
    return sum;
}

void solve() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> x[i];
    }
    for (int i = 1; i <= n; i++) cin >> b[i];
    build(1, 1, n);
    int q;
    cin >> q;
    while (q--) {
        int l, r;
        cin >> l >> r;
        int l1 = lower_bound(x + 1, x + n + 1, l) - x;
        int r1 = upper_bound(x + 1, x + n + 1, r) - x - 1;
        if (r1 < l1) cout << 0 << endl;
        else cout << query(1, l1, r1) << endl;
    }
}
signed main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
//    int t;
//    cin >> t;
//    while (t--)
        solve();
    return 0;
}

E

对于每一个值a[i]，包含它的区间的个数是(n - j + 1) * j ，也就是它的贡献。但是，有相同的数，所以造成的贡献就不一样，要取相同的俩个值中间的部分作为贡献

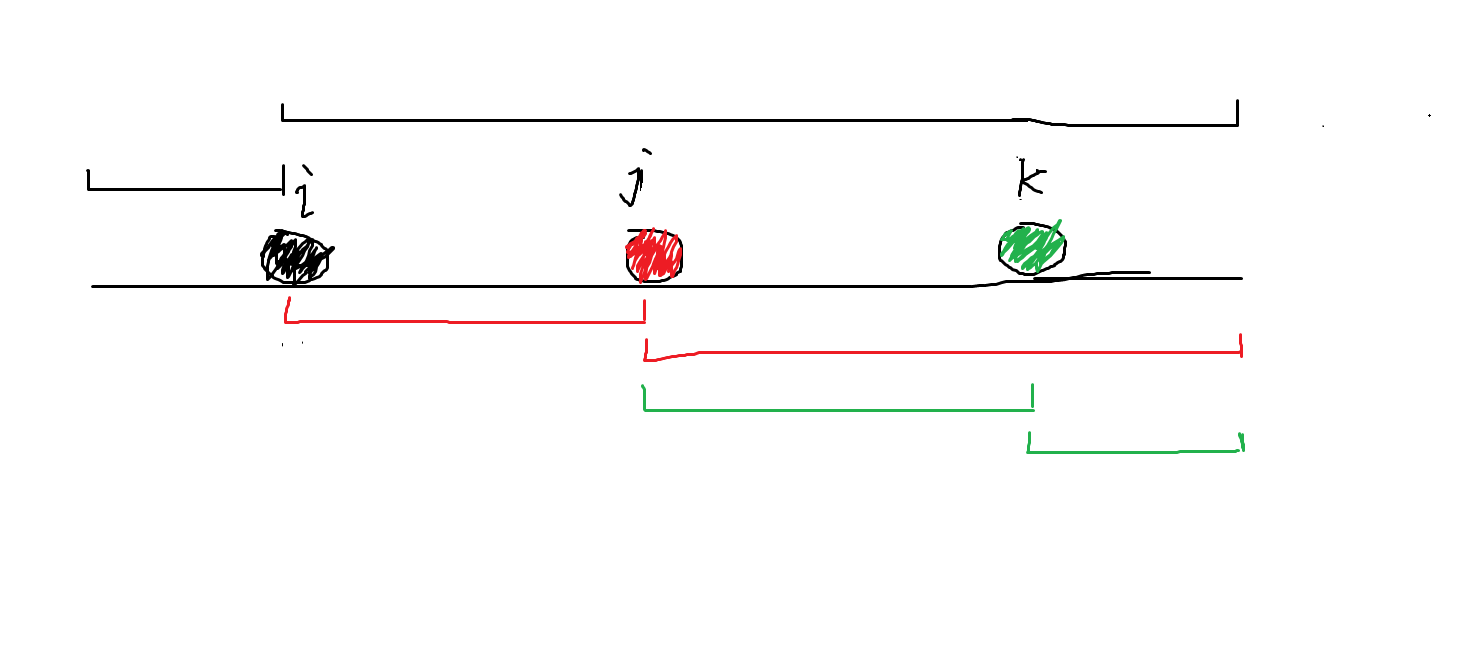
像这样每个元素对应的贡献是这样的俩段区间长度的乘积，图中的贡献就是 i*(n - i + 1) + (j - i) * (n - j + 1) + (k - j) * (n - k + 1)

所以将每种值的元素的所有下标放到一个数组中，然后加上每种值的元素的贡献就能得出答案

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=2e5+10;
int a[N];
vector<int> p[N];//p[i]存放值为i所有的元素所在的下标
void solve() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        p[a[i]].push_back(i);
    }
    int ans = 0;
    for (int i = 1; i <= n; i++) {//每种不同值的元素
        int cnt = 0;
        for (auto j: p[i]) {//所在下标
            ans += (n - j + 1) * (j - cnt);
            cnt = j;
        }
    }
    cout << ans << endl;
}
signed main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
//    int t;
//    cin >> t;
//    while (t--)
    solve();
    return 0;
}

总结：

C>D, E题很巧妙，用不上数据结构