深入理解图优化与g2o：g2o篇

内容提要

　　讲完了优化的基本知识，我们来看一下g2o的结构。本篇将讨论g2o的代码结构，并带着大家一起写一个简单的双视图bundle adjustment：从两张图像中估计相机运动和特征点位置。你可以把它看成一个基于稀疏特征点的单目VO。

g2o的结构

　　g2o全称是什么？来跟我大声说一遍：General Graph Optimization！你可以叫它g土o，g二o，g方o，总之我也不知道该怎么叫它……

　　所谓的通用图优化。

　　为何叫通用呢？g2o的核里带有各种各样的求解器，而它的顶点、边的类型则多种多样。通过自定义顶点和边，事实上，只要一个优化问题能够表达成图，那么就可以用g2o去求解它。常见的，比如bundle adjustment，ICP，数据拟合，都可以用g2o来做。甚至我还在想神经网络能不能写成图优化的形式呢……

　　从代码层面来说，g2o是一个c++编写的项目，用cmake构建。它的github地址在：https://github.com/RainerKuemmerle/g2o

　　它是一个重度模板类的c++项目，其中矩阵数据结构多来自Eigen。首先我们来扫一眼它的目录下面都有什么吧：

　　如你所见，g2o项目中含有若干文件夹。刨开那些gitignore之类的零碎文件，主要有以下几个：

EXTERNAL　　三方库，有ceres, csparse, freeglut，可以选择性地编译；
cmake_modules　　给cmake用来寻找库的文件。我们用g2o时也会用它里头的东西，例如FindG2O.cmake
doc　　　　　文档。包括g2o自带的说明书（难度挺大的一个说明文档）。
g2o　　　　　　最重要的源代码都在这里！
script　　　　在android等其他系统编译用的脚本，由于我们在ubuntu下就没必要多讲了。

　　综上所述，最重要的就是g2o的源代码文件啦！所以我们要进一步展开看一看！

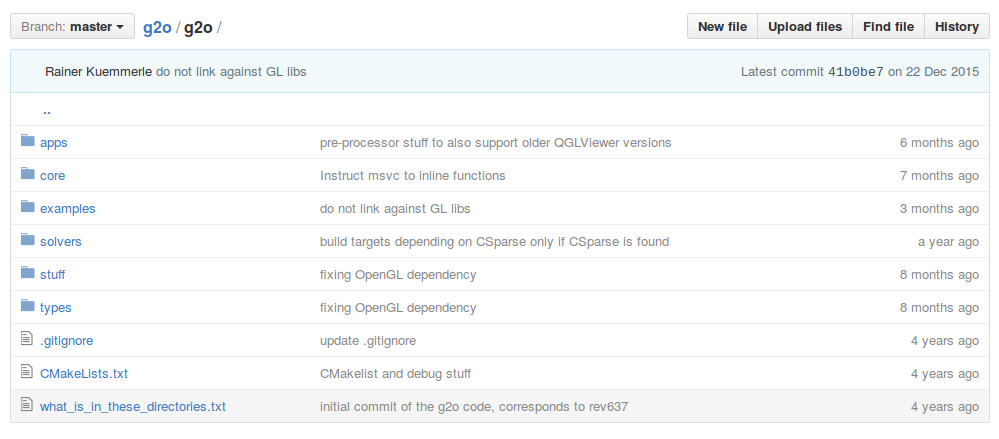
　　我们同样地介绍一下各文件夹的内容：

apps　　　　一些应用程序。好用的g2o_viewer就在这里。其他还有一些不常用的命令行工具等。
core　　　　核心组件，很重要！基本的顶点、边、图结构的定义，算法的定义，求解器接口的定义在这里。
examples　　一些例程，可以参照着这里的东西来写。不过注释不太多。
solvers　　　　求解器的实现。主要来自choldmod, csparse。在使用g2o时要先选择其中一种。
stuff　　　　对用户来讲可有可无的一些工具函数。
types　　　　各种顶点和边，很重要！我们用户在构建图优化问题时，先要想好自己的顶点和边是否已经提供了定义。如果没有，要自己实现。如果有，就用g2o提供的即可。

　　就经验而言，solvers给人的感觉是大同小异，而 types 的选取，则是 g2o 用户主要关心的内容。然后 core 下面的内容，我们要争取弄的比较熟悉，才能确保使用中出现错误可以正确地应对。

　　那么，g2o最基本的类结构是怎么样的呢？我们如何来表达一个Graph，选择求解器呢？我们祭出一张图：

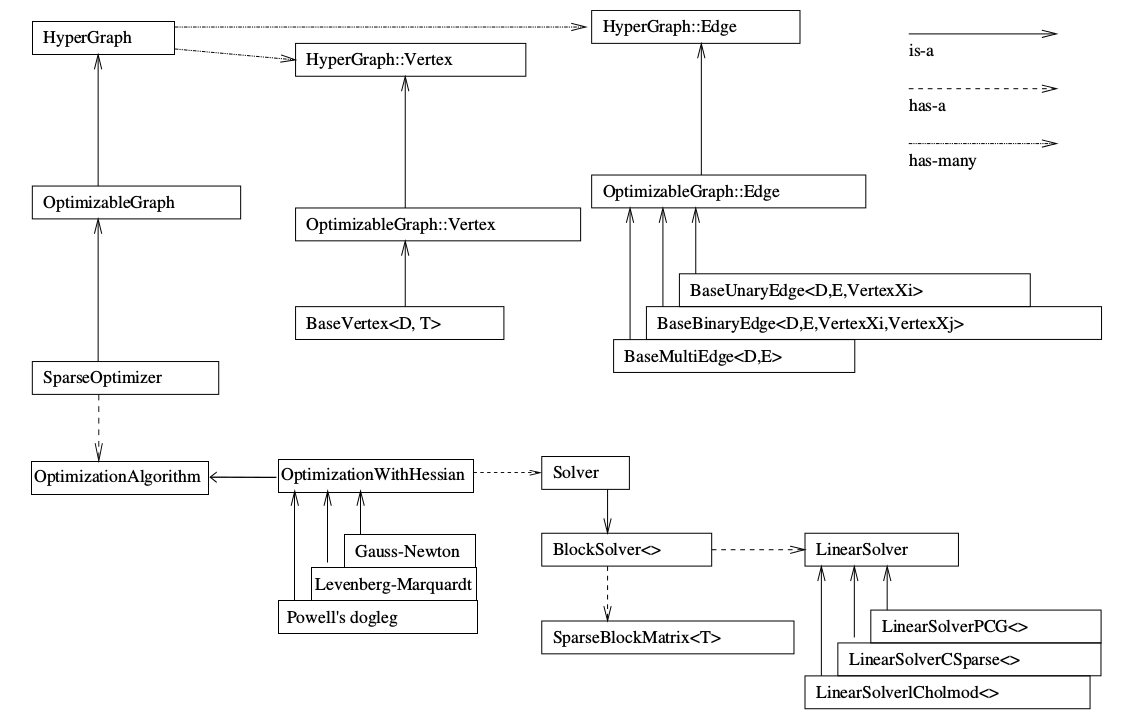
　　这个图第一次看，可能觉得有些混乱。但是随着g2o越用越多，你会发现越来越喜欢这个图……现在请读者跟着我的顺序来看这个图。

　　先看上半部分。SparseOptimizer 是我们最终要维护的东东。它是一个Optimizable Graph，从而也是一个Hyper Graph。一个 SparseOptimizer 含有很多个顶点（都继承自 Base Vertex）和很多个边（继承自 BaseUnaryEdge, BaseBinaryEdge或BaseMultiEdge）。这些 Base Vertex 和 Base Edge 都是抽象的基类，而实际用的顶点和边，都是它们的派生类。我们用 SparseOptimizer.addVertex 和 SparseOptimizer.addEdge 向一个图中添加顶点和边，最后调用 SparseOptimizer.optimize 完成优化。

　　在优化之前，需要指定我们用的求解器和迭代算法。从图中下半部分可以看到，一个 SparseOptimizer 拥有一个 Optimization Algorithm，继承自Gauss-Newton, Levernberg-Marquardt, Powell's dogleg 三者之一（我们常用的是GN或LM）。同时，这个 Optimization Algorithm 拥有一个Solver，它含有两个部分。一个是 SparseBlockMatrix ，用于计算稀疏的雅可比和海塞；一个是用于计算迭代过程中最关键的一步 $$H \Delta x = -b $$ 这就需要一个线性方程的求解器。而这个求解器，可以从 PCG, CSparse, Choldmod 三者选一。

　　综上所述，在g2o中选择优化方法一共需要三个步骤：

选择一个线性方程求解器，从 PCG, CSparse, Choldmod中选，实际则来自 g2o/solvers 文件夹中定义的东东。
选择一个 BlockSolver 。
选择一个迭代策略，从GN, LM, Doglog中选。

　　这样一来，读者是否对g2o就更清楚的认识了呢？

　　小萝卜：师兄你慢点，我已经晕了……

双视图bundle adjustment：

　　既然小萝卜同学已经晕了，想必我们也成功地把读者朋友都绕进去了。既绕之则绕之，下面我们来通过一个实例，更深入地理解 g2o 的用法。这个实例是什么呢？我们来写一个双视图的bundle adjustment吧！

　　代码的git地址：https://github.com/gaoxiang12/g2o_ba_example

　　首先，师兄还是拿出那两张万年不变的老图：

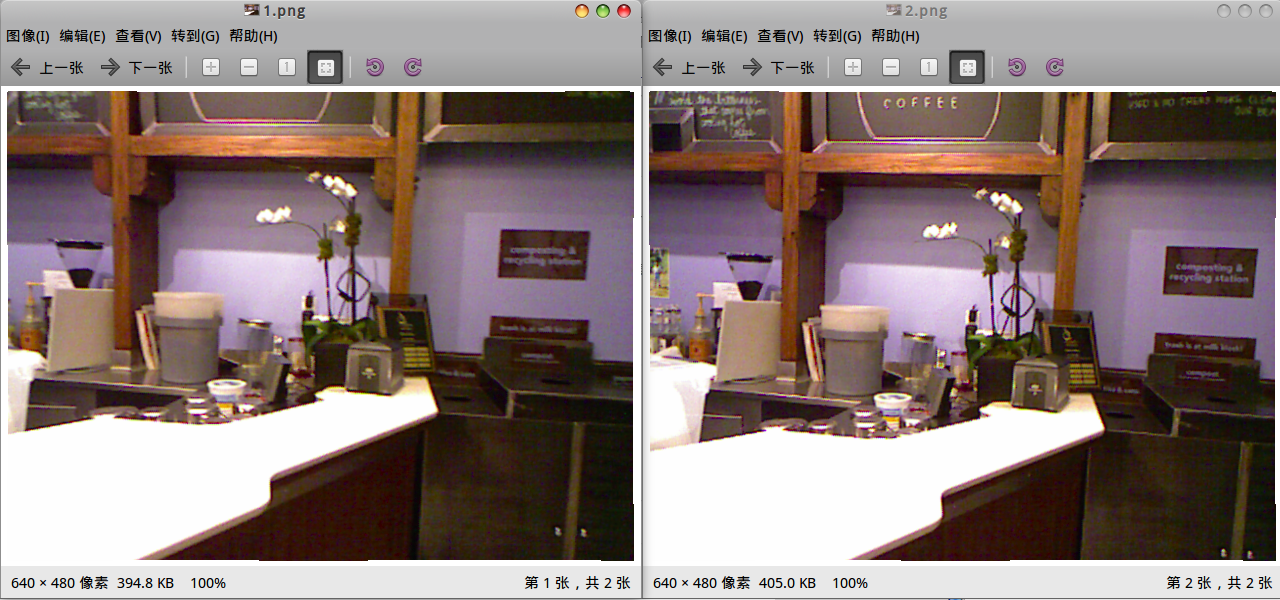
　　我们的目标是估计这两个图之间的运动。虽然我们在《一起做》里讲过这件事怎么做了，但那是在RGBD的条件下。现在，我们没有深度图，只有这两张图像和相机内参，请问如何估计相机的运动？

　　呃，这个问题好像还挺复杂的。我们需要用一点数学来描述它。所以请大家耐心看我推一会儿公式。

　　求解这个问题，当下有两种思路。其一是通过特征点来求，其二是直接通过像素来求。第一种也叫做 sparse 方式，第二种叫做相对的 dense 方式。由于主流仍在用特征点，所以我们例程也用特征点。

　　特征点方法的观点是：一个图像可以用几百个具有代表性的，比较稳定的点来表示。一旦我们有了这些点，就可以忽略图中的其余部分，而只关注这些点。（dense 思路则反对这一观点，认为它丢弃了图像大部分信息，毕竟一个640x480的图有30万个点，而特征点只有几百个）。

　　采用特征点的思路，那么问题变为：给定$N$个两张图中一一对应的点，记作：$${z_1} = \left\{ {z_1^1,z_1^2, \ldots ,z_1^N} \right\},{z_2} = \left\{ {z_2^1,z_2^2, \ldots ,z_2^N} \right\} $$ 以及相机内参矩阵 $C$，求解两个图中的相机运动$R,t$。

　　注：字符$z$的上标不是几次方的意思，而是第几个点。采用上标的原因是为了避免双下标带来的麻烦。同时，每个点的具体值$z$，是指该点对应的像素坐标：$z_i^j = [u,v]_i^j$，它们是二维的。

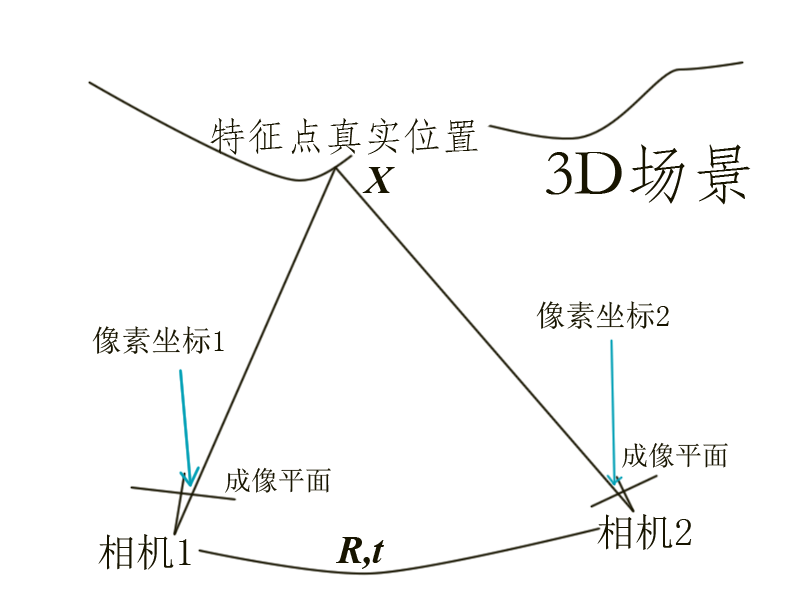
　小萝卜：师兄啊，这图一股浓浓的山寨味啊。

　　不管它，总之，假设相机1的位姿为单位矩阵，对于任意一个特征点，它在三维空间的真实坐标位于 $X^j$，而在两个相机坐标系上看来是 $z_1^j, z_2^j$。根据投影关系，我们有：

\[ \begin{equation} {\lambda _1}\left[ \begin{array}{l}
z_1^j\\
1
\end{array} \right] = C{X^j},\quad {\lambda _2}\left[ \begin{array}{l}
z_2^j\\
1
\end{array} \right] = C\left( {R{X^j} + t} \right) \end{equation}\]

　　这里的 $\lambda_1, \lambda_2$ 表示两个像素的深度值，说白了也就是相机1坐标下$X^j$的$z$坐标。虽然我们不知道这个实际的$X^j$是什么，但它和$z$之间的关系，是可以列写出来的。

　　这个问题的传统求解方式，是把两个方程中的$X^j$消去，得到只关于$z, R, t$的关系式，然后进行优化。这条道路通向对极几何和基础矩阵（Essential Matrix），理论上，我们需要大于八个的匹配点就能计算出$R,t$。但这里我们并不这样做，因为我们是在介绍图优化嘛。

　　在图优化中，我们构建一个优化问题，并表示成图去求解。这里的优化问题是什么呢？这可以这样写：

\[ \begin{equation} \mathop {\min }\limits_{{X^j},R,t} {\left\| {\frac{1}{{{\lambda _1}}}C{X^j} - {{\left[ {z_1^j,1} \right]}^T}} \right\|^2} + {\left\| {\frac{1}{{{\lambda _2}}}C\left( {R{X^j} + t} \right) - {{\left[ {z_2^j,1} \right]}^T}} \right\|^2} \end{equation} \]

　　由于各种噪声的存在，投影关系不能完美满足，所以我们转而优化它们误差的二范数。那么对每一个特征点，我们都能写出这样一个二范数的误差项。对它们进行求和，就得到了整个优化问题：

\[ \begin{equation} \mathop {\min }\limits_{X,R,t} \sum\limits_{j = 1}^N {{{\left\| {\frac{1}{{{\lambda _1}}}C{X^j} - {{\left[ {z_1^j,1} \right]}^T}} \right\|}^2} + {{\left\| {\frac{1}{{{\lambda _2}}}C\left( {R{X^j} + t} \right) - {{\left[ {z_2^j,1} \right]}^T}} \right\|}^2}} \end{equation} \]

　　它叫做最小化重投影误差问题（Minimization of Reprojection error）。当然，它很遗憾地，是个非线性，非凸的优化问题，这意味着我们不一定能求解它，也不一定能找到全局最优的解。在实际操作中，我们实际上是在调整每个$X^j$，使得它们更符合每一次观测$z^j$，也就是使每个误差项都尽量的小。由于这个原因，它也叫做捆集调整（Bundle Adjustment）。

　　BA很容易表述成图优化的形式。在这个双视图BA中，一种有两种结点：

相机位姿结点：表达两个相机所在的位置，是一个$SE(3)$里的元素。
特征点的空间位置结点：是一个XYZ坐标。

　　相应的，边主要表示空间点到像素坐标的投影关系。也就是

\[\lambda \left[ \begin{array}{l}
{z^j}\\
1
\end{array} \right] = C\left( {R{X^j} + t} \right)\] 这件事情喽。

实现

　　下面我们来用g2o实现一下BA。选取的结点和边如下：

结点1：相机位姿结点：g2o::VertexSE3Expmap，来自<g2o/types/sba/types_six_dof_expmap.h>；
结点2：特征点空间坐标结点：g2o::VertexSBAPointXYZ，来自<g2o/types/sba/types_sba.h>；
边：重投影误差：g2o::EdgeProjectXYZ2UV，来自<g2o/types/sba/types_six_dof_expmap.h>；

　　为了给读者更深刻的印象，我们显示一下边的源码（也请读者最好亲自打开g2o下这几个文件看一下顶点和边的定义）：

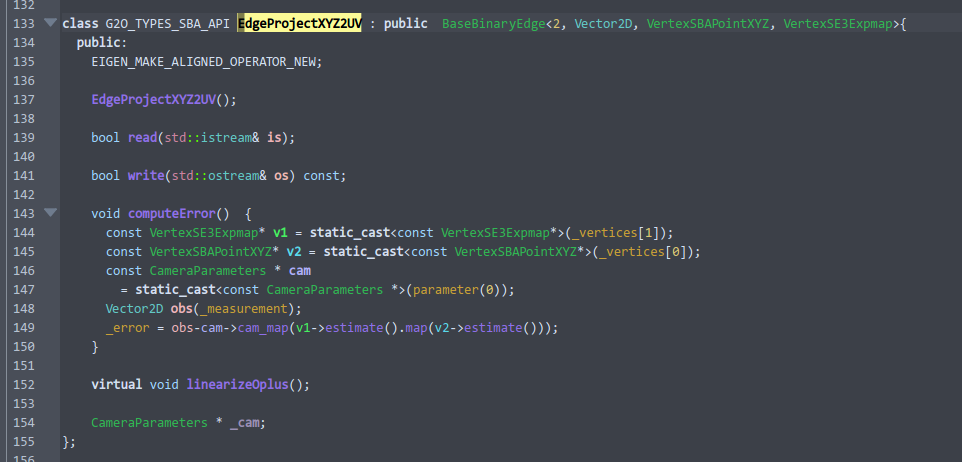
　　这个是 EdgeProjectXYZ2UV 边的定义。它是一个Binary Edge，后面的模板参数表示，它的数据是2维的，来自Eigen::Vector2D，它连接的两个顶点必须是 VertexSBAPointXYZ， VertexSE3Expmap。我们还能看到它的 computeError 定义，和前面给出的公式是一致的。注意到计算Error时，它调用了 g2o::CameraParameters 作为参数，所以我们在设置这条边时也需要给定一个相机参数。

　　铺垫了那么多之后，给出我们的源码：

 /**

  * BA Example

  * Author: Xiang Gao

  * Date: 2016.3

  * Email: gaoxiang12@mails.tsinghua.edu.cn

  *

  * 在这个程序中，我们读取两张图像，进行特征匹配。然后根据匹配得到的特征，计算相机运动以及特征点的位置。这是一个典型的Bundle Adjustment，我们用g2o进行优化。

  */

 // for std

 #include <iostream>

 // for opencv

 #include <opencv2/core/core.hpp>

 #include <opencv2/highgui/highgui.hpp>

 #include <opencv2/features2d/features2d.hpp>

 #include <boost/concept_check.hpp>

 // for g2o

 #include <g2o/core/sparse_optimizer.h>

 #include <g2o/core/block_solver.h>

 #include <g2o/core/robust_kernel.h>

 #include <g2o/core/robust_kernel_impl.h>

 #include <g2o/core/optimization_algorithm_levenberg.h>

 #include <g2o/solvers/cholmod/linear_solver_cholmod.h>

 #include <g2o/types/slam3d/se3quat.h>

 #include <g2o/types/sba/types_six_dof_expmap.h>

 using namespace std;

 // 寻找两个图像中的对应点，像素坐标系

 // 输入：img1, img2 两张图像

 // 输出：points1, points2, 两组对应的2D点

 int     findCorrespondingPoints( const cv::Mat& img1, const cv::Mat& img2, vector<cv::Point2f>& points1, vector<cv::Point2f>& points2 );

 // 相机内参

 double cx = 325.5;

 double cy = 253.5;

 double fx = 518.0;

 double fy = 519.0;

 int main( int argc, char** argv )

 {

     // 调用格式：命令 [第一个图] [第二个图]

     if (argc != )

     {

         cout<<"Usage: ba_example img1, img2"<<endl;

         exit();

     }

     // 读取图像

     cv::Mat img1 = cv::imread( argv[] );

     cv::Mat img2 = cv::imread( argv[] ); 

     // 找到对应点

     vector<cv::Point2f> pts1, pts2;

     if ( findCorrespondingPoints( img1, img2, pts1, pts2 ) == false )

     {

         cout<<"匹配点不够！"<<endl;

         return ;

     }

     cout<<"找到了"<<pts1.size()<<"组对应特征点。"<<endl;

     // 构造g2o中的图

     // 先构造求解器

     g2o::SparseOptimizer    optimizer;

     // 使用Cholmod中的线性方程求解器

     g2o::BlockSolver_6_3::LinearSolverType* linearSolver = new  g2o::LinearSolverCholmod<g2o::BlockSolver_6_3::PoseMatrixType> ();

     // 6*3 的参数

     g2o::BlockSolver_6_3* block_solver = new g2o::BlockSolver_6_3( linearSolver );

     // L-M 下降

     g2o::OptimizationAlgorithmLevenberg* algorithm = new g2o::OptimizationAlgorithmLevenberg( block_solver );

     optimizer.setAlgorithm( algorithm );

     optimizer.setVerbose( false );

     // 添加节点

     // 两个位姿节点

     for ( int i=; i<; i++ )

     {

         g2o::VertexSE3Expmap* v = new g2o::VertexSE3Expmap();

         v->setId(i);

         if ( i == )

             v->setFixed( true ); // 第一个点固定为零

         // 预设值为单位Pose，因为我们不知道任何信息

         v->setEstimate( g2o::SE3Quat() );

         optimizer.addVertex( v );

     }

     // 很多个特征点的节点

     // 以第一帧为准

     for ( size_t i=; i<pts1.size(); i++ )

     {

         g2o::VertexSBAPointXYZ* v = new g2o::VertexSBAPointXYZ();

         v->setId(  + i );

         // 由于深度不知道，只能把深度设置为1了

         double z = ;

         double x = ( pts1[i].x - cx ) * z / fx;

         double y = ( pts1[i].y - cy ) * z / fy;

         v->setMarginalized(true);

         v->setEstimate( Eigen::Vector3d(x,y,z) );

         optimizer.addVertex( v );

     }

     // 准备相机参数

     g2o::CameraParameters* camera = new g2o::CameraParameters( fx, Eigen::Vector2d(cx, cy),  );

     camera->setId();

     optimizer.addParameter( camera );

     // 准备边

     // 第一帧

     vector<g2o::EdgeProjectXYZ2UV*> edges;

     for ( size_t i=; i<pts1.size(); i++ )

     {

         g2o::EdgeProjectXYZ2UV*  edge = new g2o::EdgeProjectXYZ2UV();

         edge->setVertex( , dynamic_cast<g2o::VertexSBAPointXYZ*>   (optimizer.vertex(i+)) );

         edge->setVertex( , dynamic_cast<g2o::VertexSE3Expmap*>     (optimizer.vertex()) );

         edge->setMeasurement( Eigen::Vector2d(pts1[i].x, pts1[i].y ) );

         edge->setInformation( Eigen::Matrix2d::Identity() );

         edge->setParameterId(, );

         // 核函数

         edge->setRobustKernel( new g2o::RobustKernelHuber() );

         optimizer.addEdge( edge );

         edges.push_back(edge);

     }

     // 第二帧

     for ( size_t i=; i<pts2.size(); i++ )

     {

         g2o::EdgeProjectXYZ2UV*  edge = new g2o::EdgeProjectXYZ2UV();

         edge->setVertex( , dynamic_cast<g2o::VertexSBAPointXYZ*>   (optimizer.vertex(i+)) );

         edge->setVertex( , dynamic_cast<g2o::VertexSE3Expmap*>     (optimizer.vertex()) );

         edge->setMeasurement( Eigen::Vector2d(pts2[i].x, pts2[i].y ) );

         edge->setInformation( Eigen::Matrix2d::Identity() );

         edge->setParameterId(,);

         // 核函数

         edge->setRobustKernel( new g2o::RobustKernelHuber() );

         optimizer.addEdge( edge );

         edges.push_back(edge);

     }

     cout<<"开始优化"<<endl;

     optimizer.setVerbose(true);

     optimizer.initializeOptimization();

     optimizer.optimize();

     cout<<"优化完毕"<<endl;

     //我们比较关心两帧之间的变换矩阵

     g2o::VertexSE3Expmap* v = dynamic_cast<g2o::VertexSE3Expmap*>( optimizer.vertex() );

     Eigen::Isometry3d pose = v->estimate();

     cout<<"Pose="<<endl<<pose.matrix()<<endl;

     // 以及所有特征点的位置

     for ( size_t i=; i<pts1.size(); i++ )

     {

         g2o::VertexSBAPointXYZ* v = dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(i+));

         cout<<"vertex id "<<i+<<", pos = ";

         Eigen::Vector3d pos = v->estimate();

         cout<<pos()<<","<<pos()<<","<<pos()<<endl;

     }

     // 估计inlier的个数

     int inliers = ;

     for ( auto e:edges )

     {

         e->computeError();

         // chi2 就是 error*\Omega*error, 如果这个数很大，说明此边的值与其他边很不相符

         if ( e->chi2() >  )

         {

             cout<<"error = "<<e->chi2()<<endl;

         }

         else

         {

             inliers++;

         }

     }

     cout<<"inliers in total points: "<<inliers<<"/"<<pts1.size()+pts2.size()<<endl;

     optimizer.save("ba.g2o");

     return ;

 }

 int     findCorrespondingPoints( const cv::Mat& img1, const cv::Mat& img2, vector<cv::Point2f>& points1, vector<cv::Point2f>& points2 )

 {

     cv::ORB orb;

     vector<cv::KeyPoint> kp1, kp2;

     cv::Mat desp1, desp2;

     orb( img1, cv::Mat(), kp1, desp1 );

     orb( img2, cv::Mat(), kp2, desp2 );

     cout<<"分别找到了"<<kp1.size()<<"和"<<kp2.size()<<"个特征点"<<endl;

     cv::Ptr<cv::DescriptorMatcher>  matcher = cv::DescriptorMatcher::create( "BruteForce-Hamming");

     double knn_match_ratio=0.8;

     vector< vector<cv::DMatch> > matches_knn;

     matcher->knnMatch( desp1, desp2, matches_knn,  );

     vector< cv::DMatch > matches;

     for ( size_t i=; i<matches_knn.size(); i++ )

     {

         if (matches_knn[i][].distance < knn_match_ratio * matches_knn[i][].distance )

             matches.push_back( matches_knn[i][] );

     }

     if (matches.size() <= ) //匹配点太少

         return false;

     for ( auto m:matches )

     {

         points1.push_back( kp1[m.queryIdx].pt );

         points2.push_back( kp2[m.trainIdx].pt );

     }

     return true;

 }

　　在这个程序中，我们从命令行参数读取两个图像所在的位置，然后构建一个图估计图像间运动和特征点的空间位置。

　　整个工程的编译方式使用cmake，请参考 github 工程进行编译，这里就不详细说明了。（因为肯定又要提一堆Cmake方面的事情。）

　　编译完成后，可以运行此程序，结果如下：

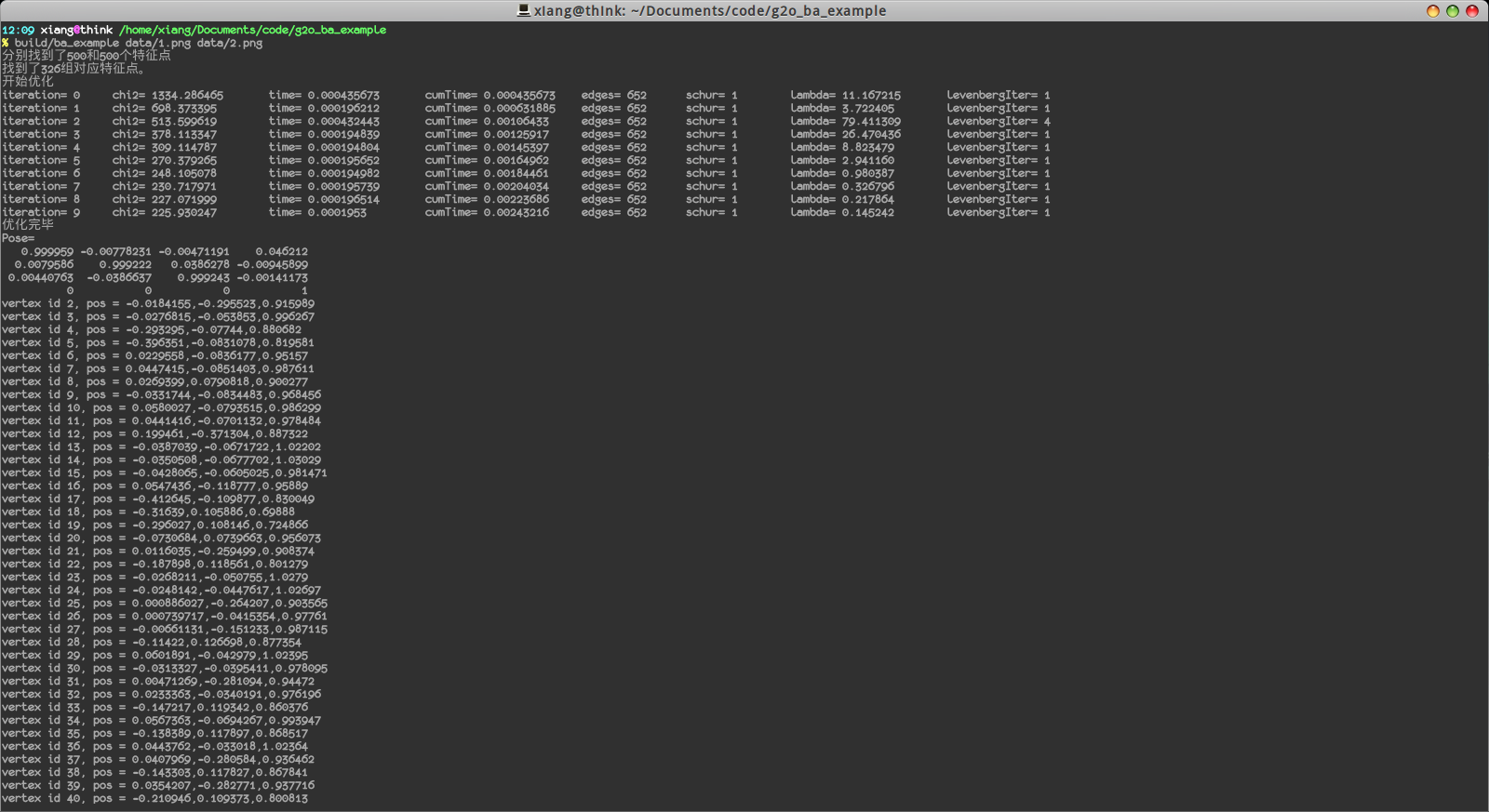
　　我们显示了特征点的数量，估计的位姿变换，以及各特征点的空间位置。最后，还显示了inliers的数量（我们把误差太大的边认为是outlier）：

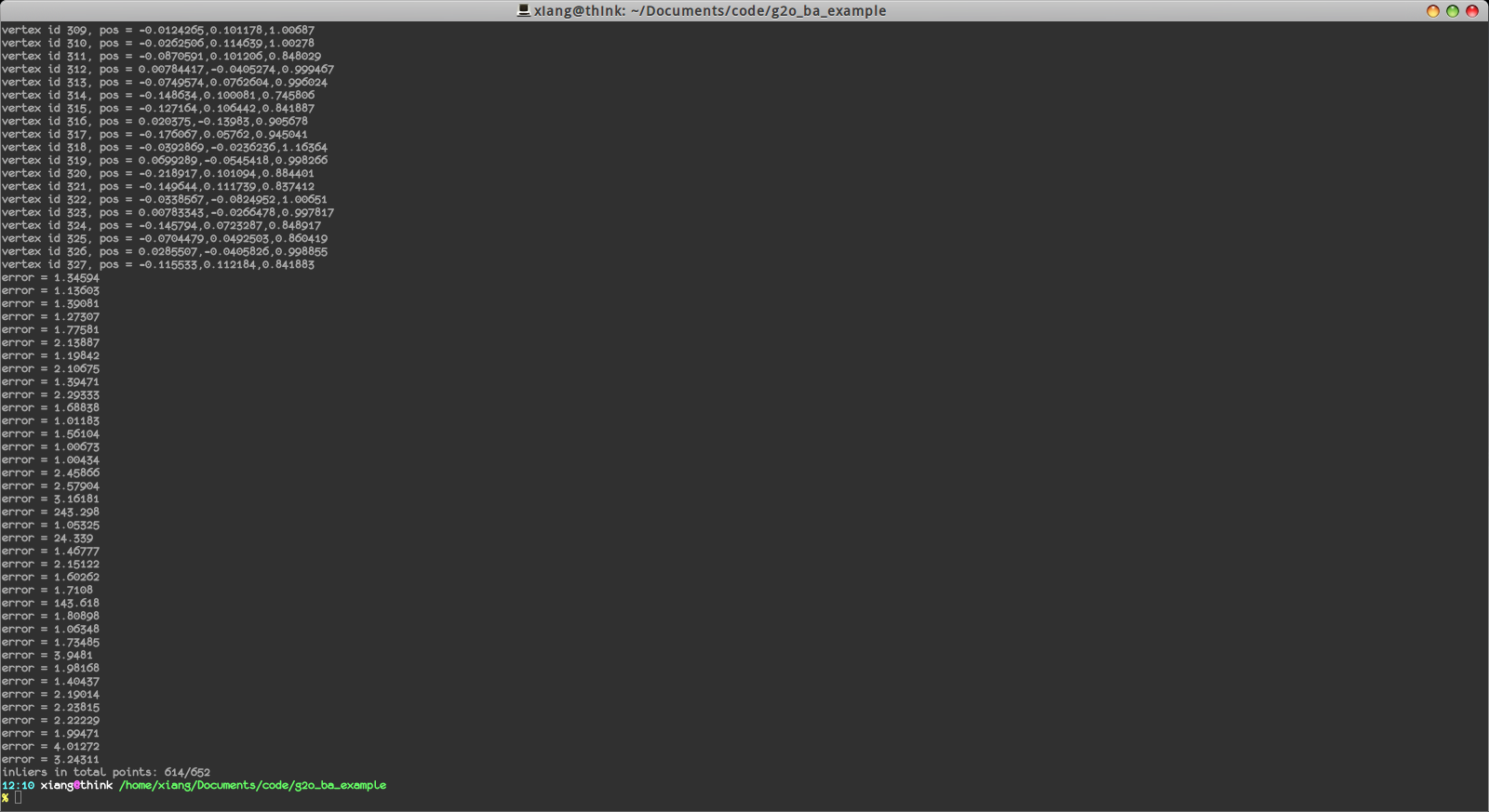
　　在652条边中有614条边是inlier，说明匹配还是挺正确的。

讨论

　　关于单目BA还有一点要说，就是 scale 不确定性。由于投影公式中的$\lambda$存在，我们只能推得一个相对的深度，而无法确切的知道特征点离我们有多少距离。如果我们把所有特征点的坐标放大一倍，把平移量$t$也乘以二，得到的结果是完全一样的。

　　比方说：看奥特曼时，我们并不知道这其实是人类演员在模型里打架。这就是单目带来的尺度不确定性。

　　小萝卜：师兄你现在才知道吗？我小时候就知道了啊！

小结

　　本节介绍了g2o的大致框架，并提供了一个计算单目双视图Bundle Adjustment的例程供读者练习。

　　如果你觉得我的博客有帮助，可以进行几块钱的小额赞助，帮助我把博客写得更好。