纪中9日T4 2298. 异或

2298. 异或

(File IO): input:gcdxor.in output:gcdxor.out

时间限制: 1000 ms  空间限制: 262144 KB  具体限制

题目描述

SarvaTathagata是个神仙，一天他在研究数论时，书上有这么一个问题：求不超过n两两的数的gcd。
SarvaTathagata这么神仙的人当然觉得这个是sb题啦。学习之余，他还发现gcd的某一个特别好的性质：如果有两个数i,j满足gcd(i,j)=i^j(这里的^为c++中的异或)的话，那么这两个数组成的数对(i,j)就是一个nb的数对(这里认为(i,j)和(j,i)为相同的，并不需要计算2次)。
当然，SarvaTathagata并不会只满足于判断一个数对是否nb，他还想知道满足两个数都是不超过n并且nb的数对有多少个。
由于SarvaTathagata实在是太神仙了，他认为这种题实在是太简单了。于是他找到了你，看看你是否能解决这个问题。

输入

共一行一个整数n，含义如题所述。

输出

一行一个整数，表示nb的数对的个数。

样例输入

样例输入1

12

样例输入2

123456

样例输出

样例输出1

8

样例输出2

214394

数据范围限制

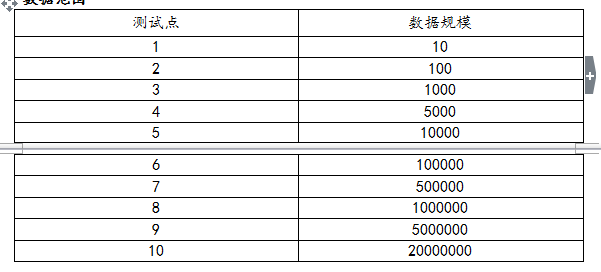
提示

样例1中共有八对，分别是：
{1,3},{1,5},{1,7},{1,9},{2,6},{1,11},{2,10},{4,12}。

提示有误，特此隐藏

---

Solution

这是一道数论题，涉及gcd，xor（^），二进制减法。

以上三者中，若你对任何一样过敏，请谨慎食用。

Way one（40分）

用个程序找规律

//gcdxor table
#include<bits/stdc++.h>
using namespace std;
int gcd(int ta,int tb)
{
    if(tb==) return ta;
    if(ta%!=&&tb%!=) return gcd(tb,ta%tb);
    if(ta%==&&tb%!=) return gcd(ta/,tb);
    if(ta%!=&&tb%==) return gcd(ta,tb/);
    return *gcd(ta/,tb/);
}

int ans[];
int n;
bool vis[],memory[][];//memory[i][j]
int search(int num)
{
    if(vis[num]) return ans[num];
    if(num==)
        return ; 

    vis[num]=;
    int now=;
    for(int i=;i<num;i++)
    {
        if(gcd(num,i)==(num xor i))
            now++;
//        if(gcd(i,num)==(i xor num))
//            now++;

    }
//    if(gcd(num,num)==(num xor num))
//        now++;
    ans[num]=ans[num-]+now;
    return ans[num];
}
int main()
{
    freopen("table4.txt","w",stdout);
    cin>>n;
//    int s=clock();
    int k;
    /*
    for(k=0;k<=n;k++)
    {
        if(k==0) {cout<<0<<endl;continue;}
        for(int i=1;i<=k;i++)
        {
            for(int j=1;j<=k;j++)
            {
                if(gcd(i,j)==(i xor j)){
                    memory[i][j]=true;
                    ans[k]++;

                }
//                cout<<memory[i][j]<<" ";
            }
//            cout<<endl;
        }

        cout<<k<<" "<<ans[k]/2<<endl;
    }
    */
//    /*
    for(int k=;k<=n;k++)
    {
        if(k==) {cout<<<<endl;continue;}
        cout<<k<<" "<<search(k)<<","<<endl;
    }
//    */
//    int e=clock();
//    cout<<e-s;

    return ;
}

可以无视我

找不到……

Code（40分）

#pragma GCC optimize(2)
#include<bits/stdc++.h>
#define IL inline
using namespace std;
short int diff[]{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,};
int n,ans;
IL int gcd(int ta,int tb)
{
    if(tb==) return ta;
    if(ta%!=&&tb%!=) return gcd(tb,ta%tb);
    if(ta%==&&tb%!=) return gcd(ta/,tb);
    if(ta%!=&&tb%==) return gcd(ta,tb/);
    return *gcd(ta/,tb/);
}
IL int search(int num)
{
    if(num==) {
        int t=;
        for(int i=;i<=;i++) t+=diff[i];
        return t;
    }
    int prev;
    if(num>)
        prev=search(num-);
    int now=;
    for(int i=;i<num;i++) if(gcd(num,i)==(num xor i)) now++;
    if(gcd(num,num)==(num xor num)) now++;
    return prev+now;
}
int main()
{
    freopen("gcdxor.in","r",stdin);
    freopen("gcdxor.out","w",stdout);
    cin>>n;
    for(int i=;i<=min(n,);i++)
        ans+=diff[i];
    if(n<=)
        cout<<ans<<endl;
    else
        cout<<search(n)<<endl;
    return ;
}

40分

其实，要是我愿意我可以把表全打出来，但是这个OJ有代码长度限制（5kb）。有毒……

Way two

从大神视角理解这道题：

看到gcd就去想数论嘛

求证：若gcd(a,b)=a xor b，则gcd(a,b)=a-b (a≥b)

转到完整证明

证明：

由更相减损法，可知gcd(a,b)=gcd(b,a-b)

这个的原理与辗转相除法类似，只是把求模换成了减法

若a-b=0，则gcd(a,b)=gcd(b,a-b)=a=b

否则a-b>0，此时gcd(a,b)=gcd(b,a-b)>a-b

所以，gcd(a,b)≥a-b

再分析xor运算和二进制减法

xor：对与每一位，若是相同则为0，若是不同则得1

1^1=0  1^0=1  0^1=1  0^0=0

减法：对于每一位，若是相同则得0，若是1 0则得1，若是0 1则得1并使上一位-1

1-1=0  1-0=1  0-1=-1  0-0=0

那么，如果两数a，b中出现了0->1的情况，则减法会使那一位上出现退位，异或（xor）则不会

所以，a xor b≥a-b

又因为（前面证明的）gcd(a,b)≥a-b

所以gcd(a,b)≥a-b≥a xor b

所以当gcd(a,b)=a xor b时，gcd(a,b)=a-b=a xor b

所以若gcd(a,b)=a xor b，则gcd(a,b)=a-b (a≥b)

证毕

回到此题

现在我已经证出来

若gcd(a,b)=a xor b，则gcd(a,b)=a-b (a≥b)

一看题目，就是当gcd(a,b)=a xor b时

那么我们就可以直接用结论了

设c=a-b，则b=a-c

若数对（a，b）符合条件

则c=a^b

故我只要枚举a和b即可！

Code（90分）

#pragma GCC optimize(2)//这个程序不开O2会超时（90分）
#include<bits/stdc++.h>
using namespace std;
int n,cnt[],sum[];
int main()
{
//    freopen("gcdxor.in","r",stdin);
//    freopen("gcdxor.out","w",stdout);
    cin>>n;
    memset(cnt, , sizeof(cnt));
    for(int c = ; c <= n; c++)
    for(int a = c*; a <= n; a += c) //因为a>=b，所以需要从2*c开始枚举
    {
        int b = a - c;
        if(c == (a ^ b)) cnt[a]++;//统计每个a对应的b的数量
    }//^的优先级低于==，所以要打上括号
    sum[] = ;
    for(int i = ; i <= n; i++)
        sum[i] = sum[i-] + cnt[i];
    cout<<sum[n];
    return ;
}

Code（100分）

#include<bits/stdc++.h>
using namespace std;
int n,sum;
int main()
{
//    freopen("gcdxor.in","r",stdin);
//    freopen("gcdxor.out","w",stdout);
    scanf("%d",&n);
//    int s=clock();
    for(int c=;c<=n;c++)//c=a-b
    for(int a=c*;a<=n;a+=c) //因为a>=b，所以需要从2*c开始枚举
        if(c==(a ^ (a-c))) sum++;
    //统计每个a对应的b的数量
    //^的优先级低于==，所以要打上括号
    printf("%d",sum);
//    int e=clock();
//    cout<<endl<<e-s;
    return ;
}

TLE？

细心的你应该发现这个：

不要怕TLE啦

如果你会算复杂度，会一点微积分，会一点金融学，你就要知道：

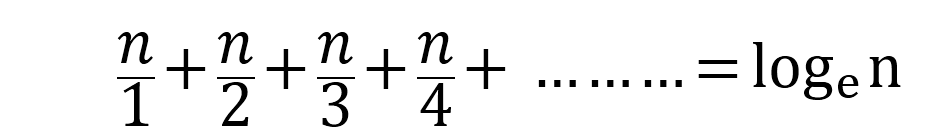
所以整个程序的时间复杂度为O（nlog（n））

Attention

一、^的优先级低于==，所以要打上括号

二、因为a>=b，所以需要从2*c开始枚举，使得a的最小值为2*c，b=a-c，b的初值值为c且越来越小

三、用前缀和的思想，递归sum[i] = sum[i-1] + cnt[i]，即n的答案是在n-1的基础上加上这次枚举的答案

END