大O表示法是什么？

1.什么是大O表示法:

1.在算法描述中，我们用这种方式来描述计算机算法的效率。
2.在计算机中，这种粗略的量度叫做 “大O” 表示法。
3.在具体的情境中，利用大O表示法来描述具体的快慢可能没有意义。
4.数据项发生变化时， 算法的效率会跟着发生变化。
5.所以我们通常使用一种 算法的速度 会如何跟随着 数据量的变化 的。

2.常见的大O表示法数值：

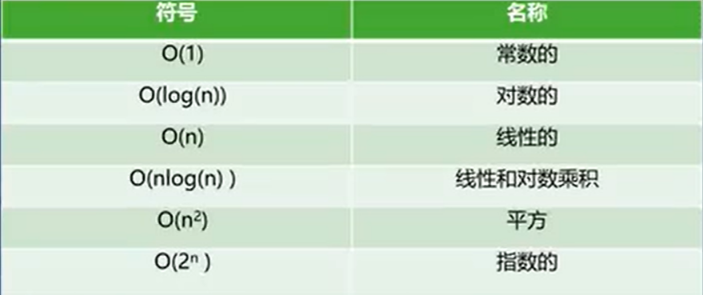
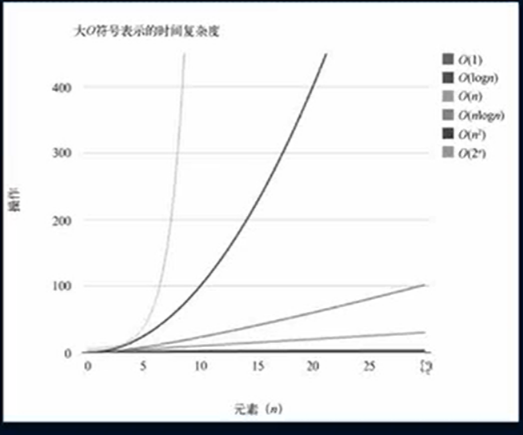
3.大O表示法推导的方式：

1.用常量1取代运行时间的加法常量。
2.再修改后的运行函数中，只保留最高项。
3.如果最高存在且不为1，则去除与这个项相乘的常数。