数据结构之递归Demo（走迷宫）（八皇后）（汉诺塔）

递归

顾名思义，递归就是递归就是递归就是递归就是递归......就是递归

　　Google递归：

　　

走迷宫（较容易）：

　　构建一个二维数组（如下图），其中1表示围墙，0表示通路，现要求从起点走到终点。利用递归可以以少量代码实现。

由于比较简单，直接上代码分析：

　　参数 i，j 为迷宫起始坐标，而要走出迷宫，必须绕过围墙1，走迷宫当然有策略，这里比较简单的给出了下右上左的次序判断是否通路，同样也可以上右下左，左上右下，左下右上，注意必须是闭环的，否则绝对走不出迷宫！（这里强烈建议按照代码自己思考走一遍或者debug分析一下）

 1 // 下右上左
 2     public static boolean setWay(int[][] array, int i, int j) {
 3         if (array[6][6] == 7)//判断每一种选择最后是否能走出迷宫
 4             return true;
 5         else {
 6             if (array[i][j] == 0) {
 7                 array[i][j] = 7;//表示此坐标已经来过，下面接着判断各种情况
 8                 if (setWay(array, i + 1, j))
 9                     return true;
10                 else if (setWay(array, i, j + 1))
11                     return true;
12                 else if (setWay(array, i - 1, j))
13                     return true;
14                 else if (setWay(array, i, j - 1))
15                     return true;
16                 else {
17                     array[i][j] = 3;
18                     return false;
19                 }
20             } else
21                 return false;
22         }
23     }

八皇后：

八皇后小游戏：  http://www.4399.com/baidugame/42643.htm    八皇后的规则很简单，但是实现不易，八皇后规定每一个皇后都必须在不同行不同列且不在一个对角线上。

这里给出92种摆法的一部分，感兴趣的朋友可以点击上面连接进行游戏测试

0 4 7 5 2 6 1 3
0 5 7 2 6 3 1 4
0 6 3 5 7 1 4 2
0 6 4 7 1 3 5 2
1 3 5 7 2 0 6 4

　　重点看一下这个分析图，用心一看，绝对明白了。

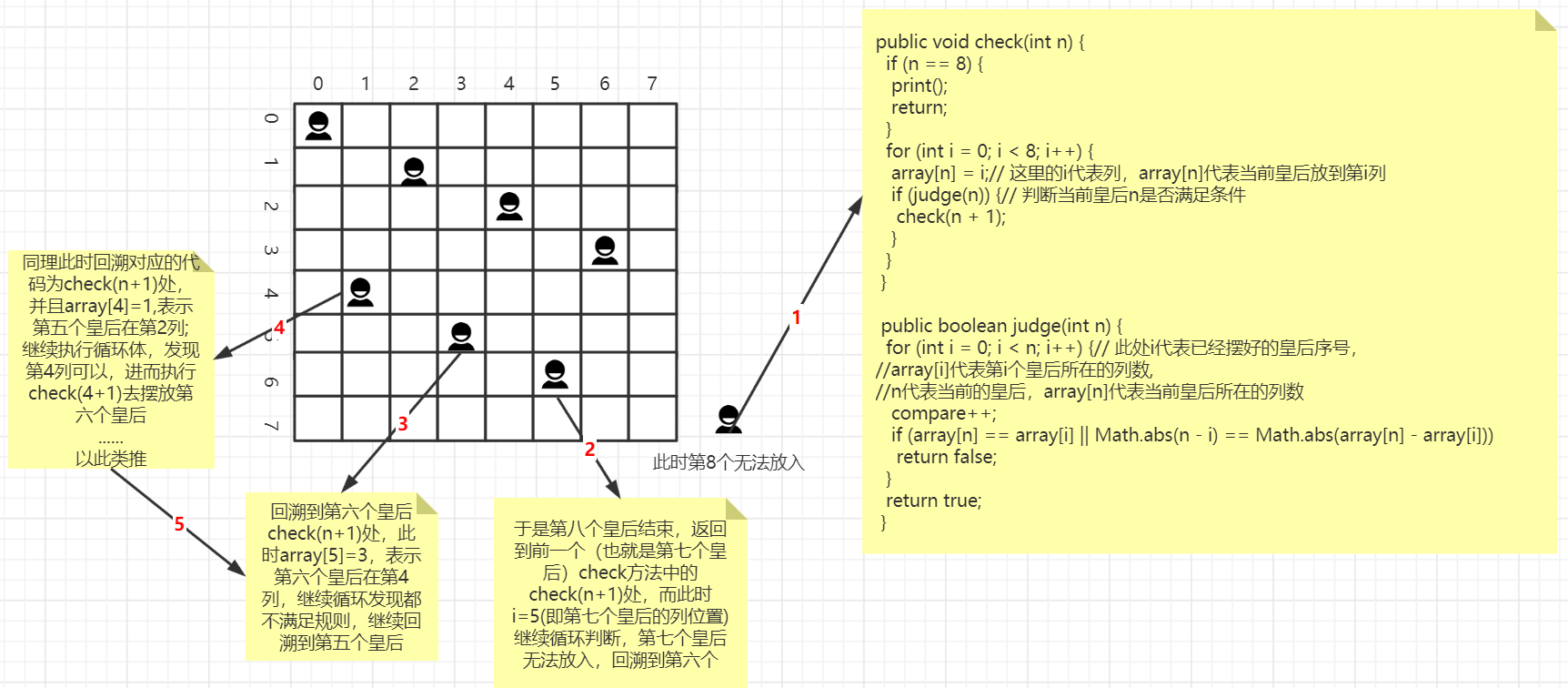
核心代码分析：

 1     public void check(int n) {
 2         if (n == max) {
 3             print();
 4             return;
 5         }
 6         for (int i = 0; i < max; i++) {
 7             array[n] = i;// 这里的i代表列，array[n]代表当前皇后放到第i列
 8             if (judge(n)) {// 判断当前皇后n是否满足条件
 9                 check(n + 1);//满足条件，判断下一个皇后
10             }
11         }
12     }
13
14     //此方法主要判断当前皇后能否摆放
15     public boolean judge(int n) {
16         for (int i = 0; i < n; i++) {// 此处i代表已经摆好的皇后序号，array[i]代表第i个皇后所在的列数, n代表当前的皇后，array[n]代表当前皇后所在的列数
17             //将当前第n个皇后的列array[n]和前n个皇后的列进行比较，还有斜率比较
18             if (array[n] == array[i] || Math.abs(n - i) == Math.abs(array[n] - array[i]))
19                 return false;
20         }
21         return true;
22     }

汉诺塔（分治法）：

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

　　假如按照上面规则去移动，一秒移动一次，那么这表明移完这些金片需要5845.42亿年以上，而地球存在至今不过45亿年，太阳系的预期寿命据说也就是数百亿年。

 

为什么呢？基本过程看图：类似有规则的搭积木。

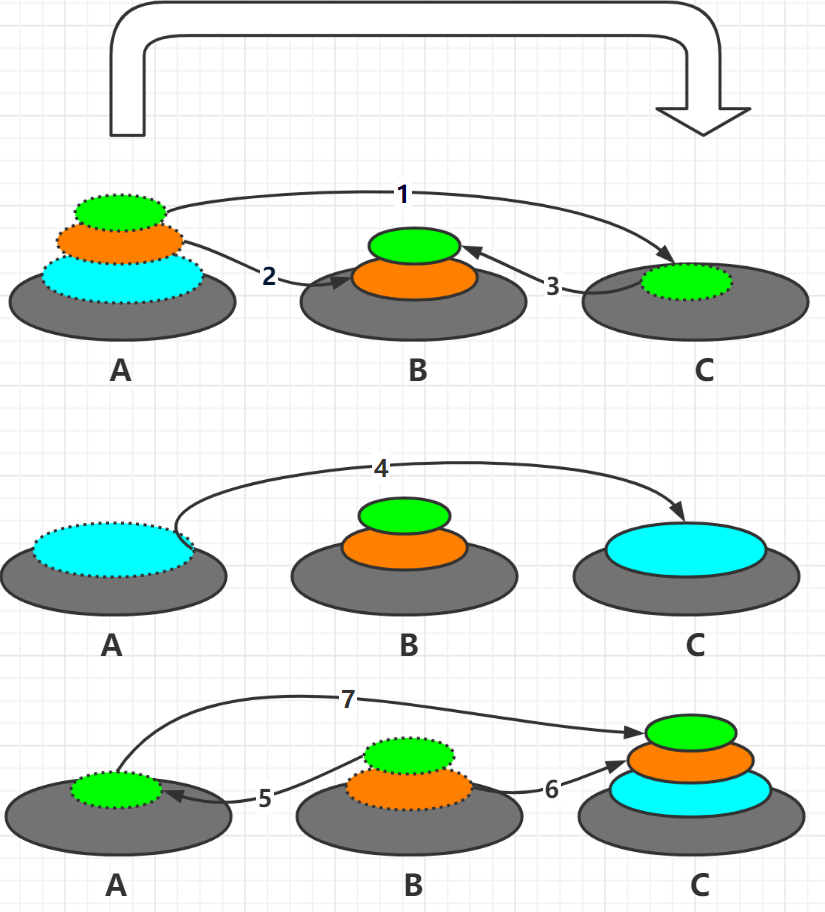
　　 以上示图分析，以3片为例，一共需要移动7次。

　　 思路分析：将所有片看作两部分，最底下一片和上面所有片；接着将上面所有片分为两部分，最底下一片和上面所有片......

　　　　　　　 1、将所有上层片，从A放到B位置上

　　　　　　　 2、然后剩余最底下的一片，从A放到C位置上

　　　　　　　 3、接着将B盘中所有片放到C位置上

　　 以上是宏观上的步骤，而真正移动是在回溯的时候。用图说明一下：

　　 方法在执行的时候是按照栈帧执行的，下面也就是模拟了一遍3片的执行过程。

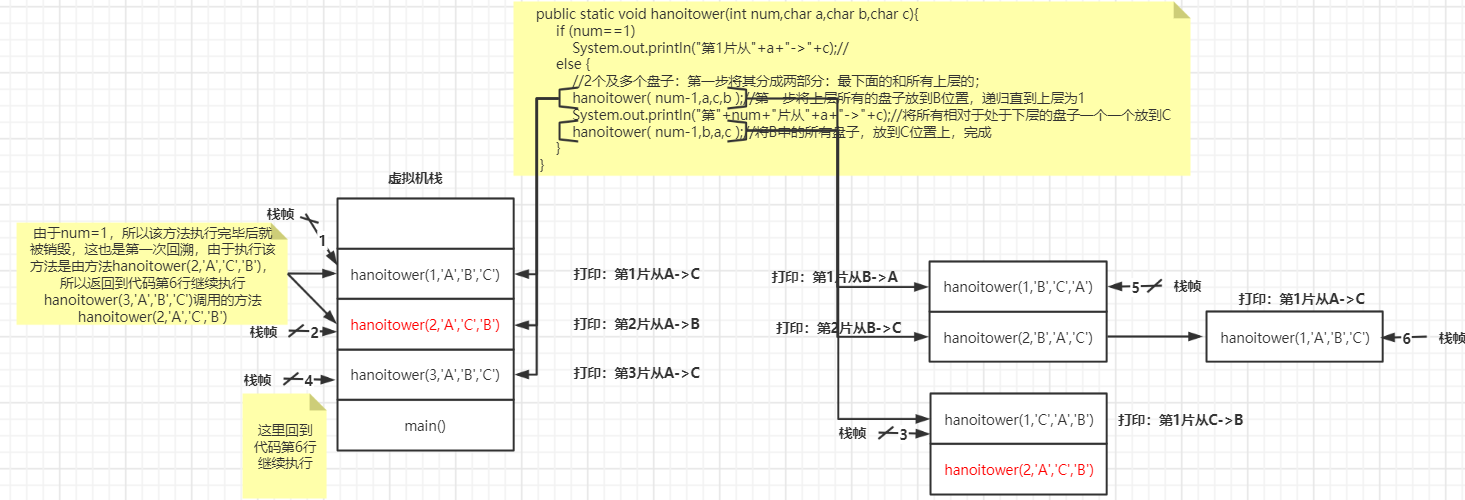
 1   //参数说明：num表示有多少片，abc依次表示三个容器
 2   public static void hanoitower(int num,char a,char b,char c){
 3         if (num==1)
 4             System.out.println("第1个盘从"+a+"->"+c);//
 5         else {
 6             //2个及多个盘子：第一步将其分成两部分：最下面的和所有上层的；
 7             hanoitower( num-1,a,c,b );//第一步将上层所有的盘子放到B位置，递归直到上层为1
 8             System.out.println("第"+num+"个盘从"+a+"->"+c);//将所有相对于处于下层的盘子一个一个放到C
 9             hanoitower( num-1,b,a,c );//将B中的所有盘子，放到C位置上，完成
10         }
11     }