通过CGAL将一个多边形剖分成Delaunay三角网

目录

• 1. 概述
• 2. 实现
• 3. 结果
• 4. 参考

1. 概述

对于平面上的点集，通过Delaunay三角剖分算法能够构建一个具有空圆特性和最大化最小角特性的三角网。空圆特性其实就是对于两个共边的三角形，任意一个三角形的外接圆中都不能包含有另一个三角形的顶点，这种形式的剖分产生的最小角最大。

更进一步的，可以给Delaunay三角网加入一些线段的约束条件，使得构建的Delaunay三角网能够利用这些线段。利用这个特性，可以将一个多边形剖分成Delaunay三角网，开源工具CGAL就正好提供了这个功能。

2. 实现

因为要显示三角网的效果，所以我在《使用QT绘制一个多边形》这篇博文提供的QT界面上进行修改，正好这篇文章提供的代码还实现了在QT中绘制多边形的功能。

关于网格化以及三角网剖分，在CGAL中提供了非常详尽繁复的解决方案，我这里选择了CGAL::refine_Delaunay_mesh_2这个接口，这个接口能够将多边形区域构建成一个Delaunay三角网，如果当前的存在三角形不满足Delaunay，就会在其中补充一些点来满足Delaunay的相关特性。主要的实现代码如下(具体代码见文章最后)：

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Constrained_Delaunay_triangulation_2.h>
#include <CGAL/Delaunay_mesher_2.h>
#include <CGAL/Delaunay_mesh_face_base_2.h>
#include <CGAL/Delaunay_mesh_size_criteria_2.h>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Triangulation_vertex_base_2<K> Vb;
typedef CGAL::Delaunay_mesh_face_base_2<K> Fb;
typedef CGAL::Triangulation_data_structure_2<Vb, Fb> Tds;
typedef CGAL::Constrained_Delaunay_triangulation_2<K, Tds> CDT;
typedef CGAL::Delaunay_mesh_size_criteria_2<CDT> Criteria;
typedef CDT::Vertex_handle Vertex_handle;
typedef CDT::Point Point;

//三角化
void GraphicsPainter::Triangulate()
{
    //找到边界上所有的像素点
    vector<Vector2d> ROIBoundPointList;
    CalBoundPoint(ROIBoundPointList);

    CDT cdt;
    vector<Vertex_handle> vertexList;
    cout<<ROIBoundPointList.size()<<endl;
//    for(int i = 0; i<pointList.size(); i++)
//    {
//        vertexList.push_back(cdt.insert(Point(pointList[i].x(), pointList[i].y() )));
//    }
    for(int i = 0; i<ROIBoundPointList.size(); i++)
    {
        vertexList.push_back(cdt.insert(Point(ROIBoundPointList[i].x, ROIBoundPointList[i].y )));
    }

    for(unsigned int i =0;i<vertexList.size()-1;i++)
    {
        cdt.insert_constraint(vertexList[i],vertexList[i+1]);
    }
    //cdt.insert_constraint(vertexList[vertexList.size()-1],vertexList[0]);

    std::cout << "Number of vertices: " << cdt.number_of_vertices() <<std::endl;
    std::cout << "Meshing the triangulation..." << std::endl;

    CGAL::refine_Delaunay_mesh_2(cdt, Criteria());
    std::cout << "Number of vertices: " << cdt.number_of_vertices() <<std::endl;

    CDT::Face_iterator fit;
    for (fit = cdt.faces_begin(); fit!= cdt.faces_end(); ++fit)
    {
        QVector<QPointF> triPoint;
        triPoint.push_back(QPointF(fit->vertex(0)->point().x(), fit->vertex(0)->point().y()));
        triPoint.push_back(QPointF(fit->vertex(1)->point().x(), fit->vertex(1)->point().y()));
        triPoint.push_back(QPointF(fit->vertex(2)->point().x(), fit->vertex(2)->point().y()));
        QPolygonF tri(triPoint);
        triList.push_back(tri);
    }

    bTri = true;
    update();
}

3. 结果

在QT界面上绘制一个多边形，只用多边形上的点，最后的三角网格效果：

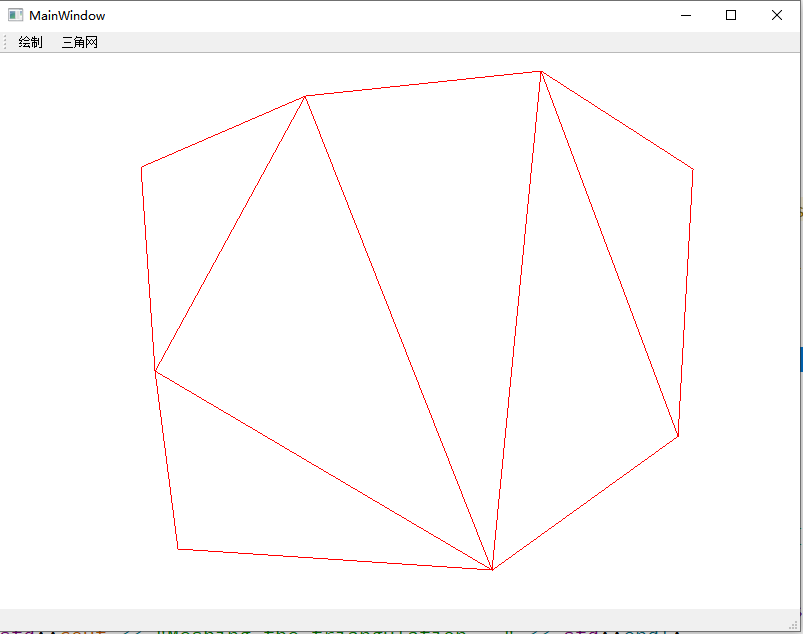
通过这篇博文《矢量线的一种栅格化算法》提供的栅格化算法，可以将一个多边形栅格化，这样就可以得到一个栅格多边形，通过这个算法网格化，最后的效果：

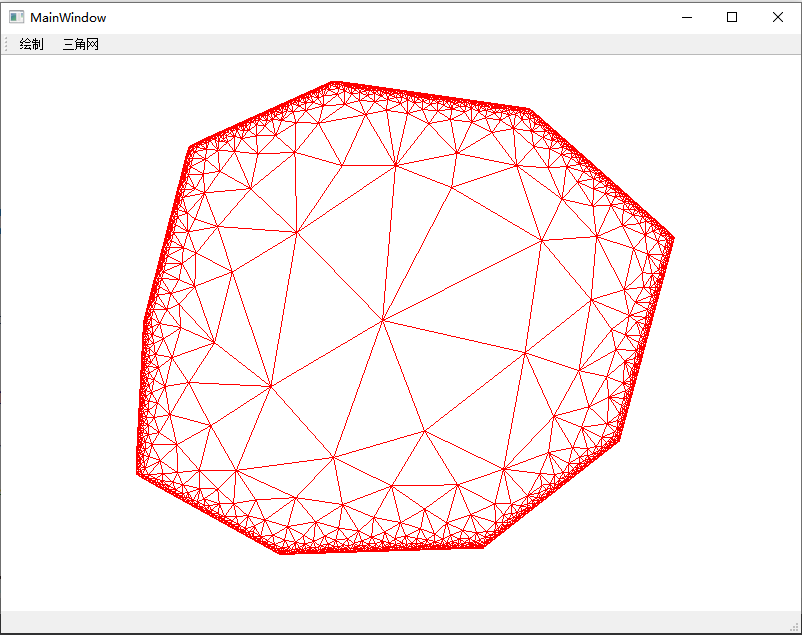
可以发现这种方式会在内部新添加一些点，来满足Delaunay特性。并且会形成边界密集，中间稀疏的网格效果。在一些图形、图像处理中，会用到这种自适应网格（Adaptive Mesh）。

4. 参考

1. Delaunay三角剖分学习笔记

实现代码