最小生成树POJ3522 Slim Span[kruskal]

Slim Span

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 7594		Accepted: 4029

Description

Given an undirected weighted graph G, you should find one of spanning trees specified as follows.

The graph G is an ordered pair (V, E), where V is a set of vertices {v₁, v₂, …, v_n} and E is a set of undirected edges {e₁, e₂, …, e_m}. Each edge e ∈ E has its weight w(e).

A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n − 1 edges. The slimness of a spanning tree T is defined as the difference between the largest weight and the smallest weight among the n − 1 edges of T.

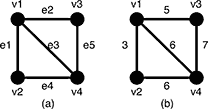
Figure 5: A graph G and the weights of the edges

For example, a graph G in Figure 5(a) has four vertices {v₁, v₂, v₃, v₄} and five undirected edges {e₁, e₂, e₃, e₄, e₅}. The weights of the edges are w(e₁) = 3, w(e₂) = 5, w(e₃) = 6, w(e₄) = 6, w(e₅) = 7 as shown in Figure 5(b).

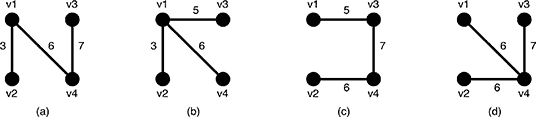
Figure 6: Examples of the spanning trees of G

There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning tree T_a in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the tree T_a is 4. The slimnesses of spanning trees T_b, T_c and T_d shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1.

Your job is to write a program that computes the smallest slimness.

Input

The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.

n	m
a1	b1	w1
	⋮
am	bm	wm

Every input item in a dataset is a non-negative integer. Items in a line are separated by a space. n is the number of the vertices and m the number of the edges. You can assume 2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2. a_k and b_k(k = 1, …, m) are positive integers less than or equal to n, which represent the two vertices v_ak and v_bk connected by the kth edge e_k. w_k is a positive integer less than or equal to 10000, which indicates the weight of e_k. You can assume that the graph G = (V, E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices).

Output

For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, −1 should be printed. An output should not contain extra characters.

Sample Input

4 5
1 2 3
1 3 5
1 4 6
2 4 6
3 4 7
4 6
1 2 10
1 3 100
1 4 90
2 3 20
2 4 80
3 4 40
2 1
1 2 1
3 0
3 1
1 2 1
3 3
1 2 2
2 3 5
1 3 6
5 10
1 2 110
1 3 120
1 4 130
1 5 120
2 3 110
2 4 120
2 5 130
3 4 120
3 5 110
4 5 120
5 10
1 2 9384
1 3 887
1 4 2778
1 5 6916
2 3 7794
2 4 8336
2 5 5387
3 4 493
3 5 6650
4 5 1422
5 8
1 2 1
2 3 100
3 4 100
4 5 100
1 5 50
2 5 50
3 5 50
4 1 150
0 0

Sample Output

1
20
0
-1
-1
1
0
1686
50

Source

Japan 2007

---

copy一下MST的性质：

• (1)切割性质：（各边边权均不相同）一条边是连接图中某非全集非空集的点集合S和其补集中所有的边的最小边，那么这条边就在最小生成树中。
• 证明：回忆kruscal算法的过程，这条边是连接这两个集合的最小边，那么在枚举到这条边之前，这两个集合一定没有被合并

• (2)回路性质：（各边边权均不相同）图若有回路，那么回路中的最长边一定不在最小生成树中
• 证明：回路中至少一条边不在最少生成树中，假设最长边在最小生成树中，那么一定存在一条更小的边替代它。

• (3)最小瓶颈生成树：使最大边权值尽量小的生成树
• 最小生成树就是这么一棵树，因为kruscal算法的过程
• (4)最小瓶颈路：找u到v的一条路径满足最大边权值尽量小
• 先求最小生成树，然后u到v的路径在树上是唯一的，答案就是这条路径
• 如果只求一次，也可以用spfa稍作变形解决

本题求最苗条的生成树

可以发现对于一个最小边的权值，它对应的MST中的最大边的权值一定是最苗条的

枚举求就可以了

//
//  main.cpp
//  poj3522slim
//
//  Created by Candy on 9/14/16.
//  Copyright © 2016 Candy. All rights reserved.
//

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=,INF=1e9;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x;
}
int n,m,ans=INF;
struct edge{
    int u,v,w;
    bool operator<(const edge &rhs)const{return w<rhs.w;}
}e[N*N];
int p[N];
int find(int x){return x==p[x]?x:p[x]=find(p[x]);}
int kruskal(int st){
    int ans=INF,cnt=;
    for(int i=;i<=n;i++) p[i]=i;
    for(int i=st;i<=m;i++){
        int u=e[i].u,v=e[i].v;
        int x=find(u),y=find(v);
        if(x!=y){
            ans=e[i].w;
            p[x]=y;
            if(++cnt==n-) break;
        }
    }
    if(cnt!=n-) return -;
    return ans;
}
int main(int argc, const char * argv[]) {
    while(cin>>n>>m){
        if(n==&&m==) break;
        ans=INF;
        for(int i=;i<=m;i++){
            e[i].u=read();e[i].v=read();e[i].w=read();
        }
        sort(e+,e++m);
        for(int st=;st<=m-n+;st++){
            int tmp=kruskal(st);
            if(tmp!=-) ans=min(ans,tmp-e[st].w);
        }
        if(ans!=INF) printf("%d\n",ans);
        else printf("-1\n");
    }
    return ;
}