降维处理PCA
- 数据在低维下更容易处理、更容易使用;
- 相关特征,特别是重要特征更能在数据中明确的显示出来;如果只有两维或者三维的话,更便于可视化展示;
- 去除数据噪声
- 降低算法开销
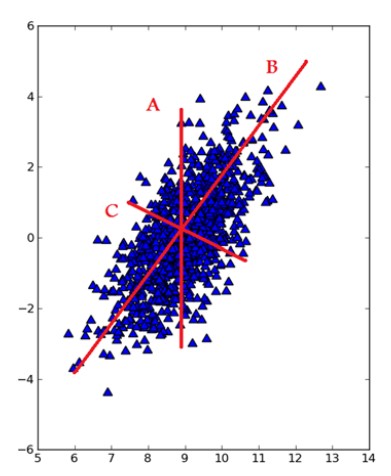
去除平均值计算协方差矩阵计算协方差矩阵的特征值和特征向量将特征值从大到小排序保留最上面的N个特征向量将数据转换到上述N个特征向量构建的新空间中
# 加载数据的函数def loadData(filename, delim = '\t'):fr = open(filename)stringArr = [line.strip().split(delim) for line in fr.readlines()]datArr = [map(float,line) for line in stringArr]return mat(datArr)# =================================# 输入:dataMat:数据集# topNfeat:可选参数,需要应用的N个特征,可以指定,不指定的话就会返回全部特征# 输出:降维之后的数据和重构之后的数据# =================================def pca(dataMat, topNfeat=9999999):meanVals = mean(dataMat, axis=0)# axis = 0表示计算纵轴meanRemoved = dataMat - meanVals #remove meancovMat = cov(meanRemoved, rowvar=0)# 计算协方差矩阵eigVals,eigVects = linalg.eig(mat(covMat))# 计算特征值(eigenvalue)和特征向量eigValInd = argsort(eigVals) #sort, sort goes smallest to largesteigValInd = eigValInd[:-(topNfeat+1):-1] #cut off unwanted dimensionsredEigVects = eigVects[:,eigValInd] #reorganize eig vects largest to smallestlowDDataMat = meanRemoved * redEigVects#transform data into new dimensionsreconMat = (lowDDataMat * redEigVects.T) + meanValsreturn lowDDataMat, reconMat
filename = r'E:\ml\machinelearninginaction\Ch13\testSet.txt'dataMat = loadData(filename)lowD, reconM = pca(dataMat, 1)
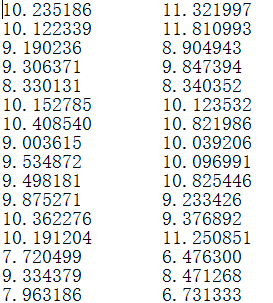
def plotData(dataMat,reconMat):fig = plt.figure()ax = fig.add_subplot(111)# 绘制原始数据ax.scatter(dataMat[:, 0].flatten().A[0], dataMat[:,1].flatten().A[0], marker='^', s = 90)# 绘制重构后的数据ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0], marker='o', s = 10, c='red')plt.show()
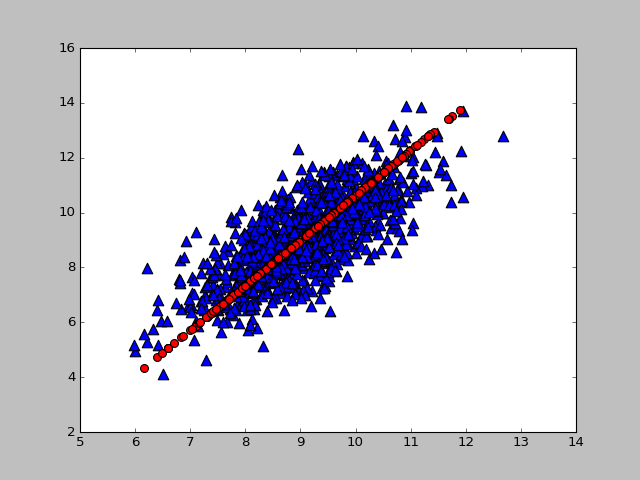
lowD, reconM = pca(dataMat, 2)
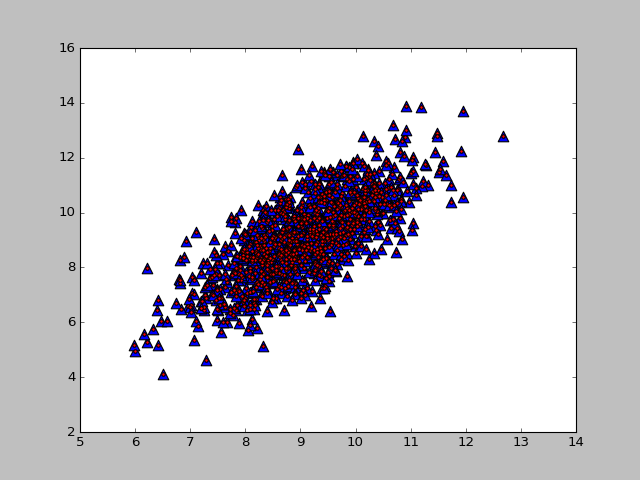
降维处理PCA的更多相关文章
- 机器学习基础与实践(三)----数据降维之PCA
写在前面:本来这篇应该是上周四更新,但是上周四写了一篇深度学习的反向传播法的过程,就推迟更新了.本来想参考PRML来写,但是发现里面涉及到比较多的数学知识,写出来可能不好理解,我决定还是用最通俗的方法 ...
- 降维技术---PCA
数据计算和结果展示一直是数据挖掘领域的难点,一般情况下,数据都拥有超过三维,维数越多,处理上就越吃力.所以,采用降维技术对数据进行简化一直是数据挖掘工作者感兴趣的方向. 对数据进行简化的好处:使得数据 ...
- 降维之pca算法
pca算法: 算法原理: pca利用的两个维度之间的关系和协方差成正比,协方差为0时,表示这两个维度无关,如果协方差越大这表明两个维度之间相关性越大,因而降维的时候, 都是找协方差最大的. 将XX中的 ...
- 降维【PCA & SVD】
PCA(principle component analysis)主成分分析 理论依据 最大方差理论 最小平方误差理论 一.最大方差理论(白面机器学习) 对一个矩阵进行降维,我们希望降维之后的每一维数 ...
- 机器学习算法总结(九)——降维(SVD, PCA)
降维是机器学习中很重要的一种思想.在机器学习中经常会碰到一些高维的数据集,而在高维数据情形下会出现数据样本稀疏,距离计算等困难,这类问题是所有机器学习方法共同面临的严重问题,称之为“ 维度灾难 ”.另 ...
- 降维方法PCA与SVD的联系与区别
在遇到维度灾难的时候,作为数据处理者们最先想到的降维方法一定是SVD(奇异值分解)和PCA(主成分分析). 两者的原理在各种算法和机器学习的书籍中都有介绍,两者之间也有着某种千丝万缕的联系.本文在简单 ...
- ML: 降维算法-PCA
PCA (Principal Component Analysis) 主成份分析 也称为卡尔胡宁-勒夫变换(Karhunen-Loeve Transform),是一种用于探索高维数据结 ...
- 特征降维之PCA
目录 PCA思想 问题形式化表述 PCA之协方差矩阵 协方差定义 矩阵-特征值 PCA运算步骤 PCA理论解释 最大方差理论 性质 参数k的选取 数据重建 主观理解 应用 代码示例 PCA思想 PCA ...
- 机器学习之路:python 特征降维 主成分分析 PCA
主成分分析: 降低特征维度的方法. 不会抛弃某一列特征, 而是利用线性代数的计算,将某一维度特征投影到其他维度上去, 尽量小的损失被投影的维度特征 api使用: estimator = PCA(n_c ...
- 降维算法-PCA主成分分析
1.PCA算法介绍主成分分析(Principal Components Analysis),简称PCA,是一种数据降维技术,用于数据预处理.一般我们获取的原始数据维度都很高,比如1000个特征,在这1 ...
随机推荐
- spring boot -- 配置文件application.properties 换成 application.yml
1.前言 其实两种配置文件在spring boot 的作用一样,只是写法不同 ,yml 可以写的内容更少 ,以树结构 书写内容,看起来很清晰, 但是 如果 项目配置文件设置为 既有properties ...
- react中使用antd按需加载(第一部)
什么是react按需加载?简单来说就是当我们引用antd的时候需要引入全局css样式,这会对性能造成一定的影响,那么使用按需加载以后就不需要引入css全局样式了,直接引入功能模块即可,既然需要设置按需 ...
- 遍历hashmap的6种方法
1. 通过ForEach循环进行遍历 mport java.io.IOException; import java.util.HashMap; import java.util.Map; public ...
- 帮你克服web字体选择焦虑症
1.背景 前端时间产品经理问我,移动端web默认字体有哪些,哪些字体不侵权?我当时感觉这方面的知识很匮乏,只能回答出微软雅黑和苹方简体,平常写代码时,没怎么留意过font-family设置的字体属性, ...
- 51 Nod 1134 最长递增子序列 (动态规划基础)
原题链接:1134 最长递增子序列 题目分析:长度为 的数列 有多达 个子序列,但我们应用动态规划法仍可以很高效地求出最长递增子序列().这里介绍两种方法. 先考虑用下列变量设计动态规划的算法. ...
- 《Flink SQL任务自动生成与提交》后续:修改flink源码实现kafka connector BatchMode
目录 问题 思路 kafka参数问题 支持batchmode的问题 参数提交至kafkasource的问题 group by支持问题 实现 编译 测试 因为在一篇博文上看到介绍"汽车之家介绍 ...
- Android官方文档翻译 三 1.1Creating an Android Project
Creating an Android Project 创建一个Android项目 An Android project contains all the files that comprise th ...
- linux 查看端口占用情况并关闭进程
首先要搞清楚 linux 查看进程和查看端口是两个概念,一般来讲进程会有多个,而固定端口只会有一个. 1.查看进程 ,通常在使用 ps 命令后 用管道连接(ps -ef|grep xxx ) 查 ...
- android ndk下没有pthread_yield,好在std::this_thread::yield()可以达到同样的效果
一个多线程的算法中,发现线程利用率只有47%左右,大量的处理时间因为usleep(500)而导致线程睡眠: 性能始终上不去. 把usleep(500)修改为std::this_thread::yiel ...
- Anchor CMS 0.12.7 跨站请求伪造漏洞(CVE-2020-23342)
这个漏洞复现相对来说很简单,而且这个Anchor CMS也十分适合新手训练代码审计能力.里面是一个php框架的轻量级设计,通过路由实现的传递参数. 0x00 漏洞介绍 Anchor(CMS)是一款优秀 ...
