GoogLeNet 改进之 Inception-v2/v3 解读

博主在前一篇博客中介绍了GoogLeNet 之 Inception-v1 解读中的结构和思想。Inception的计算成本也远低于VGGNet。然而，Inception架构的复杂性使得更难以对网络进行更改。如果单纯地放大架构，大部分的计算收益可能会立即丢失。这通过大量使用降维和Inception模块的并行结构来实现，这允许减轻结构变化对邻近组件的影响。但是，对于这样做需要谨慎，因为应该遵守一些指导原则来保持模型的高质量。

1 基本原则

• 要防止出现特征描述的瓶颈（representational bottleneck）。所谓特征描述的瓶颈就是中间某层对特征在空间维度进行较大比例的压缩（比如使用pooling时），导致很多特征丢失。虽然Pooling是CNN结构中必须的功能，但我们可以通过一些优化方法来减少Pooling造成的损失。
• 特征的数目越多收敛的越快。相互独立的特征越多，输入的信息就被分解的越彻底，分解的子特征间相关性低，子特征内部相关性高，把相关性强的聚集在了一起会更容易收敛。这点就是Hebbin原理：fire together, wire together。

第一点和第二点可以在一起解读，特征越多能加快收敛速度，但是无法弥补Pooling造成的特征损失。

• 空间聚合可以在较低维度嵌入上完成，而不会在表示能力上造成许多或任何损失。例如，在执行更多展开（例如3×3）卷积之前，可以在空间聚合之前减小输入表示的维度，没有预期的严重不利影响。
• 平衡网络的宽度和深度。通过平衡每个阶段的滤波器数量和网络的深度可以达到网络的最佳性能。增加网络的宽度和深度可以有助于更高质量的网络。

2 优化方法

2.1 基于大滤波器尺寸分解卷积

可以将大尺度的卷积分解成多个小尺度的卷积来减少计算量。比如将1个5x5的卷积分解成两个3x3的卷积串联。如下图所示：

假设5x5和两级3x3卷积输出的特征数相同，那两级3x3卷积的计算量就是前者的 (3x3+3x3)/5x5=18/25

2.2 空间分解为不对称卷积

在2.1中我们可以判断，大于3x3的卷积都可以分解成3x3的卷积，我们继续考虑可否分解成更小的？

可以使用非对称卷积。将nxn的卷积分解成1xn和nx1卷积的串联，例如n=3，分解后就能节省33%的计算量。相比之下，将3×3卷积分解为两个2×2卷积表示仅节省了11％的计算量。博主自己测试后发现在网络结构的中间层级（在m×m特征图上，其中m范围在12到20之间）的时候取得的效果比较好。如下图所示：

2.3 利用辅助分类器

引入了辅助分类器的概念，以改善非常深的网络的收敛。最初的动机是将有用的梯度推向较低层，使其立即有用，并通过抵抗非常深的网络中的消失梯度问题来提高训练过程中的收敛。辅助分类器还起着正则化项的作用。这是由于如果侧分支是批标准化的[7]或具有丢弃层，则网络的主分类器性能更好。这也为推测批标准化作为正则化项给出了一个弱支持证据。

当然原文作者在论文中提到输入侧的那个Auxiliary Classifier，加不加完全没区别，但如果在靠近输出的那个Auxiliary Classifier的全连接层后加个BN，会起到正则化的作用，所有 第二个Auxiliary Classifier还是可以保留。

2.4 使用并行结构

基本原则的第一点提到了使用 Pooling 会造成 represtation bottleneck，即特征的丢失。

一种解决办法就是在Pooling前用1x1卷积把特征数加倍（下图右图）这种加倍可以理解加入了冗余的特征，然后再作Pooling就只是把冗余的信息重新去掉，没有减少信息量。这种方法有很好的效果但因为加入了1x1卷积会极大的增大计算量。

比如，

另一方法是使用两个并行的支路，一路1x1卷积，由于特征维度没有加倍计算量相比之前减少了一倍，一路是Pooling，最后再在特征维度拼合到一起（如下图）。这种方法即有很好的效果，又没有增大计算量。使用两个平行的步长为2的块：PP和CC。PP是一个池化层（平均池化或最大池化）的激活，两者都是步长为2。

2.5 Label Smoothing来对网络输出进行正则化

Softmax层的输出如下公式：

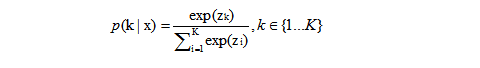
zi是对数单位或未归一化的对数概率。

loss为下面公式：

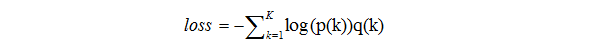
假设分类的标签是独热码表示(正确分类是1，其他类别是0)，从公式4可以反推出整个训练过程收敛时Softmax的正确分类的输入Zk是无穷大，这是一种极其理想的情况。这样就会过拟合。

为了克服过拟合，在输出p(k)时加了个参数delta，生成新的q'(k)，再用它替换上面公式中的q(k)来计算loss，如下：

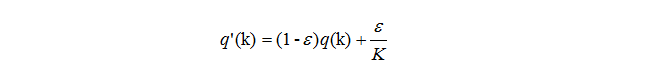
3 Inception-v1/v2 的具体结构

把上述优化方法组合到一起，就有了 Inceptio-v2 结构，如下表：

表中的 Inception 模块如下图：

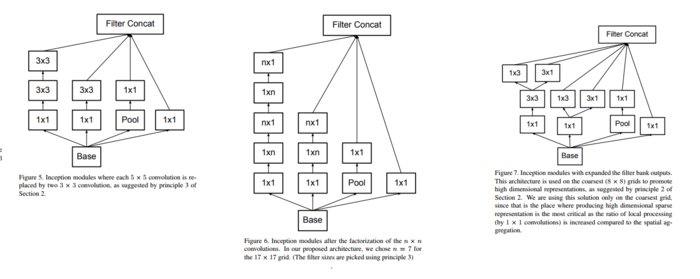
(左)第一级inception结构 (中)第二级inception结构 (右)第三级inception结构

在 Inceptio-v2 结构的基础上增加辅助分类器和 BN 就成为了Inception-v3。

参考资料：

https://arxiv.org/abs/1512.00567

https://zhuanlan.zhihu.com/p/32702113