图的封装（C++）

一. 问题说明

1.问题的简单描述

将图和网的的创建和基本操作分封装到class

用来熟悉此种数据结构和基于这种数据结构上的基本算法

采用VS2010编译环境

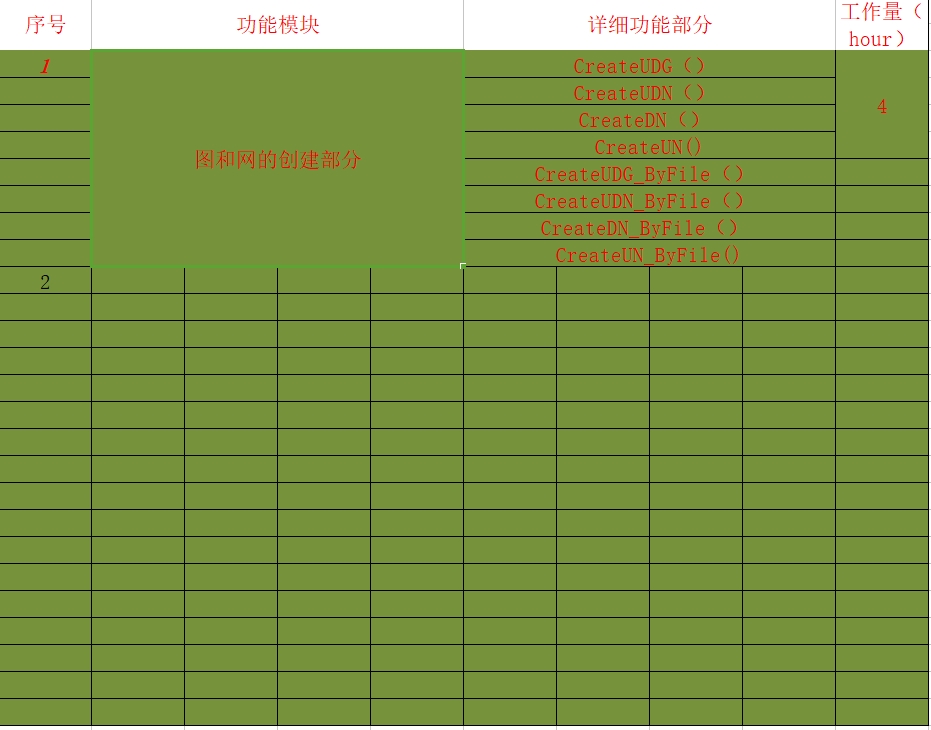
2.工作安排

二. 源代码

1.文件stdafx.h

 #pragma once
 #include "targetver.h"
 #include <stdio.h>
 #include <tchar.h>
 #include<iostream>
 #include<string>
 #include<string.h>
 using namespace std;
 /*
     以下完成图的存储结构
     (
         关键在于结构体的组合
     )
 */
 #define INFINITY   INT_MAX // 用整形最大值代替∞
 const int MAX_VERTEX_NUM=;// 最大顶点个数
 #define VRType  int  //顶点关系类型
 #define InfoType  string//弧相关信息
 #define VertexType string//顶点类型
 enum GraphKind{DG,DN,UDG,UDN};// 有向图，有向网，无向图，无向网
 typedef struct
 {
     VRType  adj; //adjacency  邻接
                  // 对图来说1(是)，0(否)表示相邻关系
                  // 对网来说为权值
     InfoType info;   //Info 信息
                       //该弧相关信息的指针
 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
       //Arc  弧（边）
 struct MGraph
 {
     VertexType vex[MAX_VERTEX_NUM];   //顶点向量
     AdjMatrix arcs;   //邻接矩阵
     int vexnum,arcnum ;
     GraphKind kind;   //图的种类
 };
 class Graph
 {
 private:
     MGraph G;
 public:
     Graph();
     void CreateUDG();//创建无向图
     void CreateUDN();//创建无向网
     void CreateDG(); //创建有向图
     void CreateDN(); //创建有向网
     void CreateUDG_BYFile();//创建无向图,通过文件
     void CreateUDN_BYFile();//创建无向网,通过文件
     void CreateDG_BYFile(); //创建有向图,通过文件
     void CreateDN_BYFile(); //创建有向网,通过文件
     int LocateVex(VertexType u); //以顶点名称确定其邻接矩阵中的位置
     void  Display();//展示图或网的顶点向量，和邻接矩阵
 };

2.文件Graph_Matrix.cpp

 #include "stdafx.h"
 Graph::Graph()
 {
     cout<<"请输入图G的类型（ 有向图：0； 有向网：1； 无向图 ：2； 无向网 3；）"<<endl;
     scanf("%d",&G.kind);
     switch(G.kind)
     {
         case UDG: CreateUDG();
                   break;
         case UDN: CreateUDN();
                   break;
         case DG: CreateDG();
                   break;
         case DN: CreateDN();
                   break;
     }
 }
 void Graph::CreateUDG()
 {
     /*采用数组（邻接矩阵）表示法，构造无向图G
       以边为输入单位，即输入边的俩个顶点
       关键在于判断输入顶点是否存在，返回其位置
     */
     int i,j,IncInfo;//是否包含边或弧的相关信息
     VertexType  va,vb;
     cout<<"请输入无向图的顶点数，边数，变是否包含其他信息（是：1； 否；0；）"<<endl;
     cin>>G.vexnum;//顶点数
     cin>>G.arcnum;//边数
     cin>>IncInfo;//是否具有相关信息的判断条件
     cout<<"请输入"<<G.vexnum<<"个顶点的的值"<<endl;
     for(i=; i<G.vexnum; i++)//构造顶点向量
     {
         cin>>G.vex[i];
     }
     for(i=; i<G.vexnum; i++)//初始化邻接矩阵
     {
         for(j=; j<G.vexnum; j++)
         {
             G.arcs[i][j].adj=;//图
             G.arcs[i][j].info="NULL";//初始化为空串
         }
     }
     cout<<"请输入"<<G.arcnum<<"条边的顶点1，顶点2："<<endl;
     for(int k=; k<G.arcnum; k++)//按边录入信息
     {
         cin>>va;
         i=LocateVex(va);//查询下标,va所在的行坐标
         cin>>vb;
         j=LocateVex(vb);//查询下标,vb所在的行坐标
         G.arcs[i][j].adj=;  //表示va 与 vb 相连  无向图
         G.arcs[j][i].adj=;  //表示va与vb相连     无向图
         if(IncInfo)
         {
             cout<<"请输入该边相关信息"<<endl;
             cin>>G.arcs[i][j].info;  //输入字符串
             G.arcs[j][i].info=G.arcs[i][j].info;//对称阵
         }
     }
     G.kind=UDG;  //创建成功
 }
 void Graph::CreateUDN()
 {
     /*
         原理和UDG相同，只是增加了权值的输入
     */
     int i,j,IncInfo;//是否包含边或弧的相关信息
     VertexType  va,vb;
     cout<<"请输入无向网的顶点数，边数，变是否包含其他信息（是：1； 否；0；）"<<endl;
     cin>>G.vexnum;//顶点数
     cin>>G.arcnum;//边数
     cin>>IncInfo;//是否具有相关信息的判断条件
     cout<<"请输入"<<G.vexnum<<"个顶点的的值"<<endl;
     for(i=; i<G.vexnum; i++)//构造顶点向量
     {
         cin>>G.vex[i];
     }
     for(i=; i<G.vexnum; i++)//初始化邻接矩阵
     {
         for(j=; j<G.vexnum; j++)
         {
             G.arcs[i][j].adj=INFINITY;//网，无穷大表示不连接
             G.arcs[i][j].info="NULL";//初始化为空串
         }
     }
     for(int k=; k<G.arcnum; k++)//按边录入信息
     {
         cout<<"请输入第"<<k+<<"条边的顶点1，顶点2："<<endl;
         cin>>va;
         i=LocateVex(va);//查询下标,va所在的行坐标
         cin>>vb;
         j=LocateVex(vb);//查询下标,vb所在的行坐标
         cout<<"请输入权值"<<endl;
         cin>>G.arcs[i][j].adj;
         G.arcs[j][i].adj=G.arcs[i][j].adj;
         if(IncInfo)
         {
             cout<<"请输入该边相关信息"<<endl;
             cin>>G.arcs[i][j].info;  //输入字符串
             G.arcs[j][i].info=G.arcs[i][j].info;//对称阵
         }
     }
     G.kind=UDN;  //创建成功
 }
 void Graph::CreateDG()
 {
     /*
         原理与UDG相同，邻接矩阵略有区别
     */
     int i,j,IncInfo;//是否包含边或弧的相关信息
     VertexType  va,vb;
     cout<<"请输入有向图的顶点数，边数，变是否包含其他信息（是：1； 否；0；）"<<endl;
     cin>>G.vexnum;//顶点数
     cin>>G.arcnum;//边数
     cin>>IncInfo;//是否具有相关信息的判断条件
     cout<<"请输入"<<G.vexnum<<"个顶点的的值"<<endl;
     for(i=; i<G.vexnum; i++)//构造顶点向量
     {
         cin>>G.vex[i];
     }
     for(i=; i<G.vexnum; i++)//初始化邻接矩阵
     {
         for(j=; j<G.vexnum; j++)
         {
             G.arcs[i][j].adj=;//图
             G.arcs[i][j].info="NULL";//初始化为空串
         }
     }
     cout<<"请输入"<<G.arcnum<<"条弧的弧头，弧尾："<<endl;
     for(int k=; k<G.arcnum; k++)//按边录入信息
     {
         cin>>va;
         i=LocateVex(va);//查询下标,va所在的行坐标
         cin>>vb;
         j=LocateVex(vb);//查询下标,vb所在的行坐标
         G.arcs[j][i].adj=;  //表示vb(弧尾) 与 vb（弧头） 相连,也就是说vb可以到达va，反之不一定  有向图 vb——>va
         if(IncInfo)
         {
             cout<<"请输入该弧相关信息"<<endl;
             cin>>G.arcs[i][j].info;  //输入字符串
             G.arcs[j][i].info=G.arcs[i][j].info;//对称阵
         }
     }
     G.kind=DG; //创建成功
 }
 void Graph::CreateDN()
 {
     /*
         原理和DG相同，只是增加了权值的输入
     */
     int i,j,IncInfo;//是否包含边或弧的相关信息
     VertexType  va,vb;
     cout<<"请输入有向网的顶点数，边数，变是否包含其他信息（是：1； 否；0；）"<<endl;
     cin>>G.vexnum;//顶点数
     cin>>G.arcnum;//边数
     cin>>IncInfo;//是否具有相关信息的判断条件
     cout<<"请输入"<<G.vexnum<<"个顶点的的值"<<endl;
     for(i=; i<G.vexnum; i++)//构造顶点向量
     {
         cin>>G.vex[i];
     }
     for(i=; i<G.vexnum; i++)//初始化邻接矩阵
     {
         for(j=; j<G.vexnum; j++)
         {
             G.arcs[i][j].adj=INFINITY;//网，无穷大表示不连接
             G.arcs[i][j].info="NULL";//初始化为空串
         }
     }
     for(int k=; k<G.arcnum; k++)//按边录入信息
     {
         cout<<"请输入第"<<k+<<"条弧的弧头，弧尾："<<endl;
         cin>>va;
         i=LocateVex(va);//查询下标,va所在的行坐标
         cin>>vb;
         j=LocateVex(vb);//查询下标,vb所在的行坐标
         cout<<"请输入权值"<<endl;
         cin>>G.arcs[j][i].adj;
         if(IncInfo)
         {
             cout<<"请输入该弧相关信息"<<endl;
             cin>>G.arcs[i][j].info;  //输入字符串
             G.arcs[j][i].info=G.arcs[i][j].info;//对称阵
         }
     }
     G.kind=DN;  //创建成功
 }
 int  Graph::LocateVex(VertexType u)//给定顶点值，返回顶点在顶点数组中的下标，方便按边录入信息
 {
     for(int i=; i<G.vexnum; i++)
     {
         if(G.vex[i]==u)
         {
             return i;
         }
     }
     return -;
 }
 void Graph::Display()
 {
     cout<<"顶点向量"<<endl;
     for(int i=; i<G.vexnum; i++)
     {
         cout<<"顶点"<<G.vex[i]<<endl;
     }
     cout<<"邻接矩阵"<<endl;
     for(int i=; i<G.vexnum; i++)
     {
         for(int j=;j<G.vexnum;j++)
         {
             cout<<G.arcs[i][j].adj<<"\t";
         }
         cout<<endl;
     }
     cout<<"顶点1  顶点2    信息"<<endl;
     if(G.kind>) //对于无向图或者无向网来说，邻接矩阵是对称的
     {
         for(int i=; i<G.vexnum; i++)
         {
             for(int j=;j<i;j++)
             {
                 if(G.arcs[i][j].adj!=&&G.arcs[i][j].adj!=INFINITY)
                 {
                     cout<<G.vex[i]<<"\t";
                     cout<<G.vex[j]<<"\t";
                     cout<<G.arcs[i][j].info<<endl;
                 }
             }
         }
     }
     else//对于有向图或者有向网来说，邻接矩阵必须要全部输出
     {
         for(int i=; i<G.vexnum; i++)
         {
             for(int j=;j<G.vexnum;j++)
             {
                 if(G.arcs[i][j].adj!=&&G.arcs[i][j].adj!=INFINITY)
                 {
                     cout<<G.vex[i]<<"\t";
                     cout<<G.vex[j]<<"\t";
                     cout<<G.arcs[i][j].info<<endl;
                 }
             }
         }
     }
 }
 int _tmain(int argc, _TCHAR* argv[])
 {
     Graph g;
     g.Display();
     return ;
 }