2017.07.07【NOIP提高组】模拟赛B组

Summary

　　因为某种无法抗拒的原因，今天没有打比赛，所以也就没有那种心态。今天的题目有状压DP和二分，这套题不难也不简单，适中，适合我这种渣渣来做。在改题时，发现了许多问题。我连欧拉函数的计算都记错了，二分也忘记了。也总结出了一些经验，例如，在二分小数时，一定要比题目要求多加两位小数，这样也就避免了许多因为浮点数而造成的错误。长话短说，先看题。

Problem

T1 原根(math)

题目大意

　　给出两个定义，对于不超过m的正整数a，Gcd(m,a)=1，定义Ord_m(a)为a^d≡1(mod m)的最小正整数解。给出m，问有多少个a满足Ord_m(a)=φ(m)

想法

　　这是一道数学题，当然就要想一些数学的方法来优化了

　　根据欧拉公式，若Gcd(a,m)=1，那么a^φ(m)≡1(mod m)，显然春天不远了d是不会大于φ(m)的。

　　然后，我们就按照题目说的做，喜欢的人可以加上快速幂优化。

　　其中，φ(m)是读phi，是有计算公式的！可以百度一下，你就会知道了

T2 道路覆盖(cover)

题目大意　　

　　ar把一段凹凸不平的路分成了高度不同的N段，并用H[i]表示第i段高度。现在Tar一共有n种泥土可用，它们都能覆盖给定的连续的k个部分。对于第i种泥土，它的价格为C[i]，可以使得区间[i,min(n,i+k-1)] 的路段的高度增加E[i]。Tar要设定一种泥土使用计划，使得使用若干泥土后，这条路最低的高度尽量高，并且这个计划必须满足以下两点要求：

　　（1）每种泥土只能使用一次。
　　（2）泥土使用成本必须小于等于M。
　　请求出这个最低的高度最高是多少

想法

　　从“最低的高度最高”就可以看出，这道题是用二分的，正解就是二分答案。

　　从而，我们就把这道题目变为一道判定性的问题，给出一个mid，问你是否符合上面的题意。

　　普通方法使用递归判断可行性

　　既然可以用递归，那么显然可以用动态规划。

　　我们设F[i,s]表示你当前想选第i种泥土，前面k种的状态（包括i）是什么，用二进制表示,，0表示在那个位置没用了泥土，1表示用了。（用没用表示从他开始往后铺，专属于他的泥土）一定要看下面第二个图

　　我们用当前F[i,s]去更新F[i+1,s1]

　　关键是我们怎么转移。

　　对于每一种泥土，只有选和不选两种状态，那么我们只要考虑这两种情况就可以了

　　在此之前，我们先看一个东西

　　

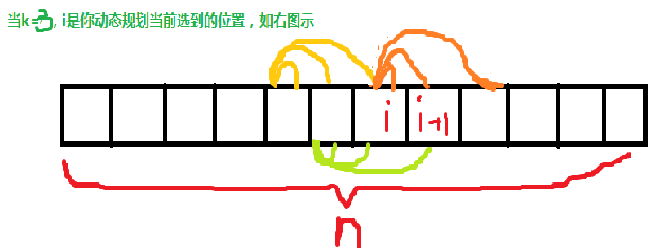
　　注意，我们这里是用i，更新i+1

　　读图可以发现，对i+1有影响的只有从i前k-1个（包括i）

　　可以发现，只有i包括i的前k-1个对i+1是有影响的。

　　因为你选到i时，状态是s，那么，如果从i更新到i+1，状态就是s去掉最后一位，也就是(s>>1)，其实就是s/2

　　我们统计s状态中，有哪个地方是选了泥土的，然后记录一下，他们一共会让i+1这个位置的土地高多少，设这个数为num，要多看图，多写草稿

　　为什么呢，因为前面的加了对应的e数组的某一个值，又因为它会影响到当前这个位置，看上图，所以，我们要看看，他们究竟影响到i+1这个位置增加多少值，所以我们要提前记录下来

　　其中S是枚举的！枚举的！枚举的！

　　

　　①不选

　　如果不选，那么num+h[i]必定是大于等于mid的，这样才符合题目要求，如果不懂反复读上面的那句话，看看我画出来精美的图，就知道了。不懂都会懂

　　满足的上面的情况，我们就可以转移了

　　f[i+1,s>>1]:=min(f[i+1,s>>1]，f[i,s])　

　　②选

　　如果选，就要满足num+h[i]+E[i]是大于等于mid的，同理也是上面所说

　　那么当前的位置s状态中i+1的位置应该是1，所以，我们就是要更新新的s

　　f[i+1,s>>1 or 1 shl (k-1)]:=min(f[i+1,s>>1 or 1 shl (k-1)]，f[i,j]+c[i]);

　　最后答案的判断就是判断有没有一个被更改过值得f[n,i](i是状态)是小于等于m的，因为在前面的操作中，都保证了更新过的f数组是符合题目要求的

　　这道题充分的体现了动态规划的屌

T3 迷宫花园(maze) 

题目大意

　　知道左右走花费1时间，上下走花费v时间，v是未知的，给出一个图（有障碍），再给出从起点到终点最少花费的时间，求v的值。

想法

　　显然也是用二分，二分v的值

　　然后用得出来的v去跑一次SPFA或者DIS，看看最短时间是否为题目给定的。

　　这里总结出一点：

　　　　要是对于小数二分，一定要多二分几位。

　　有的人只要跑一次bfs，我觉得很神奇，但是也弄不清原因。