算法导论 第六章 堆排序(python)
6.1堆
卫星数据:一个带排序的的数通常是有一个称为记录的数据集组成的,每一个记录有一个关键字key,记录的其他数据称为卫星数据。
原地排序:在排序输入数组时,只有常数个元素被存放到数组以外的空间中去。
在第二章介绍了两种排序:插入排序和合并排序,接下来两章要介绍的是推排序和快速排序,这四个排序都属于比较排序(comparison sort)。
快速排序的性能一般优先于堆排序
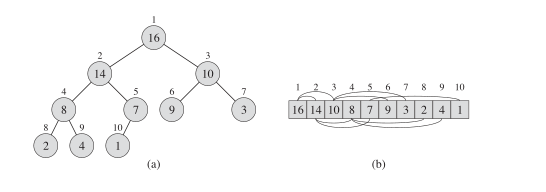
二叉堆是一个数组(b),近似完全二叉树(a)
数组(b) 实际的存储形势
二叉树(a) 要表达的结构
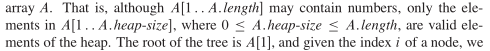
[1,A.heap-size] 闭区间的范围是堆(python一0开始 选择 [0,A.heap-size+1]的数组 怎么舍弃第一位? -1 ? 0 ? )

PARENT 返回的i的父亲结点在数组b中的下标 如i = 2 ->PARENT(2) ==1
LEFT 返回的i的左孩子结点在数组b中的下标 如i = 2 ->LEFT(2) ==4
RIGHT 返回的i的右孩子结点在数组b中的下标 如i = 2 ->LEFT(2) ==5
这3条是用数组(顺序表)表达堆(完全二叉树)的关键
特别注明i(数组下标)必须是从1开始{python中我舍弃第一位 data = [-1,] }
def PARENT(i):
return i//2 #为什么是一半 参考离散数学和数据结构
#我的解释是:二叉树的性质+下标从1开始
def LEFT(i):
return i*2 #同上
def RIGHT(i):
return i*2 + 1 #同上最大堆定义:所以父结点比孩子结点大
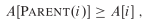 #堆排序使用 关键所在 调堆和建堆都是保证他
#堆排序使用 关键所在 调堆和建堆都是保证他
#堆排序就是将他的根节点{堆顶}取出来-->调堆-->将他的根节点{堆顶}取出来-->调堆-...直到堆只有一个数
最小堆定义:所以父结点比孩子结点小
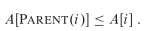
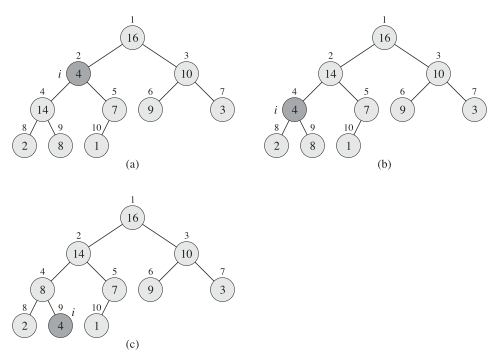
6.2维护堆的性质(调堆)
讲A[i] 和他的2个孩子对比最大的放在A[i]的位置
如果A[i]就是最大值的就结束
否则交换A[i] 和A[x] 再递归调节x结点
上图:

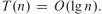
class Mylist(list):
def __init__(self):
self.heap_size = 0
super().__init__()
def MAX_HEAPIFY(A,i):
l = LEFT(i)
r = RIGHT(i)
#找出最大的结点
#i的左孩子是否大于i
#A.heap_size 写一个继承了list类 类中加上这个参数(Mylist)
#或者选择A[0] 位放heap_size ??
#或者设计全局变量
if l <= A.heap_size and A[l] > A[i]:
largest = l
else:
largest = i
#和右孩子比
if r <= A.heap_size and A[r] > A[largest]:
largest = r
if largest != i: #如果A[i]不是最大的 就要调堆了
A[i],A[largest] = A[largest],A[i] #交换
MAX_HEAPIFY(A,largest) #递归调largest6.3建堆
从最后一个有子树的(图中坐标5 = 10//2)的结点向根节点(图中坐标1)调堆
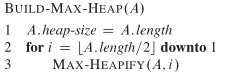
def BUILD_MAX_HEAP(A):
A.heap_size = len(A)-1
#print(len(A))
for i in range(A.heap_size//2,0,-1): #从n//2开始到1
#print(i)
MAX_HEAPIFY(A,i)
(在纸上画一遍就知道怎么回事了)
O(n)
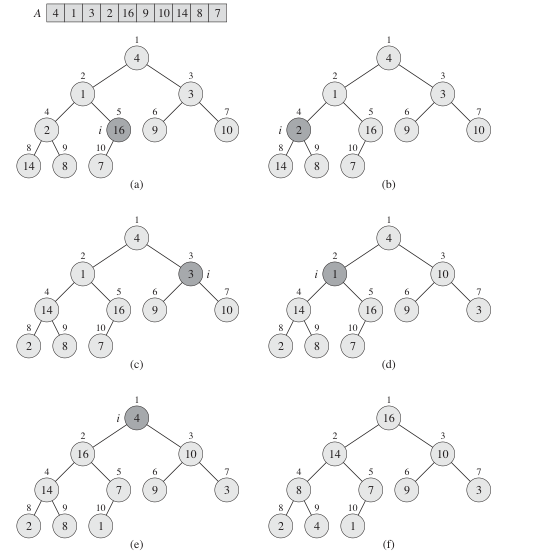
6.4堆排序算法
建立最大堆后(如a)显然16(A[1])是最大的,取出最大的,再调堆,再取出最大的。。。。。

def HEAPSORT(A):
BUILD_MAX_HEAP(A) #建堆
print("建成的堆:",A)
for i in range(len(A)-1,1,-1):
A[1],A[i] = A[i],A[1] #第一位和最后有位换
A.heap_size = A.heap_size - 1 #取出了一个
MAX_HEAPIFY(A,1) #调堆
if __name__ == '__main__':
A = Mylist()
#print(type(A))
for i in[-1,4,1,3,2,16,9,10,14,8,7]: #A = [,...] A会变成list
A.append(i)
#print(type(A))
HEAPSORT(A)
print("堆排序后:",A)
'''
============== RESTART: F:\python\algorithms\6_2_max_heapify.py ==============
建成的堆: [-1, 16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
堆排序后: [-1, 1, 2, 3, 4, 7, 8, 9, 10, 14, 16]
环境win7 + python3.5.1
'''
引用参考:
http://blog.csdn.net/littlethunder/article/details/23877545
http://www.wutianqi.com/?cat=515&paged=5
http://blog.csdn.net/hanchengxi/article/details/8454754
算法导论 第六章 堆排序(python)的更多相关文章
- 算法导论 第六章 2 优先队列(python)
优先队列: 物理结构: 顺序表(典型的是数组){python用到list} 逻辑结构:似完全二叉树 使用的特点是:动态的排序..排序的元素会增加,减少#和快速排序对比 快速一次排完 增 ...
- 算法导论 第六章 思考题6-3 Young氏矩阵
这题利用二叉堆维持堆性质的办法来维持Young氏矩阵的性质,题目提示中写得很清楚,不过确实容易转不过弯来. a,b两问很简单.直接看c小问: 按照Young氏矩阵的性质,最小值肯定在左上角取得,问题在 ...
- 算法导论 第六章 思考题 6-3 d叉堆
d叉堆的实现相对于二叉堆变化不大,首先看它如何用数组表示. 考虑一个索引从1开始的数组,一个结点i最多可以有d个子结点,编号从id - (d - 2) 到 id + 1. 从而可以知道一个结点i的父结 ...
- 《算法导论》第二章demo代码实现(Java版)
<算法导论>第二章demo代码实现(Java版) 前言 表示晚上心里有些不宁静,所以就写一篇博客,来缓缓.囧 拜读<算法导论>这样的神作,当然要做一些练习啦.除了练习题与思考题 ...
- 《算法》第六章部分程序 part 7
▶ 书中第六章部分程序,加上自己补充的代码,包括全局最小切分 Stoer-Wagner 算法,最小权值二分图匹配 ● 全局最小切分 Stoer-Wagner 算法 package package01; ...
- 《算法》第六章部分程序 part 6
▶ 书中第六章部分程序,包括在加上自己补充的代码,包括二分图最大匹配(最小顶点覆盖)的交替路径算法和 HopcroftKarp 算法 ● 二分图最大匹配(最小顶点覆盖)的交替路径算法 package ...
- 《算法》第六章部分程序 part 5
▶ 书中第六章部分程序,包括在加上自己补充的代码,网络最大流 Ford - Fulkerson 算法,以及用到的流量边类和剩余流量网络类 ● 网络最大流 Ford - Fulkerson 算法 pac ...
- 为什么我要放弃javaScript数据结构与算法(第六章)—— 集合
前面已经学习了数组(列表).栈.队列和链表等顺序数据结构.这一章,我们要学习集合,这是一种不允许值重复的顺序数据结构. 本章可以学习到,如何添加和移除值,如何搜索值是否存在,也可以学习如何进行并集.交 ...
- 《算法导论》— Chapter 6 堆排序
序 本文主要介绍堆排序算法(HeapSort),堆排序像合并排序而不像插入排序,堆排序的运行时间为O(nlgn):像插入排序而不像合并排序,它是一种原地(in place)排序算法.在任何时候,数组中 ...
随机推荐
- 《统计学习方法》笔记三 k近邻法
本系列笔记内容参考来源为李航<统计学习方法> k近邻是一种基本分类与回归方法,书中只讨论分类情况.输入为实例的特征向量,输出为实例的类别.k值的选择.距离度量及分类决策规则是k近邻法的三个 ...
- Codeforces Round #261 (Div. 2) C
Description Recently Pashmak has been employed in a transportation company. The company has kbuses a ...
- Substring CodeForces - 919D
http://codeforces.com/problemset/problem/919/D 就是先判环,如果有环就-1,否则对每个字母分开跑一下dp 错误记录: 1.有向图判环,自环一定要特判!(不 ...
- Jumping on Walls CodeForces - 198B
Jumping on Walls CodeForces - 198B 应该是一个隐式图的bfs,或者叫dp. 先是一个TLE的O(nklogn) #include<cstdio> #inc ...
- h5-18-文件操作-兼容判断
<!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title> ...
- Win10 Hyper-v 中安装 CentOS 搭建开发环境
Windows 环境 操作系统:Windows 10 开发环境:VS2005(需启动.NET Framework 3.5 ,才能正常安装使用) Linux 环境 发行版:CentOS 7_x64 安 ...
- TNS-12508 When Issuing Any SET Command For The Listene
TNS-12508 When Issuing Any SET Command For The Listener fact: Oracle Net Services fact: TNS Liste ...
- webkit滤镜
-webkit-filter: grayscale(1);/*灰度*/ -webkit-filter: sepia(1);/*褐色*/ -webkit-filter: saturate(1);/*饱和 ...
- 让搜狗输入法更符合编程/vim使用的配置
1. “菜单”—“设置属性”—“常用”—“初始状态”里的“中/英文”选项,选中“英文” 2. 设置属性里的“高级”里的“高级模式”,点“英文输入法设置”,“启动时启用英文输入法”选中 3. 按键-中英 ...
- 动手实现 React-redux(二):结合 context 和 store
既然要把 store 和 context 结合起来,我们就先构建 store.在 src/index.js 加入之前创建的 createStore 函数,并且构建一个 themeReducer 来生成 ...

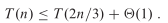 参考
参考