浅谈并查集 By cellur925【内含题目食物链、银河英雄传说等】

什么是并查集？

合并！查询！集合！

专业点说？

动态维护若干不重叠的和，支持合并查询的数据结构！（lyd老师说的）

数据结构特点：代表元。即为每个集合选择一个固定的元素，作为整个集合的代表，利用树形结构存储，每个节点都是一个元素，树根是集合的代表元素。（还是lyd老师说的）

两大基本操作

一、合并（merge()）

即把两个集合合并到一个的操作。通俗的说，即令其中一个树根为另一个树根的子节点。

void merge(int x,int y)
{
       fa[getf(x)]=getf(y);
}

二、查询（getf()）

朴素的查询效率太低，这里不再赘述。我们通常用到的高效方法是“路径压缩”（按秩合并由于在大多OI竞赛中并不必要，这里不再介绍）。

关于路径压缩，一图可以见真相。

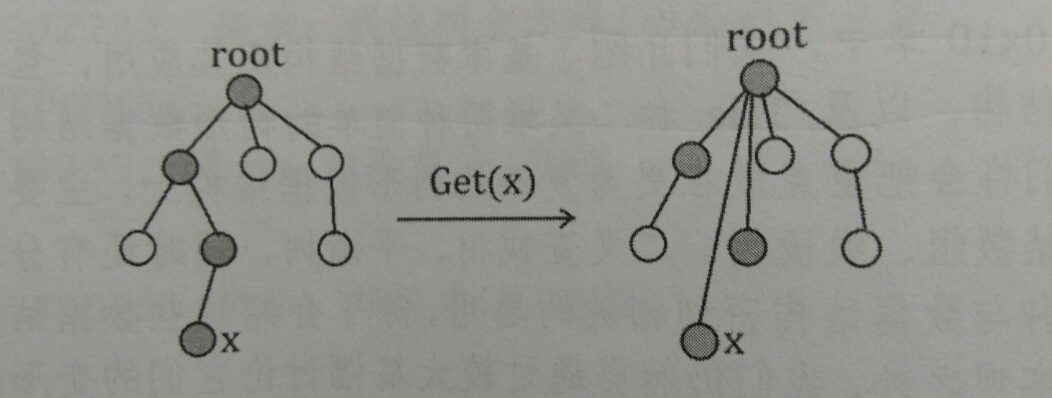
也就是每次在查询节点在集合内祖先时，不能直接调用f[x]，因为他是x的一个非根本祖先。而是调用getf函数通过迭代求解，在迭代的过程中，顺便完成了路径压缩。之后要提到的带权并查集、种类并查集与普通并查集的区别在getf上都有很大体系。可以说这一操作是并查集的核心。

这个操作的均摊复杂度为O（logN）。

int getf(int x)
{
       if(x==fa[x]) return x;
       return fa[x]=getf(fa[x]);
}

例题1 NOI2015程序自动分析

先要吐槽一句...这个题我自5月18号（大概）至今，已提交近30次，自己写的常数太丑，改了一次又一次，今天终于A了，所以...人活着还是要有梦想的嘛qwq。

是比较裸的并查集了，相等就进行合并操作，但注意本题数据离散程度较大，需要进行离散化。

献上我的卡线代码。

code

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 int t;
 int fa[];
 int n,cnt,a[],tot,b[];
 struct taojun{
     int p,q,op;
 }node[];
 void re(int &x)
 {
     x=;
     char ch=getchar();
     bool flag=false;
     while(ch<''||ch>'') flag|=(ch=='-'),ch=getchar();
     while(ch>=''&&ch<='') x=(x<<)+(x<<)+(ch^),ch=getchar();
     x=flag ? -x : x;
 }
 int getf(int x)
 {
     if(fa[x]==x) return x;
     else return fa[x]=getf(fa[x]);
 }
 void merge(int k,int h)
 {
     fa[getf(k)]=getf(h);
 }
 void discrete()
 {
     sort(a+,a+cnt+);
     tot=unique(a+,a+cnt+)-a-;
 }
 int query(int x)
 {
     return lower_bound(a+,a+tot+,x)-a;
 }
 void analyauto()
 {
     n=,cnt=,tot=;
     re(n);
     for(int i=;i<=n;i++)
     {
         int x=,y=,z=;
         re(x),re(y),re(z);
         node[i].p=x,node[i].q=y,node[i].op=z;
         a[++cnt]=x,a[++cnt]=y;
     }
     discrete();
     for(int i=;i<=n;i++)
     {
         node[i].p=query(node[i].p);
         node[i].q=query(node[i].q);
     }
     for(int i=;i<=tot;i++) fa[i]=i;
     for(int i=;i<=n;i++)
         if(node[i].op==) merge(node[i].p,node[i].q);
     for(int i=;i<=n;i++)
     {
         if(node[i].op==)
         {
             if(getf(node[i].p)==getf(node[i].q))
             {
                 printf("NO\n");
                 return;
             }
         }
     }
     printf("YES\n");
 }
 int main()
 {
     re(t);
     while(t--)
      analyauto();
     return ;
  } 

小结：并查集，在一张无向图中维护节点之间的连通性比较优秀，擅长动态维护许多有传递性的关系。

（还是lyd老师说的）

例题2 NOI2002银河英雄传说

LVYOUYW：神舟是哪年发射的来着？03？杨威利这个名字吼啊，莫非CCF提前一年已经知道了航天员杨利伟的名字？

2333...杨威利是真的存在的日本动漫《银河英雄传说》的主角...

学长您不会被打嘛...

扯淡结束

如果说并查集只是记录了集合的位置关系，那么在一些有权值的题目背景下，仅一个普通并查集维护关系貌似不太够用，我们还另需要一些数组来记录权值，本题就是这样。

我们可以维护一个数组d,用d[x]保存节点x到祖先节点fa[x]之间的边权。在路径压缩的同时，我们可以同时更新信息。

再用一个size[]在每个树根上记录集合大小，就能O（1）地进行查询。

code

 #include<cstdio>
 #include<algorithm>
 #include<cmath> 

 using namespace std;

 int T;
 int fa[],d[],size[];
 char ch;

 int getf(int p)
 {
     if(p==fa[p]) return p;
     int root=getf(fa[p]);
     d[p]+=d[fa[p]];
     return fa[p]=root;
 }

 void merge(int p,int q)
 {
     int pp=getf(p);
     int qq=getf(q);
     fa[pp]=qq;
     d[pp]=size[qq];
     size[qq]+=size[pp];
 }

 int main()
 {
     for(int i=;i<=;i++) fa[i]=i,size[i]=;
     scanf("%d",&T);
     ch=getchar();ch=getchar();
     while(T--)
     {
         int x=,y=;
         ch=getchar();
         if(ch=='M')
         {
             scanf("%d%d",&x,&y);
             merge(x,y);
         }
         if(ch=='C')
         {
             scanf("%d%d",&x,&y);
             if(getf(x)!=getf(y))
             {
                 printf("-1\n");
                 ch=getchar();ch=getchar();
                 continue;
             }
         //    printf("%d %d\n",d[x],d[y]);
         //    printf("%d\n",abs(d[x]-d[y]));
             printf("%d\n",abs(d[x]-d[y])-);
         }
         ch=getchar();ch=getchar();
     }
     return ;
 }

例题3 NOI2001 食物链

在我刚学并查集的时候，我用裸并查集骗了20分......

这种并查集，被lyd老师称为‘扩展域’，被学长称作“种类并查集”

当时他说这个偏移量的设计真是 妙 啊！

关于种类并查集，引用一位大神的话：“和基础并查集有很大一部分相同， 多了一个判断2个元素是否属于同一个集团（不是集合， 集合是用来判断2个元素是否能够判断他们属不属于同一个集团：有点绕， 举个例子， 假如知道1和2在不同的集团， 3和4在不同集团，我们就不能判断1和3是否属于一个集团，而集合是用来判断他们是否在同一个集团假如：已知1和2在不同集合，2和3在不同集合， 那么我们就知道1和3在同一个集合）；”  @Sky_sys，讲的很透彻

因为我在luogu看题解的时候，没有一个人跳出来解释原始的并查集作用是什么，看的我一脸mengbi。这下可是懂了。

于是，我们用一个数组flag[i]记录，表示i的祖先到i的偏移量，每次读入一句话，先看话中涉及的两动物是否在同一集合内，只有在同一集合内，才有可能继续判断；如果不在，我们先把它合并，假设当前这句话是对的。

合并的时候怎么搞？我们还是上一张图。

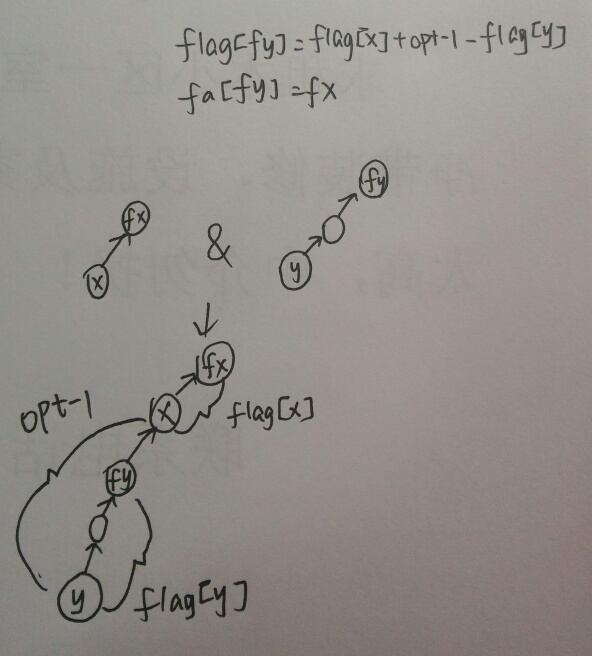
路径压缩的处理那里自己xjb推一下就好。记得取模！

code

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 int n,k,ans;
 int fa[],flag[];

 int getf(int x)
 {
     if(x==fa[x]) return x;
     int tmp=fa[x];
     fa[x]=getf(fa[x]);
     flag[x]=(flag[tmp]+flag[x])%;
     return fa[x];
 }

 int main()
 {
     scanf("%d%d",&n,&k);
     for(int i=;i<=n;i++) fa[i]=i;
     while(k--)
     {
         int ops=,a=,b=;
         scanf("%d%d%d",&ops,&a,&b);
         if(a>n||b>n)
         {
             ans++;
             continue;
         }
         if(ops==&&a==b)
         {
             ans++;
             continue;
         }
         int p=getf(a);
         int q=getf(b);
         if(p==q)
         {
             if((flag[b]-flag[a]+)%==ops-) continue;
             else ans++;
         }
         else//merge
         {
             flag[q]=(+ops-+flag[a]-flag[b])%;
             fa[q]=p;
         }
     }
     printf("%d",ans);
     return ;
 }

本文就要结束了，可是对于并查集，本蒟感觉还没有更深入理解qwq。所以过几天再刷几道题吧！qwq