Codeforces Round #106 (Div. 2) D. Coloring Brackets —— 区间DP

题目链接：https://vjudge.net/problem/CodeForces-149D

D. Coloring Brackets

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Once Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.

You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(") and closing (")") brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between the brackets. For example, such sequences as "(())()" and "()" are correct bracket sequences and such sequences as ")()" and "(()" are not.

In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the matching sixth one and the fifth bracket corresponds to the fourth one.

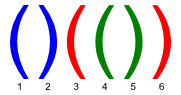
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:

• Each bracket is either not colored any color, or is colored red, or is colored blue.
• For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
• No two neighboring colored brackets have the same color.

Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo 1000000007 (109 + 7).

Input

The first line contains the single string s (2 ≤ |s| ≤ 700) which represents a correct bracket sequence.

Output

Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007(109 + 7).

Examples

input

(())

output

12

input

(()())

output

40

input

()

output

4

Note

Let's consider the first sample test. The bracket sequence from the sample can be colored, for example, as is shown on two figures below.

The two ways of coloring shown below are incorrect.

题解：

给出一串合法的括号，为括号上色，有如下原则：1）一对括号有且仅有一个是涂上颜色的， 2）颜色只有两种， 3）相邻的括号的颜色不允许相同（除非都没上色）。问：满足上述三个条件的上色方案有多少种？

1.由于给出的括号序列是合法的，即左括号与右括号一一对应。所以我们可以先预处理出每个左括号所对应的右括号。

2.详情请看代码注释。

写法一（人工枚举）：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = +;
 
 LL dp[MAXN][MAXN][][];
 int top, Stack[MAXN], match[MAXN];
 char s[MAXN];
 
 //区间为[l, r], isL为l-1处是否上色， isR为r+1处是否上色。
 LL dfs(int l, int r, bool isL, bool isR)
 {
     if(l>=r) return ;  //因为是乘法，所以遇到非法位置，就返回1。要是加法就return0或者1（实际情况实际考虑）。
     if(dp[l][r][isL][isR]!=-) return dp[l][r][isL][isR];
 
     LL ret = ;
     int k = match[l];  //找到与最左端的左括号匹配的右括号
 
     if(!isL)    //首先考虑为左括号上色。如果l-1处没有上色， 那么左括号就可以上两种颜色
         ret = (ret + (2LL*dfs(l+, k-, true, false)*dfs(k+, r, false, isR))%MOD)%MOD;
     else        //否则， 左括号只能上一种颜色，与l-1处括号相对的颜色
         ret = (ret + (1LL*dfs(l+, k-, true, false)*dfs(k+, r, false, isR))%MOD)%MOD;
     if(k!=r || (k==r&&!isR) )   //其次为右括号上色。如果右括号不在右端点，或者在右端点但是r+1处没有上色，则可上两种颜色
         ret = (ret + (2LL*dfs(l+, k-, false, true)*dfs(k+, r, true,  isR))%MOD)%MOD;
     else                     //否则，右括号在最右端且r+1处上了颜色，那么右括号只能上一种颜色。
         ret = (ret + (1LL*dfs(l+, k-, false, true)*dfs(k+, r, true,  isR))%MOD)%MOD;
 
     return dp[l][r][isL][isR] = ret;
 }
 
 int main()
 {
     while(scanf("%s", s+)!=EOF)
     {
         int n = strlen(s+);
         top = ;
         for(int i = ; i<=n; i++)  //为左括号找到匹配的右括号
         {
             if(s[i]=='(') Stack[top++] = i;
             else match[Stack[--top]] = i;
         }
 
         memset(dp, -, sizeof(dp));
         dfs(, n, , );
         printf("%lld\n", dp[][n][][]);
     }
 }

写法二（for枚举，推荐）：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = +;
 
 LL dp[MAXN][MAXN][][];
 int top, Stack[MAXN], match[MAXN];
 char s[MAXN];
 
 //区间为[l, r]，Lcol为l-1处的颜色， Rcol为r+1处的颜色，0代表没上色，1和2分别代表两种不同的颜色
 LL dfs(int l, int r, int Lcol, int Rcol)
 {
     if(l>=r) return ;  //因为是乘法，所以遇到非法位置，就返回1。要是加法就return0或者1（实际情况实际考虑）。
     if(dp[l][r][Lcol][Rcol]!=-) return dp[l][r][Lcol][Rcol];
 
     LL ret = ;
     int k = match[l];   //找到与最左端的左括号匹配的右括号
     for(int lc = ; lc<; lc++)     //枚举这个括号的着色情况，并且需要去除掉非法的情况
     for(int rc = ; rc<; rc++)
     {
         if((lc&&rc)||(!lc&&!rc)) continue;  //如果两个括号都没涂色或者都涂上颜色，非法
         if(lc && lc==Lcol) continue;      //如果l-1处涂上了颜色，且l处也要涂上相同的颜色， 非法
         if(k==r && rc && rc==Rcol) continue;    //如果匹配的右括号在最右端，且r+1处涂上了颜色，又尝试为
                                                 //右括号涂上相同的颜色，非法。如果右括号不在最右端，那么就无需
                                                 //考虑r+1处的着色情况了，因为右括号右边的括号必定没有上色。
         ret = (ret+(1LL*dfs(l+, k-, lc, rc)*dfs(k+, r, rc, Rcol))%MOD)%MOD;  //统计合法的情况
     }
     return dp[l][r][Lcol][Rcol] = ret;
 }
 
 int main()
 {
     while(scanf("%s", s+)!=EOF)
     {
         int n = strlen(s+);
         top = ;
         for(int i = ; i<=n; i++)   //为左括号找到匹配的右括号
         {
             if(s[i]=='(') Stack[top++] = i;
             else match[Stack[--top]] = i;
         }
 
         memset(dp, -, sizeof(dp));
         printf("%lld\n", dfs(, n, , ));
     }
 }