洛谷 P3381 【模板】最小费用最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

第一行包含四个正整数\(N、M、S、T\)，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来\(M\)行每行包含四个正整数\(u_i、v_i、w_i、f_i\)，表示第i条有向边从\(u_i\)出发，到达\(v_i\)，边权为\(w_i\)（即该边最大流量为\(w_i\)），单位流量的费用为\(f_i\)。

输出格式：

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

输入输出样例

输入样例#1：

4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5

输出样例#1：

50 280

说明

时空限制：\(1000ms,128M\)

（BYX：最后两个点改成了\(1200ms\)）

数据规模：

对于\(30\%\)的数据：\(N<=10，M<=10\)

对于\(70\%\)的数据：\(N<=1000，M<=1000\)

对于\(100\%\)的数据：\(N<=5000，M<=50000\)

样例说明：

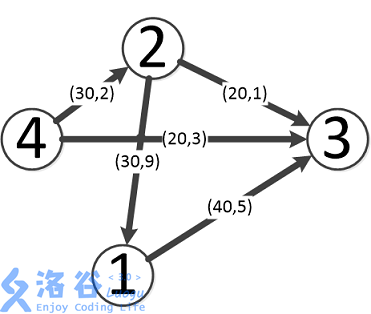
如图，最优方案如下：

第一条流为\(4-->3\)，流量为\(20\)，费用为\(3*20=60\)。

第二条流为\(4-->2-->3\)，流量为\(20\)，费用为\(（2+1）*20=60\)。

第三条流为\(4-->2-->1-->3\)，流量为\(10\)，费用为\(（2+9+5）*10=160\)。

故最大流量为\(50\)，在此状况下最小费用为\(60+60+160=280\)。

故输出\(50\) \(280\)。

思路：费用流的模板题，就是在最大流中用，\(spfa\)或\(dijkstra\)等算法来代替，不同的是费用流在管流量的同时也要管边权，所以，可以说算是最大流的升级版吧，我目前还只会\(spfa\)版本的，\(dijkstra\)的还不太会写。

代码：

#include<cstdio>
#include<cstring>
#include<cctype>
#include<queue>
#define maxn 5007
using namespace std;
int num=1,n,m,head[maxn],pre[maxn],dis[maxn],vis[maxn],maxflow,ans,S,T;
const int inf=0x3f3f3f3f;
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct node {
  int u,v,f,w,nxt;
}e[maxn*20];
inline void ct(int u, int v, int f, int w) {
  e[++num]=node{u,v,f,w,head[u]};
  head[u]=num;
}
inline bool bfs() {
  memset(vis,0,sizeof(vis));
  memset(dis,0x3f,sizeof(dis));
  queue<int>q;
  q.push(S),dis[S]=0;
  while(!q.empty()) {
    int u=q.front();
    q.pop();
    vis[u]=0;
    for(int i=head[u];i;i=e[i].nxt) {
      int v=e[i].v,f=e[i].f;
      if(dis[v]>dis[u]+e[i].w&&f) {
        dis[v]=dis[u]+e[i].w;
        pre[v]=i;
        if(!vis[v]) {
          vis[v]=1;
          q.push(v);
        }
      }
    }
  }
  return dis[T]!=inf;
}
inline void work() {
  int minn=inf;
  for(int i=T;i!=S;i=e[pre[i]].u)
    minn=min(minn,e[pre[i]].f);
  for(int i=T;i!=S;i=e[pre[i]].u) {
    e[pre[i]].f-=minn;
    e[pre[i]^1].f+=minn;
    ans+=minn*e[pre[i]].w;
  }
  maxflow+=minn;
}
int main() {
  n=qread(),m=qread(),S=qread(),T=qread();
  for(int i=1;i<=m;++i) {
    int u=qread(),v=qread(),f=qread(),w=qread();
    ct(u,v,f,w),ct(v,u,0,-w);
  }
  while(bfs()) work();
  printf("%d %d\n",maxflow,ans);
  return 0;
}