利用子集构造法实现NFA到DFA的转换

• 概述

NFA非有穷自动机，即当前状态识别某个转换条件后到达的后继状态不唯一，这种自动机不便机械实现，而DFA是确定有限状态的自动机，它的状态转换的条件是确定的，且状态数目往往少于NFA，所以DFA能够比较方便的机械实现且识别能力方面也和NFA相当。本次实验采用子集构造法来实现不带空弧的由NFA到DFA的转换。

子集构造法的算法如下：

设NFA为M=(K,Σ,f,S0,Z)，则构造相应的DFA  M′=(Q,Σ,f′,I0,F)
①取I0=S0；
②对于状态集Q中任一尚未标记的状态qi={Si1,Si2,…,Sim},Sik∈K，做：
 (1) 标记qi；
 (2) 对于每个a∈Σ，置
     T=f({Si1,Si2,…,Sim},a)
     qj=εCLOSURE(T)
 (3) 若qj不在Q中，则将qj作为一个未加标记的状态添加到Q中，且把状态转移f′(qi,a)=qj添加到M′。
③重复进行步骤②，直到Q中不再含有未标记的状态为止。对于由此构造的Q，我们把那些至少含有一个Z中的元素的qi作为M′的终态。

对于如图所示的NFA其在文件中保存的信息如下

转成DFA之后的形式为

重命名为

• 程序整体思路

首先将文件中所给的NFA输入读入程序，在读入过程中将其以图的邻接表的形式保存，其中将状态转移条件记为该边的权值，每种状态记为图的结点，该状态识别状态转移条件(权值)之后到达的状态为该结点的邻接点。

对于上面的例子，将其读入程序中后该图在程序中的逻辑存储结构（图的邻接表）如图所示，其中邻接点中第一个数字表示权值，第二个数字表示所连的结点。

将图读入程序中后，再使用子集构造算法来完成由NFA到DFA的转化。

对于每种状态，其数据结构定义为

 typedef struct state
 {
     set<int> Set;
     char name;
 }state;

其中set里存放该状态识别某个条件后所能到达的状态集合的下标，name里存该状态重命名后的名字。

这些状态保存在状态数组States[max]中，状态数组States[max]数据结构定义为

 state States[max];

子集构造法的过程就是不断向状态数组States[ ]中，添加识别某个条件后，新的未出现的状态的过程。

程序中函数说明

void creatph(algraph &g,FILE *fpr)：将文件内容读入程序，并将其转换为图的邻接表子函数。

int change(algraph g,char p)：将图中结点转化为对应下标子函数。

state move(state s,int n,algraph g)：求当前状态集合的转移集合，即求s状态识别字母n之后的状态集合。

int equalSet(state m,state n)：比较两个状态的set集合内容是否相等，不相等返回0，相等返回1。

void inStates(state &s)：判断当前状态是否在States数组中存在，若存在，进行改名；若不存在，改名后加入States数组。

void changeToD(algraph g,FILE *fpw)：由NFA转到DFA的主控程序子函数。

程序输入如下图所示

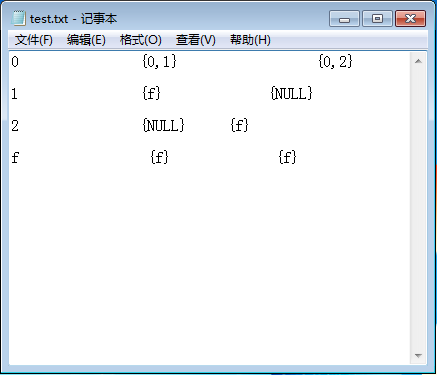
程序输出如下图所示

• 代码清单

 #include<stdio.h>
 #include<malloc.h>
 #include <iostream>
 #include <fstream>
 #include <cstring>
 #include<set>

 using namespace std;

 #define max 50//定义结点最大数量
 typedef char vertype;//定义结点值域为字符类型
 char buf[];//定义读文件内容时，程序缓冲数组
 int num;//记录有穷字母表元素的个数
 int length;//记录States数组的长度

 typedef struct arcnode//图的边信息
 {
     int adjvex;
     int weight;//边所对应的权值
     struct arcnode *next;
 }arcnode;

 typedef struct vnode//图的结点类型定义
 {
     vertype data;
     arcnode *next;
 }vnode,adjlist[max];

 typedef struct//图的定义
 {
     adjlist a;
     int vexnum,arcnum;
 }algraph;

 typedef struct state//状态的定义
 {
     set<int> Set;
     char name;
 }state;

 state States[max];

 int change(algraph g,char p)//将图中结点转化为对应下标
 {
     int i;
     for(i=;i<g.vexnum;i++)
     {
         if(p==g.a[i].data)
             return i;
     }
     return -;
 }

 void creatph(algraph &g,FILE *fpr)
 {
     int line = ;
     while(!feof(fpr))
     {
         fgets(buf,,fpr);
         if(strlen(buf)>)//获取文件中图的结点个数
         {
             int i = ;
             while(buf[i]==' ')
             {
                 i++;
             }

             g.a[line].data=buf[i];
             g.a[line].next=NULL;
             line++;
         }
     }
     g.vexnum=line;

     rewind(fpr);//将文件指针返回到开头位置
     line = ;
         arcnode *s;

     while(!feof(fpr))//再次扫描文件将边的信息添上，构造图
     {
         int weight=;//边所对应的权值,每一行权值都从0开始
         fgets(buf,,fpr);
         if(strlen(buf)>)
         {
             for(int i=;i<strlen(buf)-;i++)
             {
                 if(buf[i]=='{')
                 {
                     weight++;
                     if(num<weight)
                         num=weight;

                     i++;
                     if(buf[i]=='N')
                             i=i+;

                     while(buf[i]!='}')
                     {
                         if(buf[i]!=',')
                         {
                             //cout<<buf[i];////////////////////////////////
                             int x = change(g,buf[i]);

                             s=(arcnode *)malloc(sizeof(arcnode));
                             s->adjvex=x;
                             s->weight=weight;
                             s->next=g.a[line].next;
                             g.a[line].next=s;
                             //cout<<line;////////////////////////////////
                         }
                         i++;
                     }
                 }
             }
             line++;
         }
     }

 }

 state move(state s,int n,algraph g)//求当前状态集合的转移集合，即求s状态识别字母n之后的状态集合
 {
     state temp;
     arcnode *m;
     set<int>::iterator itr;//迭代器
     for(itr = s.Set.begin();itr!=s.Set.end();itr++)//遍历当前s状态中集合元素
     {
         int i = *itr;
         m = g.a[i].next;
         while(m)
         {
             if(m->weight==n)
             {
                 temp.Set.insert(m->adjvex);//cout<<m->adjvex<<" ";
             //    temp.name=s.name+1;//cout<<temp.name<<endl;
             }
             m=m->next;
         }
     }
     return temp;
 }

 int equalSet(state m,state n)//比较两个状态的set集合内容是否相等
 {
     int flag = ;
     if(m.Set.size()!=n.Set.size())
     {
         flag = ;
         return flag;
     }

     set<int>::iterator itrm;
     set<int>::iterator itrn;
     for(itrm = m.Set.begin(),itrn = n.Set.begin();itrm!=m.Set.end();itrm++,itrn++)
     {
         int m = *itrm;
         int n = *itrn;

         if(m!=n)
         {
             flag = ;
             break;
         }
     }
     return flag;
 }

 void inStates(state &s)//判断当前状态是否在States数组中存在，若存在，进行改名；若不存在，改名后加入States数组
 {
     int flag = ;
     if(length==)
     {
         States[]=s;
         States[].name='A';
         length++;
     }
     else
     {
         for(int i=;i<length;i++)
         {
             //cout<<equalSet(States[i],s);
             if(equalSet(States[i],s)==)//若存在，进行改名
             {
                 s.name=States[i].name;
                 flag = ;
                 break;
             }
         }

         if(flag == )//若不存在，改名后加入States数组
         {
             s.name=States[length-].name+;
             States[length]=s;
             length++;
         }
     }
 }

 void changeToD(algraph g,FILE *fpw)
 {
     state s,temp;
     s.Set.insert();
     s.name='A';

     inStates(s);

     for(int i=;i<length;i++)
     {
         cout<<"{";
         fprintf(fpw,"{");

         set<int>::iterator itr;//迭代器
         for(itr = States[i].Set.begin();itr!=States[i].Set.end();itr++)//遍历当前s状态中集合元素
         {
             int i = *itr;
             cout<<g.a[i].data<<",";
             fprintf(fpw,"%c,",g.a[i].data);
         }

         cout<<"}";
         fprintf(fpw,"}");

         cout<<States[i].name;
         fprintf(fpw,"%c",States[i].name);

         for(int j=;j<=num;j++)
         {
             temp = move(States[i],j,g);
             inStates(temp);
             //查看temp状态的set集合
             /*
             set<int>::iterator itr;//迭代器
             for(itr = temp.Set.begin();itr!=temp.Set.end();itr++)//遍历当前s状态中集合元素
             {
                 int i = *itr;
                 cout<<i<<" ";
             }*/
             cout<<temp.name;
             fprintf(fpw,"%c",temp.name);
         }
         cout<<endl;
         fprintf(fpw,"\n");
     }
 }

 int main()
 {
     algraph g;

     FILE *fpr = fopen("F:\\test.txt","r");
     FILE *fpw = fopen("F:\\testOutput.txt","w");

 /*    FILE *fpr = fopen("test.txt","r");
     FILE *fpw = fopen("output.txt","w");*/

     creatph(g,fpr);

     //create测试
     /*
     for(int i=0;i<g.vexnum;i++)
     {
         cout<<g.a[i].data<<endl;//////////////////

     }
     */

     changeToD(g,fpw);
     //move测试
     /*
     state s;
     s.Set.insert(0);
     s.Set.insert(2);
     s.Set.insert(3);
     s.mark=1;
     s.name='B';

     move(s,2,g);
     */
     return ;
 }