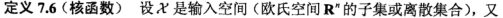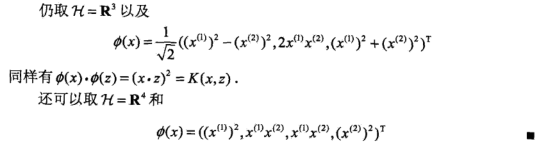统计学习方法:核函数(Kernel function)
作者:桂。
时间:2017-04-26 12:17:42
链接:http://www.cnblogs.com/xingshansi/p/6767980.html

前言
之前分析的感知机、主成分分析(Principle component analysis, PCA)包括后面看的支撑向量机(Support vector machines, SVM),都有用到核函数。核函数是将信号映射到高维,而PCA一般用来降维。这里简单梳理一下核函数的知识:
1)核函数基本概念;
2)核函数的意义;
内容为自己的学习记录,其中多有参考他人,最后一并给出链接。
一、核函数基本概念
先来看看核函数的定义:
核函数:是映射关系 的内积,映射函数本身仅仅是一种映射关系,并没有增加维度的特性,不过可以利用核函数的特性,构造可以增加维度的核函数,这通常是我们希望的。
的内积,映射函数本身仅仅是一种映射关系,并没有增加维度的特性,不过可以利用核函数的特性,构造可以增加维度的核函数,这通常是我们希望的。
例如这样一个图:
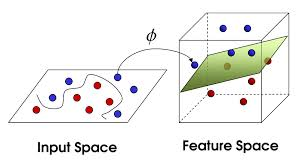
二维映射到三维,区分就更容易了,这是聚类、分类常用核函数的原因。为什么PCA这样一个降维算法也用核函数呢?
左图为原数据,右图为映射到三维的数据,可以看出:同样是降到1维,先通过Kernel映射到(Kernel是映射的内积,不要弄乱了)三维,再投影到1维,就容易分离开,这就是Kernel在PCA降维中的应用,本质还是对原有数据增加维度。
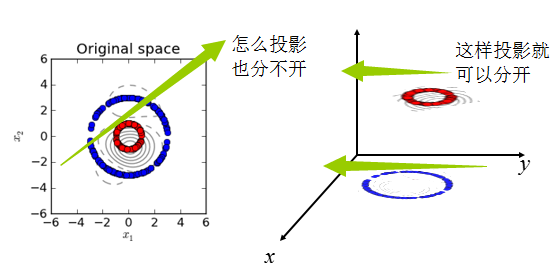
既然核函数这么神奇,就看看它的来龙去脉。
二、核函数的意义
A-核函数常见应用
先来看看核函数几个常用的地方:
1.核感知机
在前面分析感知机时提到:
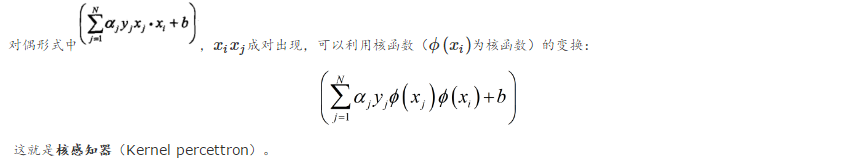
2.核聚类(Kernel Kmeans)
在前面分析核聚类时提到:

3.核PCA(kernel PCA)
具体定义可以参考wikipedia,根据前文分析的PCA步骤,有一步是利用相关矩阵的特征值分解,看看相关矩阵:
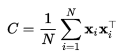
又看到了相乘的形式,自然可以用Kernel:
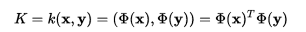
4.支撑向量机SVM
支撑向量机对偶形式的目标函数:
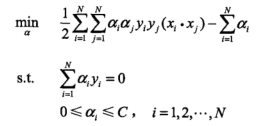
又看到了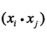 的形式,从而得到SVM的核函数形式:
的形式,从而得到SVM的核函数形式:
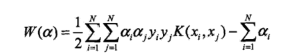
B-核函数为什么可以映射到高维?
1.为什么不用映射函数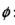 ,而用他们的内积形式,即Kernel函数?
,而用他们的内积形式,即Kernel函数?
因为(x,z)一起出现的时候,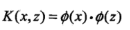 有许多固定的形式可以调用,而不必求解或者关心
有许多固定的形式可以调用,而不必求解或者关心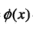 的具体形式,这大大简化了求解。
的具体形式,这大大简化了求解。
2.什么样的函数才可以叫做核函数?
直接给出条件:
具体参考:李航《统计学习方法》p120~122。
3.为什么实现数据映射到高维?
看一个例子:
这就从二维变成了三维,当然还可以更高维:
这里可以粗略理解成:多项式可以实现数据的维度扩增,而高斯核是指数形式,展开就是无穷多的多项式,所以高斯核可以将数据映射到无穷维度。
4.常用核函数
多项式核:

高斯核:

参考:
- 李航《统计学习方法》
统计学习方法:核函数(Kernel function)的更多相关文章
- 核函数(kernel function)
百度百科的解释: 常用核函数: 1.线性核(Linear Kernel): 2.多项式核(Polynomial Kernel): 3.径向基核函数(Radial Basis Function),也叫高 ...
- [转]核函数K(kernel function)
1 核函数K(kernel function)定义 核函数K(kernel function)就是指K(x, y) = <f(x), f(y)>,其中x和y是n维的输入值,f(·) 是从n ...
- 统计学习方法c++实现之六 支持向量机(SVM)及SMO算法
前言 支持向量机(SVM)是一种很重要的机器学习分类算法,本身是一种线性分类算法,但是由于加入了核技巧,使得SVM也可以进行非线性数据的分类:SVM本来是一种二分类分类器,但是可以扩展到多分类,本篇不 ...
- 统计学习方法:KNN
作者:桂. 时间:2017-04-19 21:20:09 链接:http://www.cnblogs.com/xingshansi/p/6736385.html 声明:欢迎被转载,不过记得注明出处哦 ...
- 李航《统计学习方法》CH01
CH01 统计学方法概论 前言 章节目录 统计学习 监督学习 基本概念 问题的形式化 统计学习三要素 模型 策略 算法 模型评估与模型选择 训练误差与测试误差 过拟合与模型选择 正则化与交叉验证 正则 ...
- 统计学习方法:支撑向量机(SVM)
作者:桂. 时间:2017-05-13 21:52:14 链接:http://www.cnblogs.com/xingshansi/p/6850684.html 前言 主要记录SVM的相关知识,参考 ...
- 统计学习方法—SVM推导
目录 SVM 1. 定义 1.1 函数间隔和几何间隔 1.2 间隔最大化 2. 线性可分SVM 2.1 对偶问题 2.2 序列最小最优算法(SMO) 3. 线性不可分SVM 3.1 松弛变量 3.2 ...
- 【NLP】基于统计学习方法角度谈谈CRF(四)
基于统计学习方法角度谈谈CRF 作者:白宁超 2016年8月2日13:59:46 [摘要]:条件随机场用于序列标注,数据分割等自然语言处理中,表现出很好的效果.在中文分词.中文人名识别和歧义消解等任务 ...
- 统计学习方法 --- 感知机模型原理及c++实现
参考博客 Liam Q博客 和李航的<统计学习方法> 感知机学习旨在求出将训练数据集进行线性划分的分类超平面,为此,导入了基于误分类的损失函数,然后利用梯度下降法对损失函数进行极小化,从而 ...
随机推荐
- KoaHub平台基于Node.js开发的Koa的rewrite and index support插件代码详情
koa-static-server Static file serving middleware for koa with directory, rewrite and index support k ...
- 大数据系列之Flume+HDFS
本文将介绍Flume(Spooling Directory Source) + HDFS,关于Flume 中几种Source详见文章 http://www.cnblogs.com/cnmenglang ...
- 九度OJ题目1208:10进制 VS 2进制 (JAVA)
题目描述: 对于一个十进制数A,将A转换为二进制数,然后按位逆序排列,再转换为十进制数B,我们乘B为A的二进制逆序数. 例如对于十进制数173,它的二进制形式为10101101,逆序排列得到1 ...
- SQLServer 数据库不能重命名的解决方案
无法用排他锁锁定该数据库,以执行该操作 SQL Server2008 因为可能其他用户在占用着该数据库 解决办法为 把数据库先改为单用户的,再改数据库名,再改回多用户的 USE [master] GO ...
- impress.js初体验
概述 如果你已经厌烦了使用PowerPoint制作PPT,那么impress.js是一个非常好的选择,用它做的PPT更加直观,效果也非常的不错.装X是需要一定代价的,不过如果你是个前端爱好者那么一切就 ...
- 实验楼-3-Linux用户及用户组
获得自己用户名 $ who am i $ whoami pts/0 : 伪终端/序号 root操作:sudo Firstly,知道当前登录用户的密码:Secondly,当前用户在sudo用户组 添加新 ...
- 解决Appium无元素可选的如何定位
1.首先我们看看要定位的东西,我要定位的就是折让率上图自己看 写代码: AndroidElement element = driver.findElementByAndroidUIAutomato ...
- JDBC(与Oracle的连接)(转)
JDBC编程步骤:----java与Oracle数据的连接(lomboz_eclipse环境下) 1.在Oracle数据库安装文件夹中找到jdbc文件夹→lib文件夹→classesl2.jar ...
- Oracle DQL查询语言整理
select * from t_hq_ryxx; select nianl, xingm from t_hq_ryxx; select nianl as 年龄, xingm as 姓名 from t_ ...
- API测试自动化——基于CDIF的SOA基本功能(实例篇)
今天我们通过一些实例来体验一下API的自动化测试,感受一下基于CDIF的SOA的一些基本功能. 传统的测试工具在测试一个API的时候,必须手动填写这个API所需要接收的所有信息,比如一个查询航班动态的 ...