平衡二叉树（AVL树）

参考资料

http://www.cnblogs.com/Cmpl/archive/2011/06/05/2073217.html

http://www.cnblogs.com/yc_sunniwell/archive/2010/06/27/1766236.html

http://www.cnblogs.com/suimeng/p/4560056.html

http://blog.csdn.net/gabriel1026/article/details/6311339

http://www.cnblogs.com/zhangbaochong/p/5164994.html

一、基本概念

平衡二叉查找树：

简称平衡二叉树。由前苏联的数学家Adelse-Velskil和Landis在1962年提出的高度平衡的二叉树，根据科学家的英文名也称为AVL树。它具有如下几个性质：

1. 可以是空树。
2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过1

平衡二叉树一定是二叉查找树。

平衡因子：

左子树的高度减去右子树的高度。由平衡二叉树的定义可知，平衡因子的取值只可能为0,1,-1.分别对应着左右子树等高，左子树比较高，右子树比较高。

最小失衡子树：在新插入的结点向上查找，以第一个平衡因子的绝对值超过1的结点为根的子树称为最小不平衡子树。也就是说，一棵失衡的树，是有可能有多棵子树同时失衡的，如下。而这个时候，我们只要调整最小的不平衡子树，就能够将不平衡的树调整为平衡的树。

二、算法

平衡二叉树算法思想

若 向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。首先要找出插入新结点后失去平衡的最小子树根结点的指针。然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。失去平衡的最小子树是指以离插入结点最近，且平衡因子绝对值大于1的结点作为根的子树。假设用A表示失去平衡的最小子树的根结点，则调整该子树的操作可归纳为下列四种情况。

1. LL型

个人理解

左旋：旋转中心的父节点绕旋转中心向左下旋转

右旋：旋转中心的父节点绕旋转中心向右下旋转

平衡二叉树某一节点的左孩子的左子树上插入一个新的节点，使得该节点不再平衡。这时只需要把树向右旋转一次即可，如图所示，原A的左孩子B变为父结点，A变为其右孩子，而原B的右子树变为A的左子树，注意旋转之后Brh是A的左子树（图上忘在A于Brh之间标实线）

 

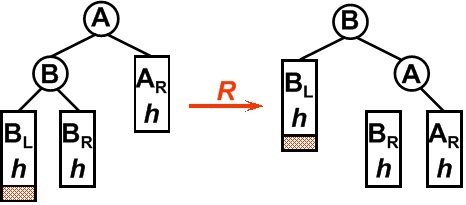
2. RR型

平衡二叉树某一节点的右孩子的右子树上插入一个新的节点，使得该节点不再平衡。这时只需要把树向左旋转一次即可，如图所示，原A右孩子B变为父结点，A变为其左孩子，而原B的左子树Blh将变为A的右子树。

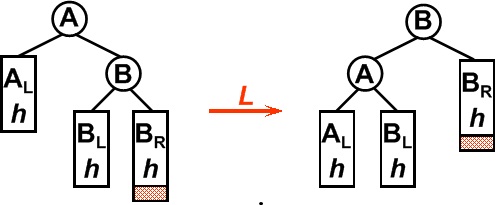
3. LR型（最小失衡子树的根节点（A）的左孩子(B)的右孩子（C）为旋转点左旋，然后再以这个点(C)右旋）

平衡二叉树某一节点的左孩子的右子树上插入一个新的节点，使得该节点不再平衡。这时需要旋转两次，仅一次的旋转是不能够使二叉树再次平衡。如图所示，在B节点按照RR型向左旋转一次之后，二叉树在A节点仍然不能保持平衡，这时还需要再向右旋转一次。

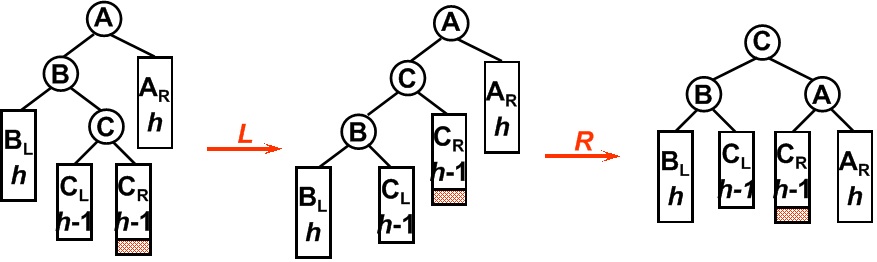
4. RL型（最小失衡子树的根节点（A）的右孩子(B)的左孩子（C）为旋转点右旋，然后再以这个点(C)左旋）

平衡二叉树某一节点的右孩子的左子树上插入一个新的节点，使得该节点不再平衡。同样，这时需要旋转两次，旋转方向刚好同LR型相反。

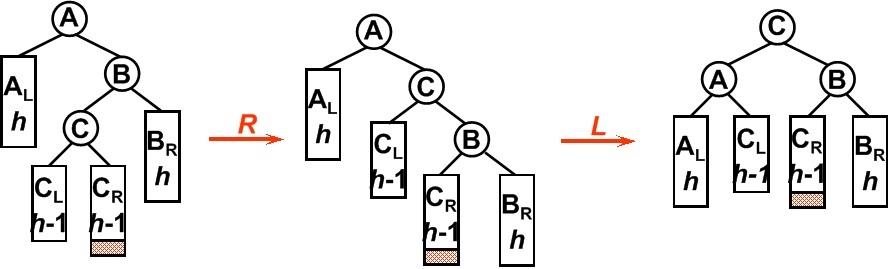
删除节点

删除则稍微麻烦点，因为我们删的不一定是叶子，如果只是叶子，那就好办，如果不是呢？我们最通常的做法就是把这个节点往下挪，直到它变为叶子为止，看图。

也许你要问，如果和左子树最大节点交换后，要删除的节点依然不是叶子，那怎么办呢？那继续呗，看图：

那左子树不存在的情况下呢？你可以查找右子树的最小节点，和上面是类似的，图我就不画了。

三、示例代码

 #include <iostream>
 #include <algorithm>
 using namespace std;
 #pragma once

 //平衡二叉树结点
 template <typename T>
 struct AvlNode
 {
     T data;
     int height; //结点所在高度
     AvlNode<T> *left;
     AvlNode<T> *right;
     AvlNode<T>(const T theData) : data(theData), left(NULL), right(NULL), height(){}
 };

 //AvlTree
 template <typename T>
 class AvlTree
 {
 public:
     AvlTree<T>(){}
     ~AvlTree<T>(){}
     AvlNode<T> *root;
     //插入结点
     void Insert(AvlNode<T> *&t, T x);
     //删除结点
     bool Delete(AvlNode<T> *&t, T x);
     //查找是否存在给定值的结点
     bool Contains(AvlNode<T> *t, const T x) const;
     //中序遍历
     void InorderTraversal(AvlNode<T> *t);
     //前序遍历
     void PreorderTraversal(AvlNode<T> *t);
     //最小值结点
     AvlNode<T> *FindMin(AvlNode<T> *t) const;
     //最大值结点
     AvlNode<T> *FindMax(AvlNode<T> *t) const;
 private:
     //求树的高度
     int GetHeight(AvlNode<T> *t);
     //单旋转 左
     AvlNode<T> *LL(AvlNode<T> *t);
     //单旋转 右
     AvlNode<T> *RR(AvlNode<T> *t);
     //双旋转 右左
     AvlNode<T> *LR(AvlNode<T> *t);
     //双旋转 左右
     AvlNode<T> *RL(AvlNode<T> *t);
 };

 template <typename T>
 AvlNode<T> * AvlTree<T>::FindMax(AvlNode<T> *t) const
 {
     if (t == NULL)
         return NULL;
     if (t->right == NULL)
         return t;
     return FindMax(t->right);
 }

 template <typename T>
 AvlNode<T> * AvlTree<T>::FindMin(AvlNode<T> *t) const
 {
     if (t == NULL)
         return NULL;
     if (t->left == NULL)
         return t;
     return FindMin(t->left);
 }

 template <typename T>
 int AvlTree<T>::GetHeight(AvlNode<T> *t)
 {
     if (t == NULL)
         return -;
     else
         return t->height;
 }

 //单旋转
 //左左插入导致的不平衡
 template <typename T>
 AvlNode<T> * AvlTree<T>::LL(AvlNode<T> *t)
 {
     AvlNode<T> *q = t->left;
     t->left = q->right;
     q->right = t;
     t = q;
     t->height = max(GetHeight(t->left), GetHeight(t->right)) + ;
     q->height = max(GetHeight(q->left), GetHeight(q->right)) + ;
     return q;
 }

 //单旋转
 //右右插入导致的不平衡
 template <typename T>
 AvlNode<T> * AvlTree<T>::RR(AvlNode<T> *t)
 {
     AvlNode<T> *q = t->right;
     t->right = q->left;
     q->left = t;
     t = q;
     t->height = max(GetHeight(t->left), GetHeight(t->right)) + ;
     q->height = max(GetHeight(q->left), GetHeight(q->right)) + ;
     return q;
 }

 //双旋转
 //插入点位于t的左儿子的右子树
 template <typename T>
 AvlNode<T> * AvlTree<T>::LR(AvlNode<T> *t)
 {
     //双旋转可以通过两次单旋转实现
     //对t的左结点进行RR旋转，再对根节点进行LL旋转
     RR(t->left);
     return LL(t);
 }

 //双旋转
 //插入点位于t的右儿子的左子树
 template <typename T>
 AvlNode<T> * AvlTree<T>::RL(AvlNode<T> *t)
 {
     LL(t->right);
     return RR(t);
 }

 template <typename T>
 void AvlTree<T>::Insert(AvlNode<T> *&t, T x)
 {
     if (t == NULL)
         t = new AvlNode<T>(x);
     else if (x < t->data)
     {
         Insert(t->left, x);
         //判断平衡情况
         if (GetHeight(t->left) - GetHeight(t->right) > )
         {
             //分两种情况 左左或左右

             if (x < t->left->data)//左左
                 t = LL(t);
             else                  //左右
                 t = LR(t);
         }
     }
     else if (x > t->data)
     {
         Insert(t->right, x);
         if (GetHeight(t->right) - GetHeight(t->left) > )
         {
             if (x > t->right->data)
                 t = RR(t);
             else
                 t = RL(t);
         }
     }
     else
         ;//数据重复
     t->height = max(GetHeight(t->left), GetHeight(t->right)) + ;
 }

 template <typename T>
 bool AvlTree<T>::Delete(AvlNode<T> *&t, T x)
 {
     //t为空 未找到要删除的结点
     if (t == NULL)
         return false;
     //找到了要删除的结点
     else if (t->data == x)
     {
         //左右子树都非空
         if (t->left != NULL && t->right != NULL)
         {//在高度更大的那个子树上进行删除操作

             //左子树高度大，删除左子树中值最大的结点，将其赋给根结点
             if (GetHeight(t->left) > GetHeight(t->right))
             {
                 t->data = FindMax(t->left)->data;
                 Delete(t->left, t->data);
             }
             else//右子树高度更大，删除右子树中值最小的结点，将其赋给根结点
             {
                 t->data = FindMin(t->right)->data;
                 Delete(t->right, t->data);
             }
         }
         else
         {//左右子树有一个不为空，直接用需要删除的结点的子结点替换即可
             AvlNode<T> *old = t;
             t = t->left ? t->left: t->right;//t赋值为不空的子结点
             delete old;
         }
     }
     else if (x < t->data)//要删除的结点在左子树上
     {
         //递归删除左子树上的结点
         Delete(t->left, x);
         //判断是否仍然满足平衡条件
         if (GetHeight(t->right) - GetHeight(t->left) > )
         {
             if (GetHeight(t->right->left) > GetHeight(t->right->right))
             {
                 //RL双旋转
                 t = RL(t);
             }
             else
             {//RR单旋转
                 t = RR(t);
             }
         }
         else//满足平衡条件 调整高度信息
         {
             t->height = max(GetHeight(t->left), GetHeight(t->right)) + ;
         }
     }
     else//要删除的结点在右子树上
     {
         //递归删除右子树结点
         Delete(t->right, x);
         //判断平衡情况
         if (GetHeight(t->left) - GetHeight(t->right) > )
         {
             if (GetHeight(t->left->right) > GetHeight(t->left->left))
             {
                 //LR双旋转
                 t = LR(t);
             }
             else
             {
                 //LL单旋转
                 t = LL(t);
             }
         }
         else//满足平衡性 调整高度
         {
             t->height = max(GetHeight(t->left), GetHeight(t->right)) + ;
         }
     }

     return true;
 }

 //查找结点
 template <typename T>
 bool AvlTree<T>::Contains(AvlNode<T> *t, const T x) const
 {
     if (t == NULL)
         return false;
     if (x < t->data)
         return Contains(t->left, x);
     else if (x > t->data)
         return Contains(t->right, x);
     else
         return true;
 }

 //中序遍历
 template <typename T>
 void AvlTree<T>::InorderTraversal(AvlNode<T> *t)
 {
     if (t)
     {
         InorderTraversal(t->left);
         cout << t->data << ' ';
         InorderTraversal(t->right);
     }
 }

 //前序遍历
 template <typename T>
 void AvlTree<T>::PreorderTraversal(AvlNode<T> *t)
 {
     if (t)
     {
         cout << t->data << ' ';
         PreorderTraversal(t->left);
         PreorderTraversal(t->right);
     }
 }

cpp

 #include "AvlTree.h"

 int main()
 {
     AvlTree<int> tree;
     int value;
     int tmp;
     cout << "请输入整数建立二叉树(-1结束)：" << endl;
     while (cin >> value)
     {
         if (value == -)
             break;
         tree.Insert(tree.root,value);
     }
     cout << "中序遍历";
     tree.InorderTraversal(tree.root);
     cout << "\n前序遍历:";
     tree.PreorderTraversal(tree.root);
     cout << "\n请输入要查找的结点：";
     cin >> tmp;
     if (tree.Contains(tree.root, tmp))
         cout << "已查找到" << endl;
     else
         cout << "值为" << tmp << "的结点不存在" << endl;
     cout << "请输入要删除的结点：";
     cin >> tmp;
     tree.Delete(tree.root, tmp);
     cout << "删除后的中序遍历：";
     tree.InorderTraversal(tree.root);
     cout << "\n删除后的前序遍历：";
     tree.PreorderTraversal(tree.root);
 }