MCMC算法深入理解

MCMC(Markov Chain Monte Carlo)，即马尔科夫链蒙特卡洛方法，是以马尔科夫平稳状态作为理论基础，蒙特卡洛方法作为手段的概率序列生成技术。

MCMC理论基础

如果转移矩阵为P的马尔科夫链平稳状态和我们研究的概率质量函数（概率密度函数）分布一致，那么我么从任意初始值开始，经过一定次数的概率转以后，后续的转移值组成的序列必然服从马尔科夫平稳状态分布，也就是服从我们研究的概率分布，这样就生成了我们研究的概率分布的模拟数据序列。

对于任意初始值X0，经过n次概率转移后，生成值符合平稳状态分布，并且后续概率转移始终符合平稳状态分布，所以我们可以认为从第n次开始的转移值序列符合平稳状态分布。数学表达如下

1、          初始值为X0，X0通过转移矩阵P生成马氏链序列。

2、          马氏链经过n次转移后达到平稳状态。

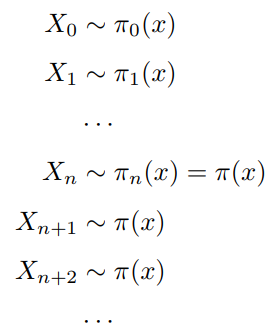
3、          则从第n次开始的转移序列符合平稳状态分布。

我们用城市化进程中人口转移模型来阐述一下这个思想的物理意义。我们假设第一代人为农村人。农村人下一代为农村人，第3代为城市人，城市人接下来9代为城市人，第10代为农村人（我们模拟农村人转化为城市人概率为0.5，城市人转化为农村人概率为0.1）。如下表，按照这种规律生成的随机序列农村人城市人比例为1:5，与之前计算的平稳分布17:83基本相等。实际上该模型下的马氏链平稳条件为：0.5 * 农村人 = 0.1 * 城市人，可以推测出农村人 : 城市人 =  1 : 5，与我们的模拟是一致的。

我们已经知道，使马尔科夫链的平稳状态等同于我们研究的概率分布，就可以构造出符合该概率分布的随机序列。现在的问题是如何构造出这样的马尔科夫链，使得其稳定分布等于我们研究的概率分布。

细致平稳条件

如下更强的马尔科夫链稳定状态定理可以解决这个问题

定义显而易见，从任意状态i转移到状态j的速率等于从状态j转移到状态i的速率，则状态转移稳定。城市化进程的例子充分说明了这一点。定理中π分布就是我们研究的概率分布，我们构造出P，则构造出了稳定状态满足π分布马尔科夫链。

算法实现

我们随机初始化一个转移矩阵Q（比如均匀分布），q(i, j)表示从状态i转移到状态j的概率。一般情况下Q显然不满足细致平稳条件，即

p(i)q(i, j) != p(j)q(j, i)

我们构造α(i, j)与α(j, i)，使等式成立，即

其中

α(i, j) = p(j)q(j, i) α(j, i) = p(i)q(i, j)

这样，我们通Q与α，构造了一个符合细致平稳条件的Q’。

Q一般来说是我们熟悉的概率分布，计算机易于模拟，但是Q’怎么模拟呢？在构造Q’的过程中，我们引入的α(i, j)称作接受率，我们生成一个符合Q分布的状态后，再以α(i, j)的概率来接受状态转移。（实际上q(j, i)α(i, j)就是转移矩阵Q’中状态i转移到j的概率，我们以α(i, j)接受状态转移就是在进行乘以转移矩阵Q’运算）

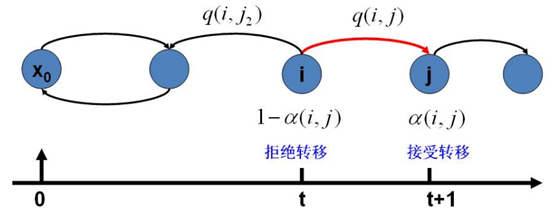
MCMC算法如下

上述算法还有一个小缺陷，接受率α(i, j)可能较小，导致状态转移概率太小，收敛较慢。实际上，对于细致平稳条件，等式两边同时乘以一个倍数，也是成立的。于是我们把细致平稳条件改造为

p(i)q(i, j) α(i, j)/ α(j, i) = p(j)q(j, i)

则可以用如下接受率进行状态转移

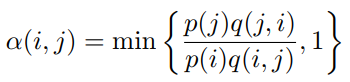
改进后的MCMC算法如下

参考：

https://www.jianshu.com/p/28d32aa7cc45

《LDA数学八卦》