POJ 1661 Help Jimmy（DP/最短路）

Help Jimmy

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 14980		Accepted: 4993

Description

"Help Jimmy" 是在下图所示的场景上完成的游戏。 
　
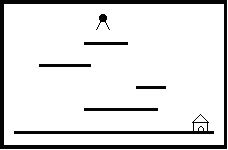
场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。

Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。

设计一个程序，计算Jimmy到底地面时可能的最早时间。 
　

Input

第一行是测试数据的组数t（0 <= t <=
20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1
<= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i =
1..N）。所有坐标的单位都是米。

Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。 
　

Output

对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。

Sample Input

1
3 8 17 20
0 10 8
0 10 13
4 14 3

Sample Output

23

Source

POJ Monthly--2004.05.15 CEOI 2000

　

【思路1】

最短路：

构图转化成求最短路。
　　 将每个平台看作两个点，即左端点和右端点，然后将符合条件的两点相连，边长即为两点之间的垂直距离和水平距离。
　　 将jimmy起始的地点看作顶点0，而地面看作顶点2*N+1，这样就是求0到2*N+1的单源最短路径。

要注意：
　　1.一开始做的时候，没仔细想，认为只要两个平台之间符合条件，就建立边的关系。
　　　忽略了一个平台下方最多只能有两个平台（即左端点下方一个，右端点下方一个）。也就是说一个点最多只能与一个点相连。
　　2.jimmy有可能可以直接落到地上
　　3.能与地面相连的点，必须保证它的下方没有阻隔的平台

【代码1】

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define pir pair<int,int>
using namespace std;
const int N=1010*2;
struct data{int l,r,h;}a[N];
int n,cnt,cas,sx,sy,maxn,f[N][2];
inline bool cmp(const data &b,const data &c){
	return b.h>c.h;
}
inline void Init(){
	cnt=0;
	scanf("%d%d%d%d",&n,&sx,&sy,&maxn);
	for(int i=1,x,y,z;i<=n;i++){
		scanf("%d%d%d",&x,&y,&z);
		if(z<=sy){
			a[++cnt].l=x;
			a[cnt].r=y;
			a[cnt].h=z;
		}
	}
	a[++cnt].l=sx,a[cnt].r=sx,a[cnt].h=sy;
	a[++cnt].l=-1e5,a[cnt].r=1e5,a[cnt].h=0;
	sort(a+1,a+cnt+1,cmp);
}
inline void Solve(){
	memset(f,0x3f,sizeof f);
	f[1][0]=f[1][1]=0;
	for(int i=1;i<=cnt;i++){
		int cnt1(0),cnt2(0);
		for(int j=i+1;j<=cnt;j++){
			int h=a[i].h-a[j].h;
			if(h<=maxn){
				if(a[j].l<=a[i].l&&a[i].l<=a[j].r){
					if(j==cnt){
						f[j][0]=min(f[j][0],f[i][0]+h);
						f[j][1]=min(f[j][1],f[i][0]+h);
					}
					else{
						f[j][0]=min(f[j][0],f[i][0]+h+a[i].l-a[j].l);
						f[j][1]=min(f[j][1],f[i][0]+h+a[j].r-a[i].l);
					}
					break;
				}
			}
		}
		for(int j=i+1;j<=cnt;j++){
			int h=a[i].h-a[j].h;
			if(h<=maxn){
				if(a[j].l<=a[i].r&&a[i].r<=a[j].r){
					if(j==cnt){
						f[j][0]=min(f[j][0],f[i][1]+h);
						f[j][1]=min(f[j][1],f[i][1]+h);
					}
					else{
						f[j][0]=min(f[j][0],f[i][1]+h+a[i].r-a[j].l);
						f[j][1]=min(f[j][1],f[i][1]+h+a[j].r-a[i].r);
					}
					break;
				}
			}
		}
	}
	printf("%d\n",min(f[cnt][0],f[cnt][1]));
}
int main(){
	for(scanf("%d",&cas);cas--;){
		Init();
		Solve();
	}
	return 0;
} 

【思路2】

动态规划：

f[i][0]表示到达第i个板子的左边最小距离
f[i][1]表示到达第i个板子的右边最小距离
多加两块板子，一块是起点，一块是地面，地面的范围为【-inf，inf】

你从上一块的板子的一端走，你可以走到下一块板子的右边 也可以是左边。
转移方程详见代码

【代码2】

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define pir pair<int,int>
using namespace std;
const int N=1010*2;
int n,cas,sx,sy,maxn,S,T,dis[N];
struct data{int l,r,h;}a[N];
struct node{int v,w,next;}e[N*N];int tot,head[N];bool vis[N];
inline void addedge(int x,int y,int z){
	e[++tot].v=y;e[tot].w=z;e[tot].next=head[x];head[x]=tot;
}
inline void add(int x,int y,int z){
	addedge(x,y,z);
	addedge(y,x,z);
}
inline void Clear(){
	tot=0;
	memset(head,S,sizeof head);
	memset(vis,S,sizeof vis);
	memset(dis,0x3f,sizeof dis);
}
inline void Init(){
	scanf("%d%d%d%d",&n,&sx,&sy,&maxn);
	for(int i=1;i<=n;i++) scanf("%d%d%d",&a[i].l,&a[i].r,&a[i].h);
}
#define mp make_pair
inline void dijkstra(){
	priority_queue<pir,vector<pir>,greater<pir> >q;
	q.push(mp(dis[S]=0,S));
	while(!q.empty()){
		pir t=q.top();q.pop();
		int x=t.second;
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=head[x];i;i=e[i].next){
			int v=e[i].v;
			if(!vis[v]&&dis[v]>dis[x]+e[i].w){
				q.push(mp(dis[v]=dis[x]+e[i].w,v));
			}
		}
	}
	printf("%d\n",dis[T]);
}
inline bool cmp(const data &b,const data &c){
	return b.h>c.h;
}
#define L(x) (x)
#define R(x) (x+n)
inline void Graph(){
	S=0,T=n<<1|1;
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++){
		int cnt1(0),cnt2(0);
		for(int j=i+1;j<=n;j++){
			if(a[j].l<=a[i].l&&a[j].r>=a[i].l&&a[i].h-a[j].h>=0&&a[i].h-a[j].h<=maxn){
				if(++cnt1==1){
					add(L(i),L(j),a[i].h-a[j].h+a[i].l-a[j].l);
					add(L(i),R(j),a[i].h-a[j].h+a[j].r-a[i].l);
				}
			}
			if(a[j].l<=a[i].r&&a[j].r>=a[i].r&&a[i].h-a[j].h>=0&&a[i].h-a[j].h<=maxn){
				if(++cnt2==1){
					add(R(i),L(j),a[i].h-a[j].h+a[i].r-a[j].l);
					add(R(i),R(j),a[i].h-a[j].h+a[j].r-a[i].r);
				}
			}
		}
		if(!cnt1&&a[i].h<=maxn) add(L(i),T,a[i].h);
		if(!cnt2&&a[i].h<=maxn) add(R(i),T,a[i].h);
	}
	int cnt(0);
	for(int i=1;i<=n;i++){
		if(a[i].l<=sx&&sx<=a[i].r&&sy-a[i].h>=0&&sy-a[i].h<=maxn){
			if(++cnt==1){
				add(S,L(i),sy-a[i].h+sx-a[i].l);
				add(S,R(i),sy-a[i].h+a[i].r-sx);
			}
		}
	}
	if(!cnt) add(S,T,sy);
}
inline void Solve(){
	Graph();
	dijkstra();
}
int main(){
	for(scanf("%d",&cas);cas--;){
		Clear();
		Init();
		Solve();
	}
	return 0;
}