NOIp模拟赛 现实(DP 拓扑)

题目来源：by lzz

\(Description\)

　　给定一张有向图，求对于哪些点，删除它和它的所有连边后，图没有环。

　　\(n\leq 5\times10^5,m\leq 10^6\)。

\(Solution\)

　　题目等价于求所有环的交集。

　　首先两个特判：如果原图没有环，输出所有点；如果删掉原图的某个环后，仍存在环，输出\(0\)。这也是不少分了。

　　先求出图中的某个环，环交当然在这个环上。我们只需要处理这个环。

　　把环拆成链，发现所有除它外的环只有两种情况：



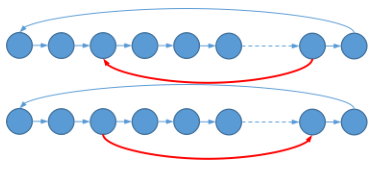
　　对于第一种情况，





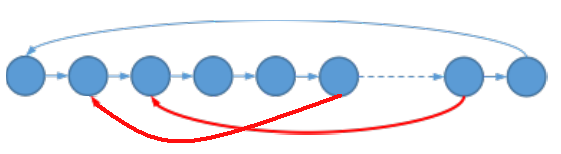
　　如果做过这个链的Subtask，很容易发现（倒也显然）合法的点只可能是这些环的交集（把红边看成线段，就是求区间的交）。之前的第二次判环可以拓扑，然后利用拓扑序从出度为0的点更新能到它的点的最左位置\(pl\)、从入度为0的点更新它到的点的最右位置\(pr\)。然后就可以找到最右的左端点和最靠左的右端点。

　　对于第二种情况，



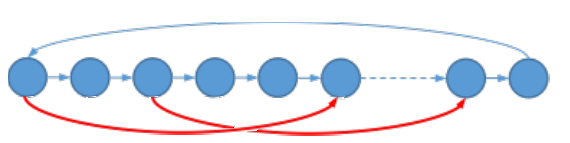
　　显然，如果存在红边\(x\rightarrow y\)，则\(x,y\)之间的点都不是合法的。

　　依旧利用拓扑序从出度为0的点更新到它的点的最右位置\(pr\)，然后扫一遍。

　　两种情况都合法的点就是答案了。

　　发现图中只有两个环，且环交为1个点时，这个点是合法的，但是删掉环边后图仍存在环，会返回无解。我们发现如果将每个点拆成入点和出点，这种情况就可以处理了。即把环交从点集变成边集。

　　复杂度\(O(n+m)\)。

#include <cstdio>
#include <cctype>
#include <vector>
#include <cstring>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
const int N=1e6+5,M=1e6+5+N;

int n,m,Enum,H[N],nxt[M],to[M],dgr[N],cir[N],sz,pre[N],fa[N],q[N],pl[N],pr[N];
bool find_circle,vis[N],ins[N],isc[M],ok[N];
std::vector<int> ans;
char IN[MAXIN],*SS=IN,*TT=IN;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline void AE(int v,int u)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum;
}
void DFS(int x)
{
	vis[x]=ins[x]=1;
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]])
		{
			fa[v]=x, pre[v]=i, DFS(v);
			if(find_circle) return;
		}
		else if(ins[v])
		{
			for(int p=x; p!=v; p=fa[p]) cir[++sz]=p, isc[pre[p]]=1;
			cir[++sz]=v, isc[i]=1;
			std::reverse(cir+1,cir+1+sz);
			find_circle=1; return;
		}
	ins[x]=0;
}
bool Toposort()
{
	int h=0,t=0;
	for(int i=1; i<=Enum; ++i) if(!isc[i]) ++dgr[to[i]];//度也是删环后的！
	for(int i=1; i<=n; ++i) if(!dgr[i]) q[t++]=i;
	while(h<t)
	{
		int x=q[h++];
		for(int i=H[x]; i; i=nxt[i])
			if(!isc[i] && !--dgr[to[i]]) q[t++]=to[i];
	}
	return t==n;
}
void Solve()
{
	for(int i=1; i<=n; ++i)
		if(!vis[i]) {DFS(i); if(find_circle) break;}
	if(!find_circle)
	{
		n>>=1;
		for(int i=1; i<=n; ++i) ans.push_back(i);
		return;
	}
	if(!Toposort()) return;

	int ansl=1,ansr=sz;
	for(int i=1; i<=sz; ++i) pl[cir[i]]=pr[cir[i]]=i;
	for(int i=n,x; i; --i)
	{
		if(!pl[x=q[i]]) pl[x]=N;//避免环外的影响
		for(int j=H[x]; j; j=nxt[j])
			if(!isc[j]/*!*/) pl[x]=std::min(pl[x],pl[to[j]]);//非环边！又忘判了
	}
	for(int i=1; i<=sz; ++i)
		if(pl[cir[i]]<i) {ansr=i; break;}//对于左端端点应该有pl[i]==i
	for(int i=1,x; i<=n; ++i)
	{
//		if(!pr[x=q[i]]) pr[x]=0;
		for(int j=H[x=q[i]]; j; j=nxt[j])
			if(!isc[j]) pr[to[j]]=std::max(pr[to[j]],pr[x]);
	}
	for(int i=sz; i; --i)
		if(pr[cir[i]]>i) {ansl=i; break;}
	if(ansl>ansr) return;

	memset(pr,0,sizeof pr);
	for(int i=1; i<=sz; ++i) pr[cir[i]]=i;
	for(int i=n,x; i; --i)//对另一个方向的pr再求一次
	{
//		if(!pr[x=q[i]]) pr[x]=0;
		for(int j=H[x=q[i]]; j; j=nxt[j])
			if(!isc[j]) pr[x]=std::max(pr[x],pr[to[j]]);
	}
	int nowr=0;
	for(int i=1; i<=sz; ++i)
	{
		if(i>=nowr) ok[i]=1;
		nowr=std::max(nowr,pr[cir[i]]);
	}
	for(int i=ansl; i<ansr; i+=2) if(ok[i]) ans.push_back(cir[i]);//ansl一定是个入点
	std::sort(ans.begin(),ans.end());
}

int main()
{
	n=read();
	for(int i=1; i<=n; ++i) AE(i+n,i);//in:x out:x+n 参数顺序！
	for(int m=read(); m--; AE(read(),read()+n));
	n<<=1, Solve();
	printf("%d\n",ans.size());
	for(int i=0,l=ans.size(); i<l; ++i) printf("%d ",ans[i]);

	return 0;
}