bzoj4144【AMPPZ2014】Petrol

---

• 题解：

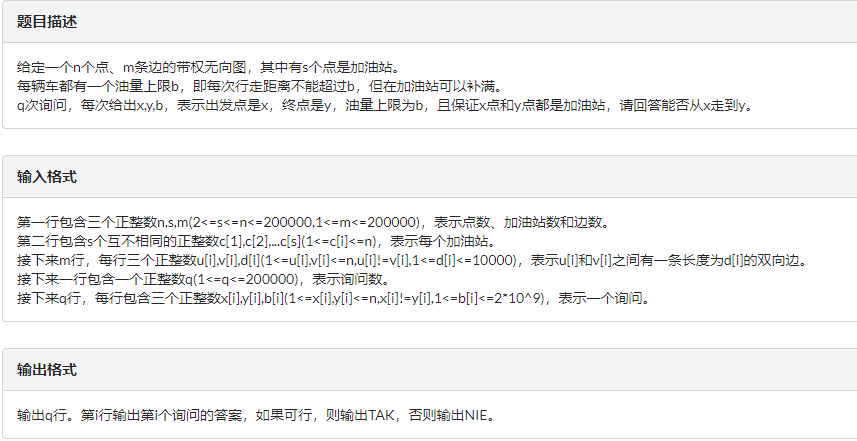
 首先注意到起点和终点都是加油站;

         假设中途经过某个非加油站的点u，u连到v，离u最近的加油站是x，那么从u到x加油后回到u，再到v一定不比直接从u到v差；

       因为u一定从某个加油站来，设最后经过的加油站为y，u点油量为B1 = b - dis(y,u)，而如果u不可以走到x一定不能走到其他任何加油站自然也到不了终点，如果可以到x加满油也一定可以再从x回来，油量为B2 = b-dis(x,u)  ， 因为dis(y,u) >= dis(x,u)所以B1 <= B2 ;

       考虑重新构图：nr[x]表示离x最近的加油站，dis[x]表示x和nr[x]的距离，可以用多源点dijkstra处理出所有nr[x]和dis[x];

       对于原图中边(u,v) 连边(nr[u] , nr[v] , dis[u] + dis[v] + w(u,v)   ) ;

       这就变成了一个图，只选<=b 的边问两点连通性，可以离线或者用kruskal重构树做；

---

 #include<bits/stdc++.h>
 #define mk make_pair
 #define fir first
 #define sec second
 using namespace std;
 const int N=;
 int n,m,k,s,c[N],dis[N],nr[N],vis[N],fa[N],o,hd[N],cnt,ans[N];
 struct Edge{int u,v,nt,w;}E[N<<],e[N],Q[N];
 void adde(int u,int v,int w){
     E[o]=(Edge){u,v,hd[u],w};hd[u]=o++;
     E[o]=(Edge){v,u,hd[v],w};hd[v]=o++;
 }
 typedef pair<int,int> pii;
 priority_queue<pii,vector<pii>,greater<pii> > q;
 void dijkstra(){
     memset(dis,0x3f,sizeof(dis));
     for(int i=;i<=s;i++)q.push(mk(dis[c[i]]=,c[i])),nr[c[i]]=c[i];
     while(!q.empty()){
         int u=q.top().sec;q.pop();
         if(vis[u])continue;
         vis[u]=;
         for(int i=hd[u];~i;i=E[i].nt){
             int v=E[i].v;
             if(dis[v]>dis[u]+E[i].w){
                 dis[v]=dis[u]+E[i].w;
                 nr[v]=nr[u];
                 if(!vis[v])q.push(mk(dis[v],v));
             }
         }
     }
 }
 bool cmp(const Edge&A,const Edge&B){return A.w<B.w;}
 int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
 int main(){
     freopen("bzoj4144.in","r",stdin);
     freopen("bzoj4144.out","w",stdout);
     memset(hd,-,sizeof(hd));
     scanf("%d%d%d",&n,&s,&m);
     for(int i=;i<=s;i++)scanf("%d",&c[i]);
     for(int i=;i<=m;i++){
         int u,v,w;
         scanf("%d%d%d",&u,&v,&w);
         adde(u,v,w);
     }
     scanf("%d",&k);
     for(int i=;i<=k;i++){scanf("%d%d%d",&Q[i].u,&Q[i].v,&Q[i].w),Q[i].nt=i;}
     dijkstra();
     for(int i=;i<o;i+=){
         int u=E[i].u,v=E[i].v;
         if(nr[u]!=nr[v])e[++cnt]=(Edge){nr[u],nr[v],,E[i].w+dis[u]+dis[v]};
     }
     for(int i=;i<=n;i++)fa[i]=i;
     sort(e+,e+cnt+,cmp);
     sort(Q+,Q+k+,cmp);
     for(int i=,j=;i<=k;i++){
         while(j<=cnt&&e[j].w<=Q[i].w){
             int fx=find(e[j].u),fy=find(e[j].v);
             if(fx!=fy)fa[fx]=fy;
             j++;
         }
         ans[Q[i].nt] = find(Q[i].u)==find(Q[i].v);
     }
     for(int i=;i<=k;i++){puts(ans[i]?"TAK":"NIE");}
     return ;
 }

bzoj4144