bzoj千题计划264：bzoj3884: 上帝与集合的正确用法

http://www.lydsy.com/JudgeOnline/problem.php?id=3884

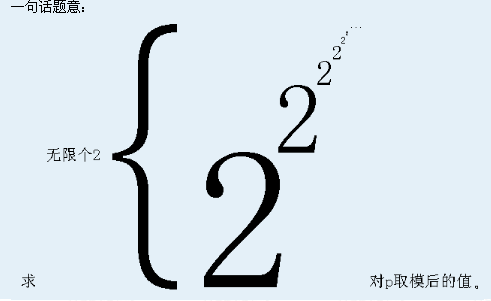
欧拉降幂公式

#include<cmath>
#include<cstdio>

using namespace std;

int get_phi(int p)
{
    int phi=p;
    int m=sqrt(p);
    for(int i=;i<=m;++i)
        if(p%i==)
        {
            phi=phi/i*(i-);
            while(p%i==) p/=i;
        }
    if(p>) phi=phi/p*(p-);
    return phi;
}

int Pow(int a,int b,int p)
{
    int res=;
    for(;b;a=1LL*a*a%p,b>>=)
        if(b&) res=1LL*res*a%p;
    return res;
}

int f(int p)
{
    if(p==) return ;
    int phi=get_phi(p);
    return Pow(,f(phi)+phi,p);
}

int main()
{
    int T,P;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&P);
        printf("%d\n",f(P));
    }
}