CS229 6.1 Neurons Networks Representation

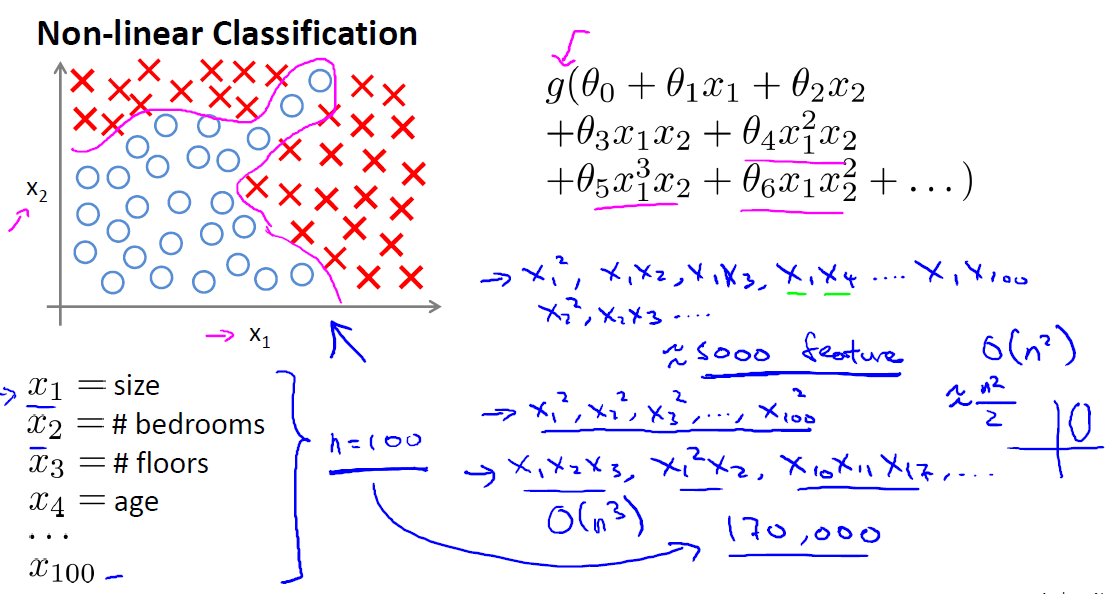
面对复杂的非线性可分的样本是，使用浅层分类器如Logistic等需要对样本进行复杂的映射，使得样本在映射后的空间是线性可分的，但在原始空间，分类边界可能是复杂的曲线。比如下图的样本只是在2维情形下的示例，假设有100维度，即特征数目是100，若使用logistic来做分类，对于这种线性不可分的情形，要对特征进行各种形式的组合映射，然后用映射后扩充的特征进行分类，可能会增加大量的参数，计算复杂性可想而知，而且可能会造成严重的over-fitting，可见logistic分类的局限性，下面引入NN。

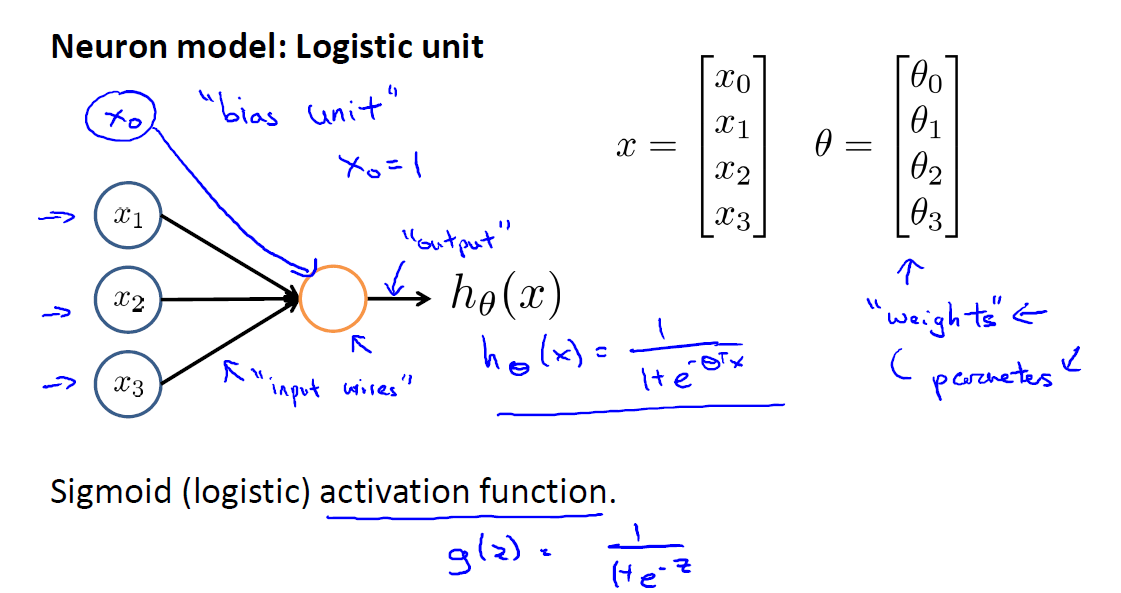
如下是一个单层网络的示意图，类似于感知机分类器，下图有三个feature，有一个bias unit，其值始终为1，对应的参数为ϴ₀ ϴ₁ ϴ₂ ϴ₃，最后其线性组合做一个sigmod映射来得到最终的结果

下图为含有隐藏层的Neurons Networds,a_i^(j)中的j表示层数，i表示第 i 个unit，ϴ^(j)示层j到j+1的参数矩阵ϴ_ij表示前一层的单元j到本层单元i的参数，本示例中ϴ⁽¹⁾为3*4的矩阵

更简洁的表示方法，把上一层的输入表示为z⁽ⁱ⁾, 下图中的z⁽²⁾ 分别表示上一层的activation，这三个值乘以对应的参数，然后做一个sigmod映射之后又可以当下一层的输入，最终我们的H_ϴ(x)=g(ϴ⁽²⁾*a⁽²⁾),可见最后我们不是对初始特征x₁ x₂ x₃做的运算，这可以理解为 Neurons Networks会自动组合特征，从而达到更好的效果。

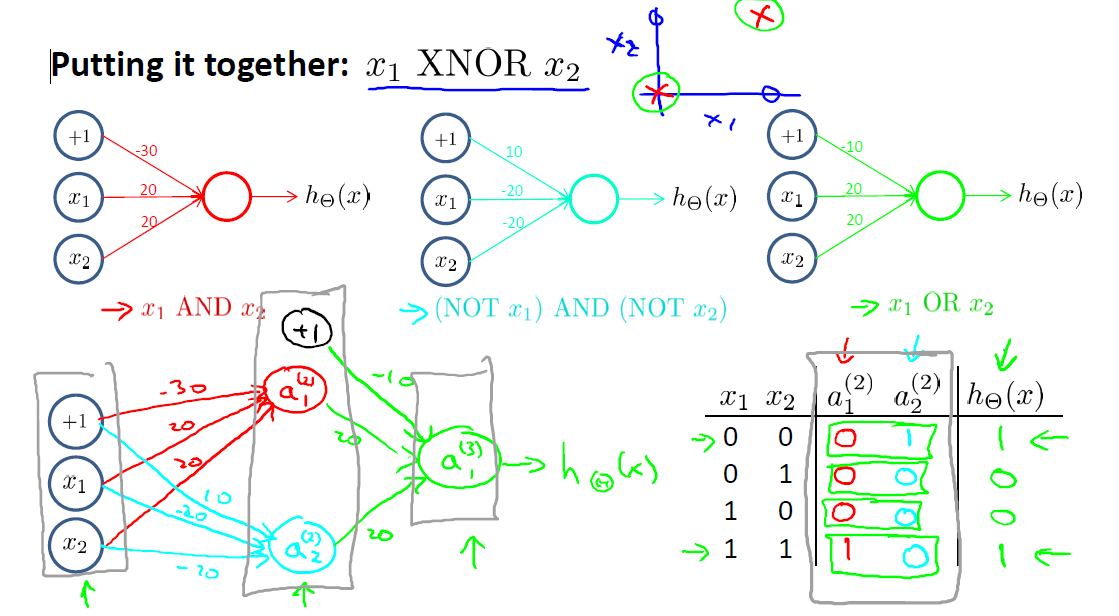
最后只得注意的是，对于非线性可分的情况，NN也可以进行分类，比如XOR（异或）的情况：