Kmeans原理与实现

原理

http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html

实现

http://www.cnblogs.com/zjutzz/p/5924762.html

无监督学习之K-均值算法分析与MATLAB代码实现

转载 https://blog.csdn.net/liweibin1994/article/details/77898341

前言

K-均值是一种无监督的聚类算法。首先我们要知道什么是无监督，无监督就是说在数据集中，数据是没有标签的。在有监督的数据集中，数据的形式可能是这样：{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}。而在无监督的数据集中，数据的形式是：{x(1),x(2),...,x(m)}{x(1),x(2),...,x(m)}。所谓的标签，就是有没有y。

无监督学习一般用来做什么呢？比如市场分割，也许在你的数据库中有很多用户的数据，你希望将用户分成不同的客户群，这样对不同类型的客户你可以分别提供更合适的服务。再比如图片压缩，假如图片有256种颜色，我们想用16种来表示，那么我们也可以用聚类的方式来将256种颜色分成16类。

K-均值算法

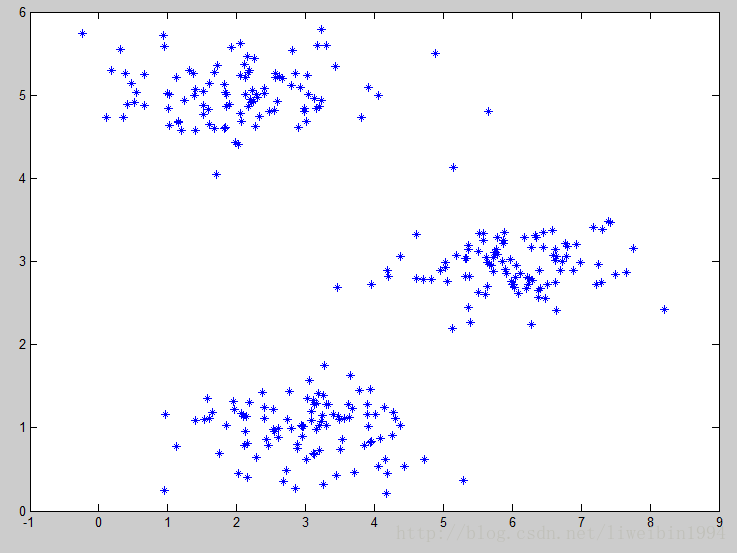
而K-均值是一个很普遍的聚类算法。这个算法接受一个未标记的数据集，然后将数据集聚类成不同的组。 

如上图所示，我们可以很直观地看出数据集大致可以分成三类，K-均值算法的思想就是选择三个随机的点(当然，分成K类就K个随机的点)，称为聚类中心(cluster centroids)。

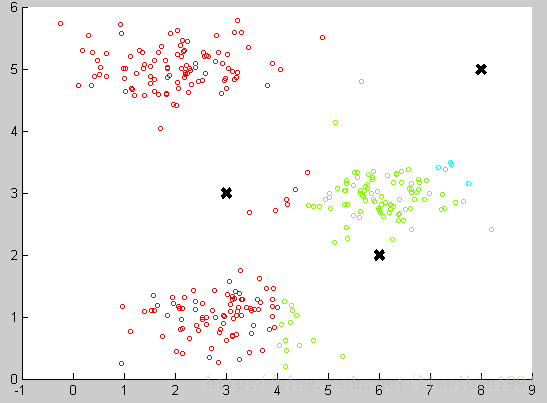
然后对于数据集中的每一个数据，按照距离三个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。如下图： 

图中三个黑色的点就是三个聚类中心，数据集也根据与聚类中心的远近分成三组。可以看出，此时的分类还是不好的。那么我们接下来应该怎么做才能让这个分类效果更好呢？

我们可以计算每个组(数据集被分成红绿蓝这三个组)的数据的平均值，将该组所关联的中心点移动到平均值的位置。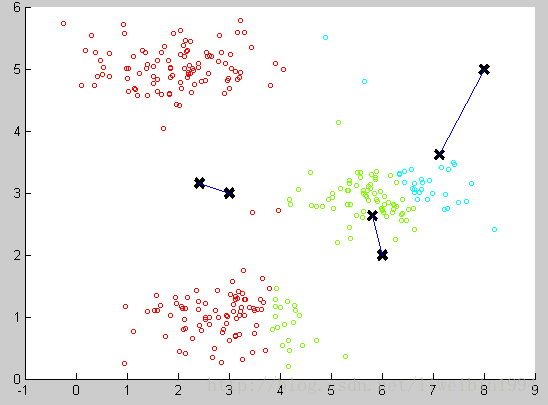 
 
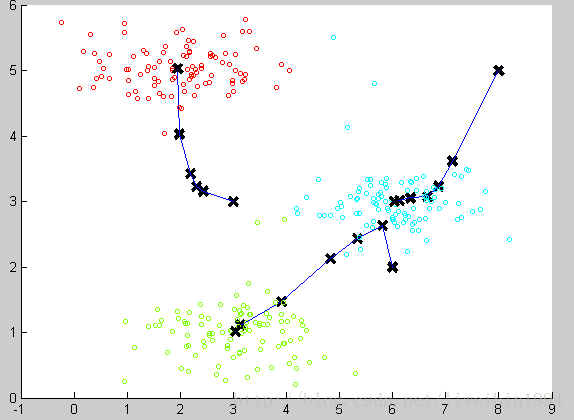
通过计算平均值，将聚类中心移动到平均值所在的位置，然后我们重复这个过程，直到中心点不再变化。最后就可以得到下面的效果： 

可以看到聚类的效果还不错。

算法步骤与伪代码

根据上面的分析，算法的步骤可以归结为： 
第一步，随机选择三个点，假设为A，B，C；

第二步：计算数据集中的每个数据x(i)x(i)分别到A，B，C的距离，这样每个数据就能计算出三个距离，哪个距离小，该数据就属于哪个聚类中心。最后就会得到三组类别的数据。

第三步，计算三组类别的数据的均值，分别作为A，B，C的新位置。

第四步，重复第二步和第三步直到迭代结束或者A，B，C的位置不再移动。

K-均值的伪代码如下： 
用μ1,μ2,...,μKμ1,μ2,...,μK来表示聚类中心，用c(1),c(2),...,c(m)c(1),c(2),...,c(m)来存储于第i个训练数据最近的聚类中心的索引(即从1到K的某一个数)，

Repeat{ 
for i=1 to m 
c(i)c(i) := index(from 1 to K )of cluster centroid closest to x(i)x(i)

for k = 1 to K 
μkμk := average(mean) of points assigned to cluster k 
}

优化目标（代价函数）

K-均值最小化问题，是要最小化所有的数据点与其关联的聚类中心之间的距离之和。因此，K-均值的代价函数：

 

J(c(1),c(2),...,c(m),μ1,μ2,...,μK)=1m∑i=1m∥∥x(i)−μc(i)∥∥2J(c(1),c(2),...,c(m),μ1,μ2,...,μK)=1m∑i=1m‖x(i)−μc(i)‖2

其中，μc(i)μc(i)代表与x(i)x(i)最近的聚类中心点。我们的优化目标就是要找到使得代价函数最小的c(1),c(2),...,c(m)c(1),c(2),...,c(m)和μ1,μ2,...,μKμ1,μ2,...,μK。

上面的伪代码中，第一个for循环就是用于减少c(i)c(i)引起的代价，因为在第一个循环中，聚类中心是不变的，所以要求数据都去找最近的聚类中心，这样总的距离才是最小的。

第二个循环则是用于减小μiμi引起的代价，因为这里改变的是聚类中心的位置，而数据的类别不变，所以要求聚类中心尽可能在其所属数据的中心。

初始化问题

在上面的步骤分析中，运行K-均值算法之前，我们首先要随机初始化所有的聚类中心。如何初始化比较好呢？

1. 首先，应该选择K < m，也就是聚类中心的个数要小于所有训练集实例的数量。
2. 随机选择K个训练样本，然后令K个聚类中心分别与这K个训练样本相等。

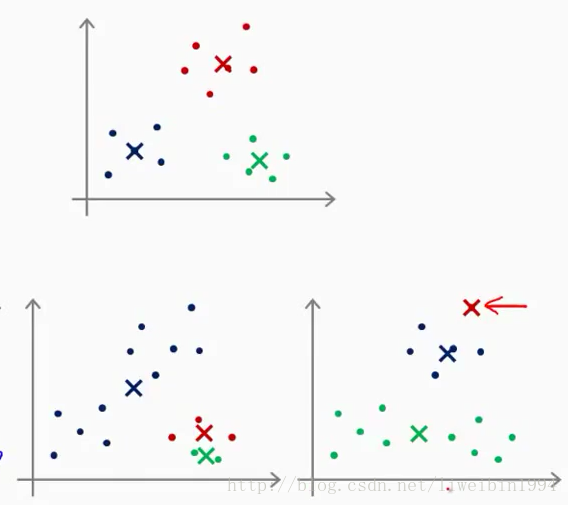
上面一开始说随机取K个点这种做法其实不推荐。K-均值的一个问题就在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。 

图中上面一个坐标系是分类正常，下面两个都是分类不好的情况。为了解决这个问题，我们通常需要多次运行K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值的结果，选择代价函数最小的结果。这种方法在K较小的时候(2~10)还是可行的，但是如果K较大，这么做也可能不会有明显的效果。

K的选择

其实没有所谓的最好的选择聚类数K的方法，通常是根据不同的问题，人工进行选择的。选择的时候思考我们运用K-均值算法聚类的动机是什么，然后选择能最好服务于该目的的聚类数。

肘部法则

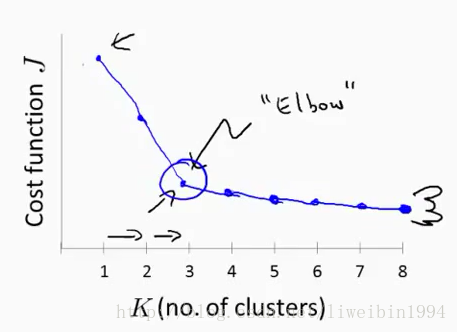
一般来说，人们可能会用肘部法则来选择K。这个法则的做法就是改变K值，然后每次改变之后我们运行一下算法，得到代价函数J的值，然后画图像： 

横坐标是K的数量，纵坐标是代价J。经过上面的做法我们可能会得到图中所示的曲线。这条曲线像人的肘部，所以叫肘部法则。在这种模式下(曲线下)，随着K的增加，代价函数的值会迅速减小，然后趋于平缓。所以我们一般就会选择拐点对应的K值来作为聚类数。

MATLAB代码

matlab的代码已经放在GitHub上面了。