POJ-1410

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 12817		Accepted: 3343

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
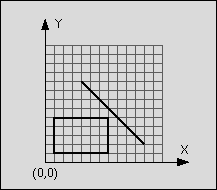
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

Source

Southwestern European Regional Contest 1995

题意：给一条线段，然后是一个矩形，问线段是否与矩形相交

　　　　kuangbin模版

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <cmath>
#define eps 1e-8
#define maxn 100
using namespace std;
int sgn(double x)
{
    if(abs(x) < eps) return ;
    if(x<) return -;
    else return ;
}
struct Point
{
    double x;
    double y;
    Point(){}
    Point(double _x,double _y)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &a) const
    {
        return Point(x-a.x,y-a.y);
    }
    Point operator + (const Point &a) const
    {
        return Point(x+a.x,y+a.y);
    }
    double  operator *(const Point &a) const
    {
        return x*a.x+y*a.y;
    }
    double  operator ^(const Point &a) const
    {
        return x*a.y-y*a.x;
    }
};
struct Line
{
    Point s;
    Point e;
    Line(){}
    Line(Point _s,Point _e)
    {
        s = _s;
        e = _e;
    }
};
///判断线段相交
bool inter(Line l1,Line l2)
{
    return
    max(l1.s.x,l1.e.x) >= min(l2.s.x,l2.e.x) &&
    max(l2.s.x,l2.e.x) >= min(l1.s.x,l1.e.x) &&
    max(l1.s.y,l1.e.y) >= min(l2.s.y,l2.e.y) &&
    max(l2.s.y,l2.e.y) >= min(l1.s.y,l1.e.y) &&
    sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s-l1.e)) <= &&
    sgn((l1.s-l2.e)^(l2.s-l2.e))*sgn((l1.e-l2.e)^(l2.s-l2.e)) <=;
}
///判断直线和线段是否相交
bool seg_inter_line(Line l1,Line l2)
{
    return sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s,l1.e)) <=;
}
bool Onseg(Point p,Line L)
{
    return
    sgn((L.s-p)^(L.e-p)) ==  &&
    sgn((p.x-L.s.x)*(p.x-L.e.x)) <=  &&
    sgn((p.y-L.s.y)*(p.y-L.e.y)) <= ;
}
int inConvexpoly(Point a,Point p[],int n)
{
    for(int i=;i<n;i++)
    {
        if(sgn((p[i]-a)^(p[(i+)%n]-a)) < ) return -;
        else if(Onseg(a,Line(p[i],p[(i+)%n]))) return ;
    }
    return ;
}
int main()
{
    //freopen("in.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        Point s;
        Point e;
        double  x1,y1,x2,y2;
        scanf("%lf %lf %lf %lf %lf %lf %lf %lf",&s.x,&s.y,&e.x,&e.y,&x1,&y1,&x2,&y2);
        if(x1 > x2) swap(x1,x2);
        if(y1 > y2) swap(y1,y2);
        Point p[];
        Line L = Line(s,e);
        p[] = Point(x1,y1);
        p[] = Point(x2,y1);
        p[] = Point(x2,y2);
        p[] = Point(x1,y2);
        if(inter(L,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        else if(inter(L,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        else if(inter(L,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        else if(inter(L,Line(p[],p[])))
        {
            printf("T\n");
            continue;
        }
        else if(inConvexpoly(L.s,p,)>= || inConvexpoly(L.e,p,)>=)
        {
             printf("T\n");
            continue;
        }
        else
            printf("F\n");
    }
    return ;
}