视觉SLAM：VIO的误差和误差雅可比矩阵

1.两个相机之间的非线性优化

观测相机方程关于相机位姿与特征点的雅可比矩阵：

1.1 位姿：



1.2 3D特征点

• fx,fy,fz为相机内参
• X',Y',Z'为3D点在相机坐标系下的坐标
• 该误差是观测值减去预测值，反过来，预测值减观测值时，去掉或加上负号即可
• 姿态定义为先平移后旋转，如果定义为先旋转后平移，将该矩阵的前3列与后3列对调即可

2.vio滑动窗口的BA优化

1.相机：

相机误差仍然为重投影误差：

优化是在机体坐标系下完成，也就是imu系，所以多了一个相机到机体坐标的外参

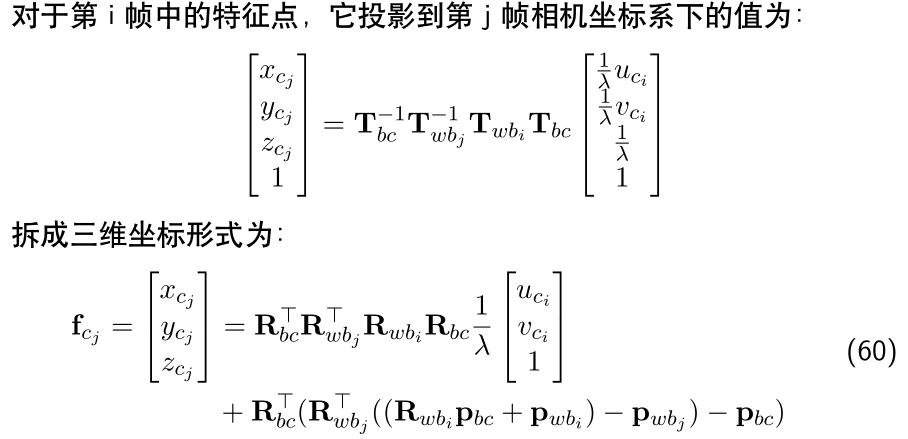
根据链式法则，可以分两步走，第一步，误差对\(f_{cj}\)求导，最后再分别相乘即可

2.1 误差对\(f_{cj}\)求导：

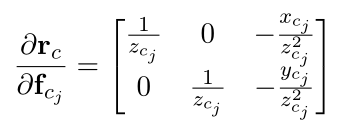
2.2 \(f_{cj}\)对逆深度的求导：

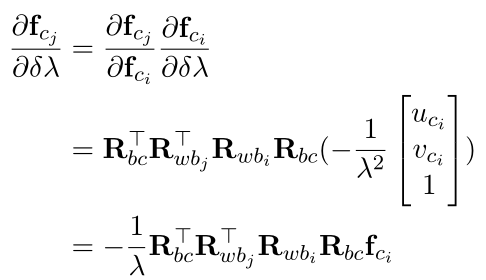
2.3 \(f_{cj}\)对各时刻状态量的求导：

• 对i时刻的位移求导：
  
  
  
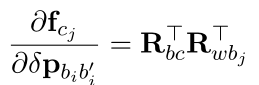
  对i时刻的角度增量求导：
  
  

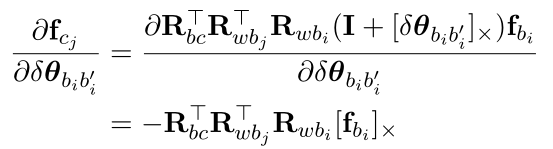
• 对j时刻的位移求导;
  
  
  
  对j时刻的角度增量求导
  
  

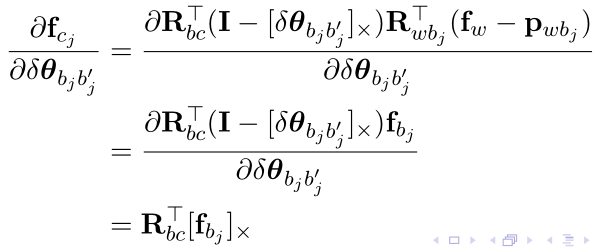
2.4 \(f_{cj}\)对imu和相机的外参求导：

• 对位移求导：
  
  
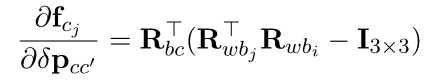
• 对角度增量求导：
  
  分为两部分求导： \(f_{cj} = f_{cj}^{1} + f_{cj}^{2}\)
  
  第一部分：
  
  
  
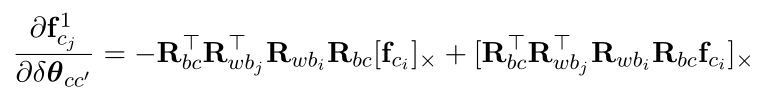
  第二部分：
  
  
  
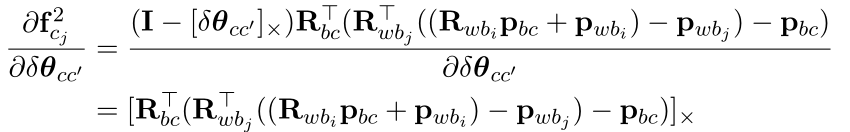
  最后相加即可。

注意：最后别忘了分别乘上误差对\(f_{cj}\)的求导

2.5 程序示例：

double inv_dep_i = verticies_[0]->Parameters()[0];

    VecX param_i = verticies_[1]->Parameters();  //i时刻位姿
    Qd Qi(param_i[6], param_i[3], param_i[4], param_i[5]); //姿态
    Vec3 Pi = param_i.head<3>();  //位移

    VecX param_j = verticies_[2]->Parameters();  //j时刻位姿
    Qd Qj(param_j[6], param_j[3], param_j[4], param_j[5]);
    Vec3 Pj = param_j.head<3>();

    VecX param_ext = verticies_[3]->Parameters();
    Qd qic(param_ext[6], param_ext[3], param_ext[4], param_ext[5]);
    Vec3 tic = param_ext.head<3>()

    Vec3 pts_camera_i = pts_i_ / inv_dep_i;
    Vec3 pts_imu_i = qic * pts_camera_i + tic;
    Vec3 pts_w = Qi * pts_imu_i + Pi;
    Vec3 pts_imu_j = Qj.inverse() * (pts_w - Pj);
    Vec3 pts_camera_j = qic.inverse() * (pts_imu_j - tic);

    double dep_j = pts_camera_j.z();   

    Mat33 Ri = Qi.toRotationMatrix();
    Mat33 Rj = Qj.toRotationMatrix();
    Mat33 ric = qic.toRotationMatrix();
    Mat23 reduce(2, 3);        //误差对f_cj求导
    reduce << 1. / dep_j, 0, -pts_camera_j(0) / (dep_j * dep_j),
        0, 1. / dep_j, -pts_camera_j(1) / (dep_j * dep_j);
//    reduce = information_ * reduce;

    Eigen::Matrix<double, 2, 6> jacobian_pose_i;
    Eigen::Matrix<double, 3, 6> jaco_i;
    jaco_i.leftCols<3>() = ric.transpose() * Rj.transpose(); //位移求导
    jaco_i.rightCols<3>() = ric.transpose() * Rj.transpose() * Ri * -
Sophus::SO3d::hat(pts_imu_i); //角度增量求导
    jacobian_pose_i.leftCols<6>() = reduce * jaco_i;

    Eigen::Matrix<double, 2, 6> jacobian_pose_j;
    Eigen::Matrix<double, 3, 6> jaco_j;
    jaco_j.leftCols<3>() = ric.transpose() * -Rj.transpose();
    jaco_j.rightCols<3>() = ric.transpose() * Sophus::SO3d::hat(pts_imu_j);
    jacobian_pose_j.leftCols<6>() = reduce * jaco_j;

    Eigen::Vector2d jacobian_feature;
    //逆深度求导
    jacobian_feature = reduce * ric.transpose() * Rj.transpose() * Ri * ric * pts_i_ * -1.0 / (inv_dep_i * inv_dep_i);

    //IMU和相机外参求导
    Eigen::Matrix<double, 2, 6> jacobian_ex_pose;
    Eigen::Matrix<double, 3, 6> jaco_ex;
    jaco_ex.leftCols<3>() = ric.transpose() * (Rj.transpose() * Ri - Eigen::Matrix3d::Identity());
    Eigen::Matrix3d tmp_r = ric.transpose() * Rj.transpose() * Ri * ric;
    jaco_ex.rightCols<3>() = -tmp_r * Utility::skewSymmetric(pts_camera_i) + Utility::skewSymmetric(tmp_r * pts_camera_i) + Utility::skewSymmetric(ric.transpose() * (Rj.transpose() * (Ri * tic + Pi - Pj) - tic));

    jacobian_ex_pose.leftCols<6>() = reduce * jaco_ex;

    jacobians_[0] = jacobian_feature;   //2行1列
    jacobians_[1] = jacobian_pose_i;
    jacobians_[2] = jacobian_pose_j;
    jacobians_[3] = jacobian_ex_pose;

2.IMU：

IMU的真实值为 w,a, 测量值为\(w^{~}, a^{~}\)，则有：



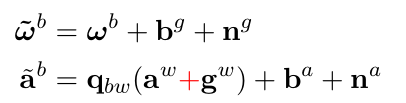
其中： b为bias随机游走误差，n为白噪声。

预积分：

预积分仅仅与imu测量值有关，将一段时间的imu数据直接积分起来就得到了与积分量

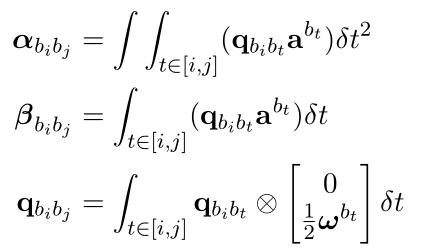
则j时刻的PVQ积分积分方程为：



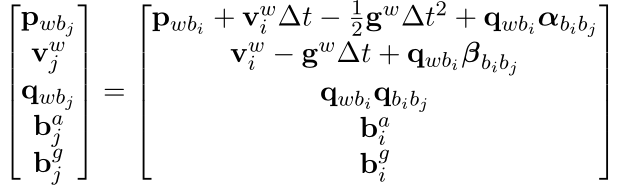
其中p为位移，v为速度，q为姿态，b为bias噪声

2.1 IMU的与积分误差：

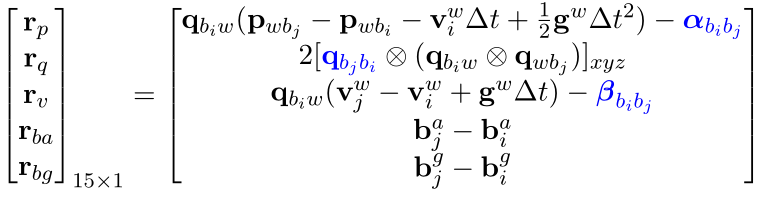
其中，位移，速度，bias噪声的误差都是直接相减，第二项是关于四元数的旋转误差，后缀xyz代表取四元数的虚部（x, y, z）组成的三维向量。

void EdgeImu::ComputeResidual() {
    VecX param_0 = verticies_[0]->Parameters();
    Qd qi(param_0[6], param_0[3], param_0[4], param_0[5]);
    Vec3 pi = param_0.head<3>();
    SO3d ri(qi);
    SO3d ri_inv = ri.inverse();

    VecX param_1 = verticies_[1]->Parameters();
    Vec3 vi = param_1.head<3>();
    Vec3 bai = param_1.segment(3, 3);
    Vec3 bgi = param_1.tail<3>();

    VecX param_2 = verticies_[2]->Parameters();
    Qd qj(param_2[6], param_2[3], param_2[4], param_2[5]);
    Vec3 pj = param_2.head<3>();

    VecX param_3 = verticies_[3]->Parameters();
    Vec3 vj = param_3.head<3>();
    Vec3 baj = param_3.segment(3, 3);
    Vec3 bgj = param_3.tail<3>();
    SO3d rj(qj);

    double dt = pre_integration_->GetSumDt();
    double dt2 = dt * dt;
    SO3d dr;
    Vec3 dv;
    Vec3 dp;
    pre_integration_->GetDeltaRVP(dr, dv, dp);  //获取预积分值

    SO3d res_r = dr.inverse() * ri_inv * rj;
    residual_.block<3, 1>(0, 0) = SO3d::log(res_r);
    residual_.block<3, 1>(3, 0) = ri_inv * (vj - vi - gravity_ * dt) - dv;
    residual_.block<3, 1>(6, 0) = ri_inv * (pj - pi - vi * dt - 0.5 * gravity_ * dt2) - dp;
    residual_.block<3, 1>(9, 0) = baj - bai;
    residual_.block<3, 1>(12, 0) = bgj - bgi;
}

2.2 IMU的误差雅可比矩阵：

基于泰勒展开的误差传递(EKF):

非线性系统\(x_{k} = f(x_{k-1}, u_{k-1})\) 的状态误差的线性递推关系为：



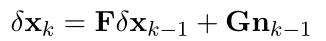
其中，F是状态量\(x_{k}\)对状态量\(x_{k-1}\)的雅可比矩阵，G是状态量\(x_{k}对输入量\)u_{k-1}$的雅可比矩阵。

IMU的误差传递方程为：





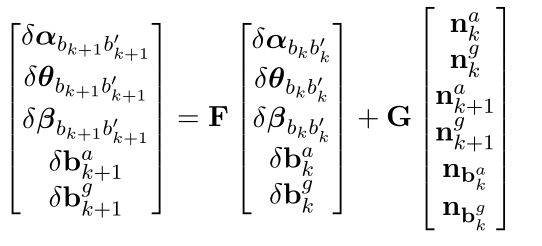
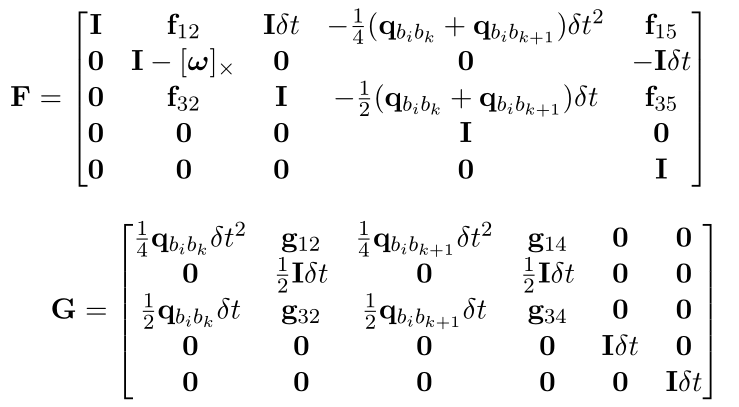
其中的系数为：

• 速度预积分对各状态量的雅可比，为F的第三行，分别是：位移预积分，旋转预积分，速度预积分，陀螺仪bias噪声，加速度bias噪声
  
  f33： 速度预积分量对上一时刻速度预积分量的雅可比，为I
  
  f32： 速度预积分量对角度预积分量的雅可比
  
  f35： 速度预积分量对k时刻角速度bias噪声的雅可比
  
  f22： 前一时刻的旋转误差如何影响当前旋转误差

2.3 IMU相对于优化变量的雅可比矩阵：

在求解非线性方程式，我们需要知道IMU误差对两个关键帧i,j的状态p,q,v,\(b^{a}, b^{g}\)的雅可比

• 对i时刻的位移：
• 对i时刻的旋转：
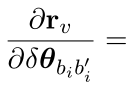
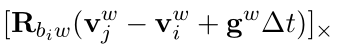
• 对i时刻的速度：
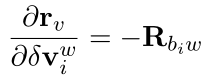
• 对i时刻的加速度bias:
  
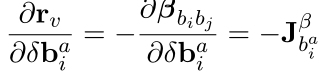
  IMU角度误差相对于优化变量的雅可比
• 角度误差对i时刻的姿态求导：
  
  
  
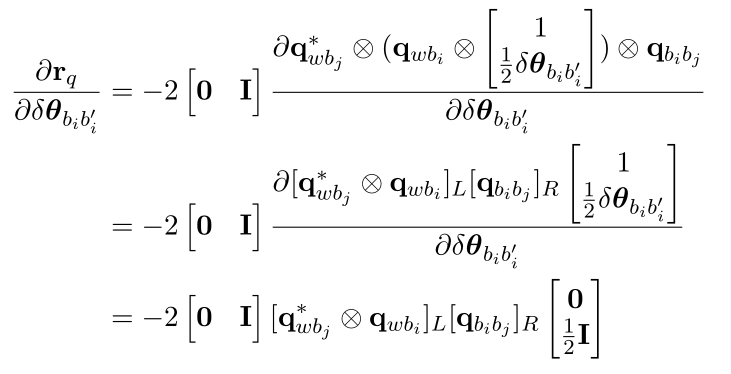
  其中[]L 和[]R 为四元数转为左/右旋转矩阵的算子
• 角度误差对j时刻姿态求导
  
  
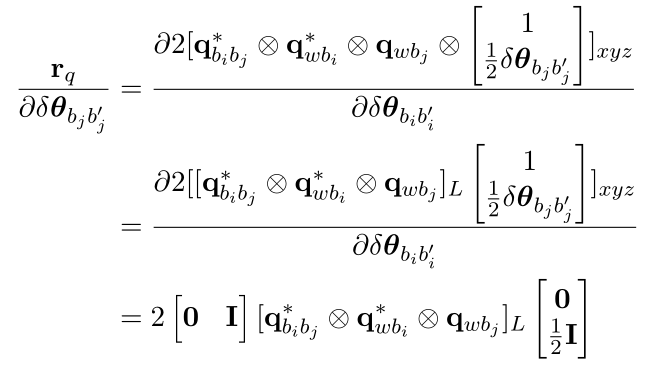
• 角度误差对i时刻陀螺仪bias噪声求导
  
  

void EdgeImu::ComputeJacobians() {

    VecX param_0 = verticies_[0]->Parameters();
    Qd Qi(param_0[6], param_0[3], param_0[4], param_0[5]);
    Vec3 Pi = param_0.head<3>();

    VecX param_1 = verticies_[1]->Parameters();
    Vec3 Vi = param_1.head<3>();
    Vec3 Bai = param_1.segment(3, 3);
    Vec3 Bgi = param_1.tail<3>();

    VecX param_2 = verticies_[2]->Parameters();
    Qd Qj(param_2[6], param_2[3], param_2[4], param_2[5]);
    Vec3 Pj = param_2.head<3>();

    VecX param_3 = verticies_[3]->Parameters();
    Vec3 Vj = param_3.head<3>();
    Vec3 Baj = param_3.segment(3, 3);
    Vec3 Bgj = param_3.tail<3>();

    double sum_dt = pre_integration_->sum_dt;
    Eigen::Matrix3d dp_dba = pre_integration_->jacobian.template block<3, 3>(O_P, O_BA);
    Eigen::Matrix3d dp_dbg = pre_integration_->jacobian.template block<3, 3>(O_P, O_BG);

    Eigen::Matrix3d dq_dbg = pre_integration_->jacobian.template block<3, 3>(O_R, O_BG);

    Eigen::Matrix3d dv_dba = pre_integration_->jacobian.template block<3, 3>(O_V, O_BA);
    Eigen::Matrix3d dv_dbg = pre_integration_->jacobian.template block<3, 3>(O_V, O_BG);

    if (pre_integration_->jacobian.maxCoeff() > 1e8 || pre_integration_->jacobian.minCoeff() < -1e8)
    {
        // ROS_WARN("numerical unstable in preintegration");
    }

//    if (jacobians[0])
    {
        Eigen::Matrix<double, 15, 6, Eigen::RowMajor> jacobian_pose_i;
        jacobian_pose_i.setZero();

        jacobian_pose_i.block<3, 3>(O_P, O_P) = -Qi.inverse().toRotationMatrix();
        jacobian_pose_i.block<3, 3>(O_P, O_R) = Utility::skewSymmetric(Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt));

        Eigen::Quaterniond corrected_delta_q = pre_integration_->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration_->linearized_bg));
        jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Utility::Qleft(Qj.inverse() * Qi) * Utility::Qright(corrected_delta_q)).bottomRightCorner<3, 3>();
        jacobian_pose_i.block<3, 3>(O_V, O_R) = Utility::skewSymmetric(Qi.inverse() * (G * sum_dt + Vj - Vi));

        if (jacobian_pose_i.maxCoeff() > 1e8 || jacobian_pose_i.minCoeff() < -1e8)
        {
        //     ROS_WARN("numerical unstable in preintegration");
        }
        jacobians_[0] = jacobian_pose_i;
    }
//    if (jacobians[1])
    {
        Eigen::Matrix<double, 15, 9, Eigen::RowMajor> jacobian_speedbias_i;
        jacobian_speedbias_i.setZero();
        jacobian_speedbias_i.block<3, 3>(O_P, O_V - O_V) = -Qi.inverse().toRotationMatrix() * sum_dt;
        jacobian_speedbias_i.block<3, 3>(O_P, O_BA - O_V) = -dp_dba;
        jacobian_speedbias_i.block<3, 3>(O_P, O_BG - O_V) = -dp_dbg;

        jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * pre_integration_->delta_q).bottomRightCorner<3, 3>() * dq_dbg;

        jacobian_speedbias_i.block<3, 3>(O_V, O_V - O_V) = -Qi.inverse().toRotationMatrix();
        jacobian_speedbias_i.block<3, 3>(O_V, O_BA - O_V) = -dv_dba;
        jacobian_speedbias_i.block<3, 3>(O_V, O_BG - O_V) = -dv_dbg;

        jacobian_speedbias_i.block<3, 3>(O_BA, O_BA - O_V) = -Eigen::Matrix3d::Identity();

        jacobian_speedbias_i.block<3, 3>(O_BG, O_BG - O_V) = -Eigen::Matrix3d::Identity();

        jacobians_[1] = jacobian_speedbias_i;
    }
//    if (jacobians[2])
    {
        Eigen::Matrix<double, 15, 6, Eigen::RowMajor> jacobian_pose_j;
        jacobian_pose_j.setZero();

        jacobian_pose_j.block<3, 3>(O_P, O_P) = Qi.inverse().toRotationMatrix();
        Eigen::Quaterniond corrected_delta_q = pre_integration_->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration_->linearized_bg));
        jacobian_pose_j.block<3, 3>(O_R, O_R) = Utility::Qleft(corrected_delta_q.inverse() * Qi.inverse() * Qj).bottomRightCorner<3, 3>();

        jacobians_[2] = jacobian_pose_j;

    }
//    if (jacobians[3])
    {
        Eigen::Matrix<double, 15, 9, Eigen::RowMajor> jacobian_speedbias_j;
        jacobian_speedbias_j.setZero();

        jacobian_speedbias_j.block<3, 3>(O_V, O_V - O_V) = Qi.inverse().toRotationMatrix();

        jacobian_speedbias_j.block<3, 3>(O_BA, O_BA - O_V) = Eigen::Matrix3d::Identity();

        jacobian_speedbias_j.block<3, 3>(O_BG, O_BG - O_V) = Eigen::Matrix3d::Identity();

        jacobians_[3] = jacobian_speedbias_j;

    }

}