随机分布和随机数生成—

在人们的生活中，很多场景都需要用到随机数，例如福利彩票，车牌摇号，公共用房分配等。在用数学模型，包括概率统计模型处理实际应用中的问题时，我们希望建立的模型能够尽可能地符合实际情况。但是，实际情况是错综复杂的，如果一味地要求模型与实际完全相符，会导致模型过于复杂，以至于不能进行严格理论分析。所以实际建模时会忽略许多细节，为使得模型比较简单，引入随机数对许多理论进行分析研究。

一、概率密度函数与概率分布函数

概率密度函数用来描述连续型数据的概率，即描述随机变量在某一确定取值点的可能性的函数，用$f(x)$表示，$f(x)$在特定区间的积分值称为变量$x$属于该区间的概率密度函数，记分布函数

\[F(x)={\int}^{x}_{-\infty}{f(x)dx}
\]

概率分布函数$F(x)$可用来描述离散型数据的概率。后面也用$p(x)$描述随机变量在某一确定取值点的可能性的函数，即$p(x)$是离散随机变量在特定取值上的概率，如$p(1)、p(0)$。

分位数是分布函数的逆（反）函数，即给定概率值计算出的随机变量的取值。在参数估计和假设检验中常常用到。

概率分布函数和概率密度函数，无非是用来描述事件在某个点或者某个区间内发生的概率大小。将其分为概率分布和概率密度函数，实质上是对连续性变量和离散型变量的分类讨论，特定数值，特定分析。概率分布函数和概率密度函数的全区间的结果必都为1，即事件在全区间段内必会发生。

二、随机分布

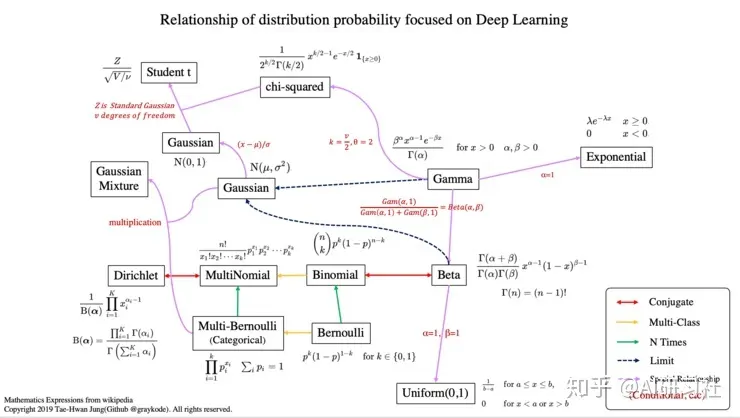
概率分布相关函数汇总参看下图

三、随机数生成

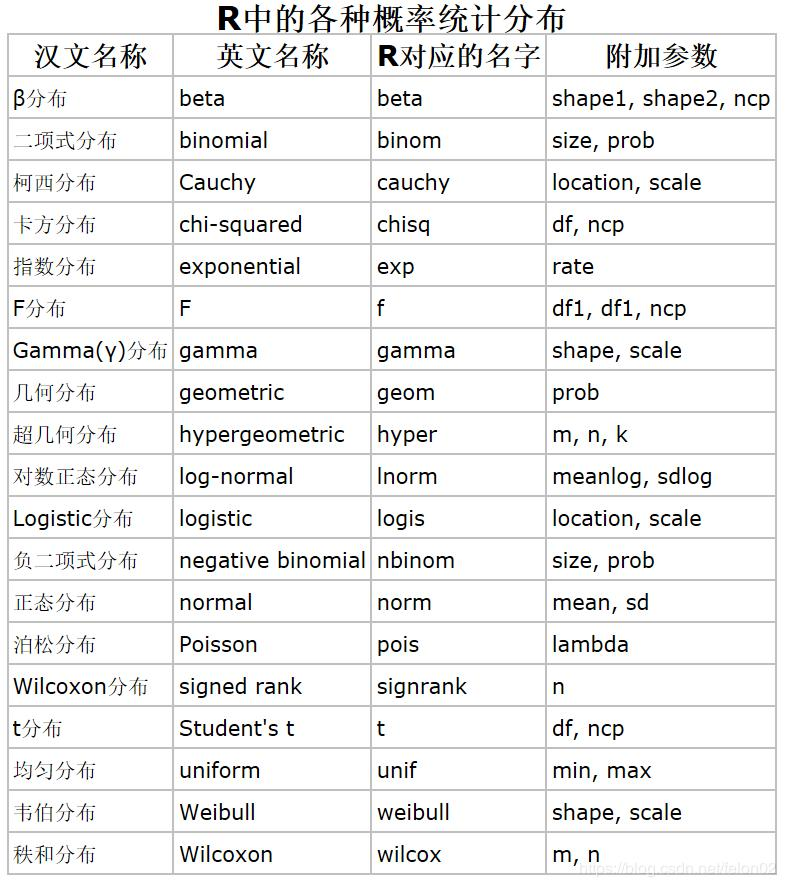
在R中各种概率函数都有统一的形式，即一套统一的前缀+分布函数名：

d 表示密度函数（density）；

p 表示分布函数（生成相应分布的累积概率密度函数）；

q 表示分位数函数，能够返回特定分布的分位数（quantile）；

r 表示随机函数，生成特定分布的随机数（random）

分布	随机数	概率密度	分布函数	分位数函数
正态分布	rnorm	dnorm	pnorm	qnorm
二项分布	rbinom	dbinom	pbinom	qbinom
负二项分布	rnbinom	dnbinom	pnbinom	qnbinom
几何分布	rgeom	dgeom	pgeom	qgeom
超几何分布	rhyper	dhyper	phyper	qhyper
F分布	rf	df	pf	qf
泊松分布	rpois	dpois	ppois	qpois
t分布	rt	dt	pt	qt
连续均匀分布	runif	dunif	punif	qunif

以二项分布为例，实现上述各类函数

dbinom(x, size, prob, log = FALSE)# 可用于计算二项分布的概率。

pbinom(q, size, prob, lower.tail = TRUE, log.p = FALSE)#二项分布的分布函数值

qbinom(p, size, prob, lower.tail = TRUE, log.p = FALSE)#生成二项分布的特定分位数

rbinom(n, size, prob)#生成二项分布的随机数

3.1 rbinom()

rbinom(n, size, prob) 是生成二项分布随机数的函数：n表示生成的随机数数量，size表示进行贝努力试验的次数，prob表示一次贝努力试验成功的概率。

二项分布是指n次独立重复贝努力试验成功的次数的分布，每次贝努力试验的结果只有两个，成功和失败，记成功的概率为p

rbinom(50, size =1, prob = 0.7)

 [1] 1 0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 0 1

[32] 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1

3.2 rnorm（）

正态分布随机数的生成函数是 rnorm（n,mean=0,sd=1）: n表示生成的随机数数量，mean是正态分布的均值，默认为0，sd是正态分布的标准差，默认时为1。

rnorm(100, mean = 0, sd = 1)

 [1]  0.76783  1.09322  0.33601 -0.98324 -0.44368 -0.53098 -0.40858  2.01895 -0.97241

 [10] -1.31241 -0.01927 -1.24650 -0.97130  0.15141  0.38303 -1.02315  1.13883  0.59859

 [19]  0.00686  0.28861  1.36133  0.50797 -1.67239 -0.40857 -0.36354 -0.07675 -0.99930

 [28]  0.42494  1.04411  0.08761  0.13990  0.28055 -1.35221  0.18436  1.75845  0.51947

 [37]  1.36835 -0.71304 -0.88909  0.82046  1.30747  0.77086 -1.55077 -1.14196  1.25769

 [46] -0.69147  0.04648 -1.08179 -0.62592  1.20181 -1.21098 -0.47295  0.50079 -0.31153

 [55] -0.14242  0.88848  0.87554 -0.61668  0.04143 -0.47707  0.12071 -1.42551 -0.58143

 [64] -0.46594 -1.16403 -0.74396 -0.33789  0.19360  0.70602  0.76989 -0.70990 -0.82788

 [73] -0.34566 -0.93789  0.86371 -0.40835 -0.65136  0.23898 -0.00900 -0.67150 -0.86754

 [82]  0.24687 -0.07485  0.82163 -1.26949 -2.11648 -1.05591  0.30317  0.79894  0.25390

 [91] -0.05534 -0.26624  0.74114 -1.21227 -0.14231  0.93185  1.31570  0.35381 -0.54197

 [100] -2.43955

3.3 sample(）

抽样函数sample（x, size, replace = FALSE, prob = NULL)：x（范围），size（抽样个数），replace有无放回的抽样，prob概率，可实现从随机数中取样，给随机数分组等等。

x<-rnorm(100, mean = 0, sd = 1)

sample(x, 30, replace = TRUE)

[1]   1.3294 -0.2839 -0.6261 -0.4688  0.0343 -0.3838 -0.0318  0.7202  0.4057  0.9090

[11]  0.8505 -1.3871 -0.4807 -0.7399 -0.7399 -1.0414 -0.2077 -1.1316  0.9259  0.5612

[21] -1.0414 -0.4404 -0.0786  0.6309 -0.3348 -0.5885  0.4280 -0.2017  0.2506  0.3028

x<-rnorm(100, mean = 0, sd = 1)

index <- sample(c(1,2),size = length(x),replace=TRUE,prob = c(0.7,0.3))

traindata <- x[index == 1]

testdata  <- x[index == 2]

testdata

[1] -0.320  0.506 -0.469 -0.734  0.464  0.688  0.380 -1.302  0.710 -0.486 -0.537  0.140

[13] -0.115  1.285 -1.511  1.288 -0.458  1.708  0.232  0.644  0.215  0.839 -0.262  0.759

[25] -0.473 -0.535 -1.435  0.396 -0.510 -0.622 -1.788 -0.385 -0.629  1.134 -2.161

四、总结

随机数在密码学中有着非常基础且重要的地位,常用于密钥和安全参数生成。而在日常生活中,随机数也是保障公平性的重要手段,广泛应用于抽样、抽签、抽奖等场景当中。随机数在区块链中也应用广泛,除了密钥生成等传统安全场景,在共识机制、零知识证明等热门场景中也发挥着重要的作用,保护着区块链的安全。

参考文献

1.(生成随机数)[https://www.pianshen.com/article/8267220730/]

2.(R语言-11利用sample函数抽样)[https://www.jianshu.com/p/aa9154786dd2]