Mesokurtic,Leptokurtic, Platykurtic介绍

【原文地址1】

【原文地址2】

简要介绍

这三个东西其实是把峰度（Kurtosis）分成了三种类别，峰度也就是评测一个分布的尾部与正态分布的尾部有多不同的定量测量值（如下图所示）。

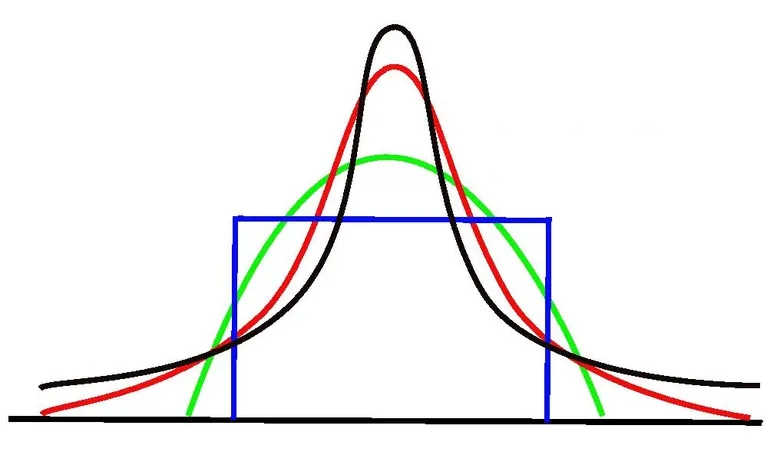
对于一个正态分布的峰度来说，其峰度为3，所以如果一个分布的峰度大于3，也就是其Excess Kurtosis（Excess Kurtosis=Kurtosis - 3）大于0的话，那么就把其称之为Leptokurtic。如果峰度Excess Kurtosis小于0，那么把这个分布称之为Platykurtic，如果基本上等于0，那么把这个分布称之为Mesokurtic，

所以如果Leptokurtic的Excess Kurtosis值不算很大，Platykurtic的Excess Kurtosis值不算很小，这个分布也是可以被称作Mesokurtic的。

下面来直观感受一下三个峰度所对应的分布的形状：

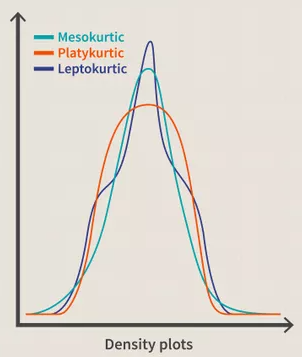
从上图我们可以看出蓝色曲线在如下图所示的地区的概率明显要高，也就是意味着该分布的小概率事件发生的概率会大一点，也许有人会有疑惑：你看两个脚那里不是比其他的要低吗？我的理解是这样的：在两端尾部，概率其实都很低很低，所以这个分布在极低的概率上比其他的分布的概率低，实际上也低不到哪里去。

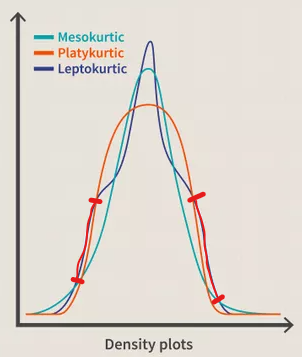
所以对于Platykurtic和Mesokurtic的分布来说，其小概率事件（股票里面的大涨大跌）发成的几率相对较小，所以那些涨幅比较小的股票，其日回报在一年的高度来看的话，其分布是比较接近Mesokurtic和Platykurtic的。