Catalan数（卡特兰数）

Catalan数（卡特兰数）

卡特兰数：规定h(0)＝1，而h(1)＝1，h(2)＝2，h(3)＝5，h(4)＝14，h(5)＝42，h(6)＝132，h(7)＝429，h(8)＝1430，h(9)＝4862，h(10)＝16796，h(11)＝58786，h(12)＝208012，h(13)＝742900，h(14)＝2674440，h(15)＝9694845·····················

原理

令h(0)=1,h(1)=1，catalan数满足递推式  ：

h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)

例如：h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2

h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5

另类递推式[3]  ：

h(n)=h(n-1)*(4*n-2)/(n+1);

递推关系的解为：

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

递推关系的另类解为：

h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)

 

应用

实质上都是递推等式的应用

 

1、一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?

常规分析

首先，我们设f（n）=序列个数为n的出栈序列种数。（我们假定，最后出栈的元素为k，显然，k取不同值时的情况是相互独立的，也就是求出每种k最后出栈的情况数后可用加法原则，由于k最后出栈，因此，在k入栈之前，比k小的值均出栈，此处情况有f(k-1)种，而之后比k大的值入栈，且都在k之前出栈，因此有f(n-k)种方式，由于比k小和比k大的值入栈出栈情况是相互独立的，此处可用乘法原则，f(n-k)*f(k-1)种，求和便是Catalan递归式。）

首次出空之前第一个出栈的序数k将1~n的序列分成两个序列，其中一个是1~k-1，序列个数为k-1，另外一个是k+1~n，序列个数是n-k。

此时，我们若把k视为确定一个序数，那么根据乘法原理，f（n）的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数，即选择k这个序数的f（n）=f（k-1）×f（n-k）。而k可以选1到n，所以再根据加法原理，将k取不同值的序列种数相加，得到的总序列种数为：f（n）=f（0）f（n-1）+f（1）f（n-2）+……+f（n-1）f（0）。

看到此处，再看看卡特兰数的递推式，答案不言而喻，即为f（n）=h（n）= C（2n,n）/（n+1）= c（2n,n）-c（2n,n-1）（n=0，1，2，……）。

最后，令f（0）=1，f（1）=1。

 

非常规分析

对于每一个数来说，必须进栈一次、出栈一次。我们把进栈设为状态‘1’，出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b)，因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数，1的累计数不小于0的累计数的方案种数。

在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求（由左而右扫描，0的累计数大于1的累计数）的方案数即为所求。

不符合要求的数的特征是由左而右扫描时，必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数，此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换，使之成为n-m个0和n-m-1个1，结果得1个由n+1个0和n-1个1组成的2n位数，即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。

反过来，任何一个由n+1个0和n-1个1组成的2n位二进制数，由于0的个数多2个，2n为偶数，故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换，使之成为由n个0和n个1组成的2n位数，即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。

因而不合要求的2n位数与n+1个0，n－1个1组成的排列一一对应。

显然，不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=c(2n,n)/(n+1)=h(n)。

 

2、有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？

  思路：可以将持5元买票视为进栈，那么持10元买票视为5元的出栈。这个问题就转化成了栈的出栈次序数。由应用三的分析直接得到结果，f(2n) 等于h(n)*n!*n!。

 

3、在图书馆一共6个人在排队，3个还《面试宝典》一书，3个在借《面试宝典》一书，图书馆此时没有了面试宝典了，求他们排队的总数？

分析：和上面一题剧院买票时一样的

h(3)=5；所以总数为5*3！*3！=180.

 

4、矩阵连乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？

思路：可以这样考虑，首先通过括号化，将P分成两个部分（就相当于分成了两个子问题），然后分别对两个部分进行括号化。比如分成(a1)×(a2×a3.....×an)，然后再对(a1)和(a2×a3.....×an)分别括号化；又如分成(a1×a2)×(a3.....×an)，然后再对(a1×a2)和(a3.....×an)括号化。

设n个矩阵的括号化方案的种数为f(n)，那么问题的解为

f(n) = f(1)*f(n-1) + f(2)*f(n-2) + f(3)*f(n-3) + f(n-1)*f(1)。f(1)*f(n-1)表示分成(a1)×(a2×a3.....×an)两部分，然后分别括号化。

计算开始几项，f(1) = 1, f(2) = 1, f(3) = 2, f(4) = 5。结合递归式，不难发现f(n)等于h(n-1)。

 

5、n对括号有多少种匹配方式？

思路：n对括号相当于有2n个符号，n个左括号、n个右括号，可以设问题的解为f(2n)。第0个符号肯定为左括号，与之匹配的右括号必须为第2i+1字符。因为如果是第2i个字符，那么第0个字符与第2i个字符间包含奇数个字符，而奇数个字符是无法构成匹配的。

其实可以把问题转化为矩阵连乘，每一个括号里面的内容就看做矩阵连乘的一部分。

 

6、凸多边形三角划分：在一个凸多边形中，通过若干条互不相交的对角线，把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n，求不同划分的方案数f（n）。

思路：以凸多边形的一边为基，设这条边的2个顶点为A和B。从剩余顶点中选1个，可以将凸多边形分成三个部分，中间是一个三角形，左右两边分别是两个凸多边形，然后求解左右两个凸多边形。

设问题的解f(n)，其中n表示顶点数，那么f(n) = f(2)*f(n-1) + f(3)*f(n-2) + ......f(n-2)*f(3) + f(n-1)*f(2)。f(2)*f(n-1)表示三个相邻的顶点构成一个三角形，那么另外两个部分的顶点数分别为2和n-1。

设f(2) = 1，那么f(3) = 1, f(4) = 2, f(5) = 5。结合递推式，不难发现f(n) 等于h(n-2)。

 

 7、一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？

可以看成凸多边形三角划分，它的路线图就相当于一个凸多边形三角划分里面的一种情况。

 

8、在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？

思路：以其中一个点为基点，编号为0，然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定是奇数，否则，这两个编号间含有奇数个点，势必会有个点被孤立，即在一条线段的两侧分别有一个孤立点，从而导致两线段相交。设选中的基点为A，与它连接的点为B，那么A和B将所有点分成两个部分，一部分位于A、B的左边，另一部分位于A、B的右边（详单与把问题划分为左右两个子问题）。然后分别对这两部分求解即可。

设问题的解f(n)，那么f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ......f(n-4)*f(2) + f(n-2)*f(0)。f(0)*f(n-2)表示编号0的点与编号1的点相连，此时位于它们右边的点的个数为0，而位于它们左边的点为2n-2。依次类推。

f(0) = 1, f(2) = 1, f(4) = 2。结合递归式，不难发现f(2n) 等于h(n)。

9、圆桌周围有 2n个人，他们两两握手，但没有交叉的方案数为h(n)

和上一题是一样的，都是圆上，都没有交叉。都是分成左右两个子问题来分析。

10、n*n的方格地图中，从一个角到另外一个角，不跨越对角线的路径数为h(n).

例如， 4×4方格地图中的路径有：

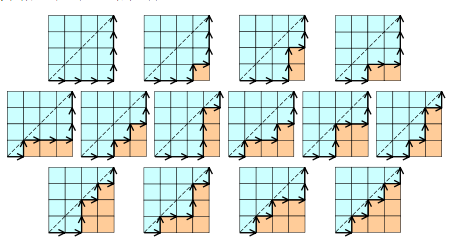
11、n个节点构成的二叉树，共有多少种情形？

和上一题是一样的，上一题是分为左右两个子问题，而这一题是二叉树，分成左孩子和右孩子两个子问题就好了。

思路：可以这样考虑，根肯定会占用一个结点，那么剩余的n-1个结点可以有如下的分配方式，T(0, n-1),T(1, n-2),...T(n-1, 0)，设T(i, j)表示根的左子树含i个结点，右子树含j个结点。

设问题的解为f(n)，那么f(n) = f(0)*f(n-1) + f(1)*f(n-2) + .......+ f(n-2)*f(1) + f(n-1)*f(0)。假设f(0) = 1，那么f(1) = 1, f(2) = 2, f(3) = 5。结合递推式，不难发现f(n)等于h(n)。

12、拥有 n+1 个叶子节点的二叉树的数量为h(n).

例如 4个叶子节点的所有二叉树形态：

参考：

http://buptdtt.blog.51cto.com/2369962/832586

https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0?fr=aladdin