【22.48%】【codeforces 689D】Friends and Subsequences

time limit per test2 seconds

memory limit per test512 megabytes

inputstandard input

outputstandard output

Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?

Every one of them has an integer sequences a and b of length n. Being given a query of the form of pair of integers (l, r), Mike can instantly tell the value of 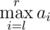while !Mike can instantly tell the value of .

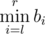Now suppose a robot (you!) asks them all possible different queries of pairs of integers (l, r) (1 ≤ l ≤ r ≤ n) (so he will make exactly n(n + 1) / 2 queries) and counts how many times their answers coincide, thus for how many pairs 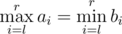is satisfied.

How many occasions will the robot count?

Input

The first line contains only integer n (1 ≤ n ≤ 200 000).

The second line contains n integer numbers a1, a2, …, an ( - 109 ≤ ai ≤ 109) — the sequence a.

The third line contains n integer numbers b1, b2, …, bn ( - 109 ≤ bi ≤ 109) — the sequence b.

Output

Print the only integer number — the number of occasions the robot will count, thus for how many pairs 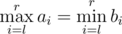is satisfied.

Examples

input

6

1 2 3 2 1 4

6 7 1 2 3 2

output

2

input

3

3 3 3

1 1 1

output

0

Note

The occasions in the first sample case are:

1.l = 4,r = 4 since max{2} = min{2}.

2.l = 4,r = 5 since max{2, 1} = min{2, 3}.

There are no occasions in the second sample case since Mike will answer 3 to any query pair, but !Mike will always answer 1.

【题解】



用ST算法搞(也就是RMQ算法);

这可以搞定任意两个点之间的最大值和最小值。

接着顺序枚举起点i

对于每个起点i，二分枚举它的终点t;

①如果[i..t]这段区间内a的最大值大于b的最小值，则右端点再也不能往右了。因为再往右只会让这个差距越来越大，不能让他们相等。

②如果[i..t]这段区间内a的最大值等于b的最小值,则这是一个可行的右端点。

③如果[i..t]这段区间内a的最大值小于b的最小值,则右端点可以再往右,以逼近max==min(当然也可能不存在);

总之，枚举起点i,然后找到最靠左的满足要求的右端点t1，和最靠右的满足要求的右端点t2,答案对数增加t2-t1+1

这个t1和t2可以用两个二分写出来(分开写)

#include <cstdio>
#include <iostream>
#include <algorithm>

using namespace std;

const int MAX = 18;
const int MAXN = 209999;
const int INF = 2e9;

int dpmax[210000][MAX + 3],dpmin[210000][MAX + 3];
int pre2[MAX + 3];
int a[MAXN], b[MAXN];
int need[MAXN];
int n;

void input(int &r)
{
    r = 0;
    char t = getchar();
    while (!isdigit(t) && t!='-') t = getchar();
    int sign =1;
    if (t == '-') sign = -sign;
    while (!isdigit(t)) t = getchar();
    while (isdigit(t)) r = r * 10 + t - '0', t = getchar();
    r = r*sign;
}

int main()
{
    //freopen("F:\\rush.txt", "r", stdin);
    input(n);
    for (int i = 1; i <= n; i++)
        input(a[i]), dpmax[i][0] = a[i];
    for (int i = 1; i <= n; i++)
        input(b[i]), dpmin[i][0] = b[i];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= 18; j++)
            dpmin[i][j] = INF,dpmax[i][j]=-INF;

    pre2[0] = 1;
    for (int i = 1; i <= 18; i++)
        pre2[i] = pre2[i - 1] << 1;

    need[1] = 0; need[2] = 1;
    int temp = 2;
    for (int i = 3; i <= n; i++)//need[i]表示长度为i是2的多少次方,可以理解为[log2i]
        if (pre2[temp] == i)
            need[i] = need[i - 1] + 1, temp++;
        else
            need[i] = need[i - 1];

    for (int l = 1; pre2[l] <= n; l++)//利用st算法搞出区间最大和最小值
        for (int i = 1;i <= n;i++)
            if (i + pre2[l] - 1 <= n)
                dpmax[i][l] = max(dpmax[i][l - 1], dpmax[i + pre2[l - 1]][l - 1]);

    for (int l = 1; pre2[l] <= n; l++)
        for (int i = 1; i <= n; i++)
            if (i + pre2[l] - 1 <= n)
                dpmin[i][l] = min(dpmin[i][l - 1], dpmin[i + pre2[l - 1]][l - 1]);

    long long ans = 0;
    for (int i = 1; i <= n; i++){
        int l = i, r = n;
        //找最左边的
        int numl = -1;
        while (l <= r){
            int m = (l + r) >> 1;
            int len = need[m-i+1];
            int themax = max(dpmax[i][len], dpmax[m - pre2[len] + 1][len]);
            int themin = min(dpmin[i][len], dpmin[m - pre2[len] + 1][len]);
            if (themax > themin)
                r = m-1;
            else
                if (themax == themin){
                    numl = m;
                    r = m - 1;
                }
                else
                    if (themax < themin)
                        l = m + 1;
        }

        //找最右边的
        int numr = -1;
        l = i, r = n;
        while (l <= r) {
            int m = (l + r) >> 1;
            int len = need[m - i + 1];
            int themax = max(dpmax[i][len], dpmax[m - pre2[len] + 1][len]);
            int themin = min(dpmin[i][len], dpmin[m - pre2[len] + 1][len]);
            if (themax > themin)
                r = m - 1;
            else
                if (themax == themin) {
                    numr = m;
                    l = m + 1;
                }
                else
                    if (themax < themin)
                        l = m + 1;
        }
        if (numl != -1)
            ans += (numr - numl + 1);
    }
    printf("%I64d\n", ans);
    return 0;
}