题解 P3521 【[POI2011]ROT-Tree Rotations】

这道题采用权值线段树合并的解法。

---

首先讲一下解法中出现的两个概念：权值线段树与线段树合并。

所谓权值线段树，可以理解为维护的信息反过来的普通线段树，我个人认为值域线段树这个名字其实要准确一些。

举个例子，我们将序列$1,1,2,3,4,4,4,5,6,6$中的数依次插入，那么插入完成之后的效果图大概是下面这样的：

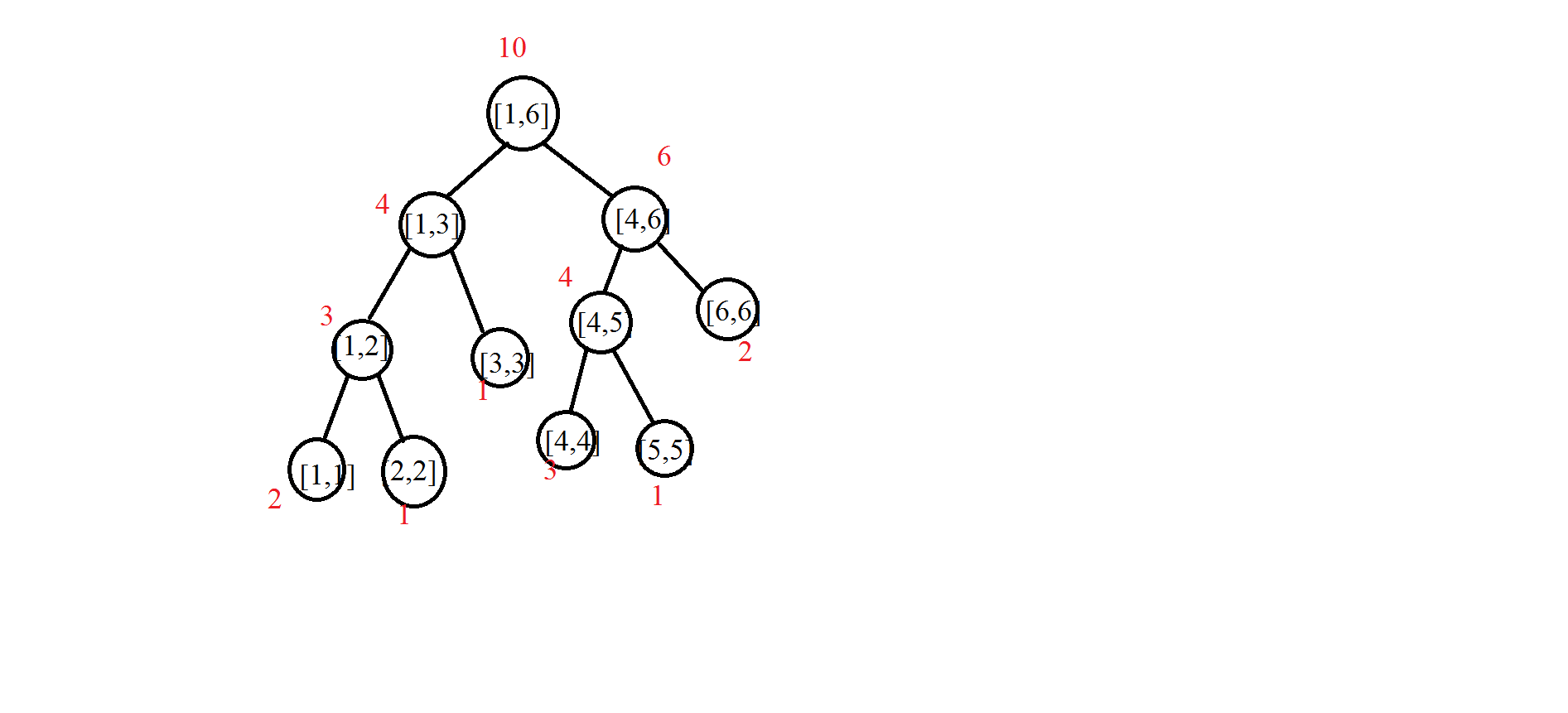
（其中红色为节点的值）

也就是说，每一个节点维护的值是这个区间内的数出现的次数。

在实现权值线段树时，我们通常会采用动态开点的方式，也就是不创建无关的节点，当然也可以离散化数据，否则必然会空间超限。

而线段树合并的原理则是基于线段树较为稳定的结构。

在合并的过程中，我们将两颗线段树对应位置的节点的值合在一起，创建一颗新的线段树。

过程大致如下：

---

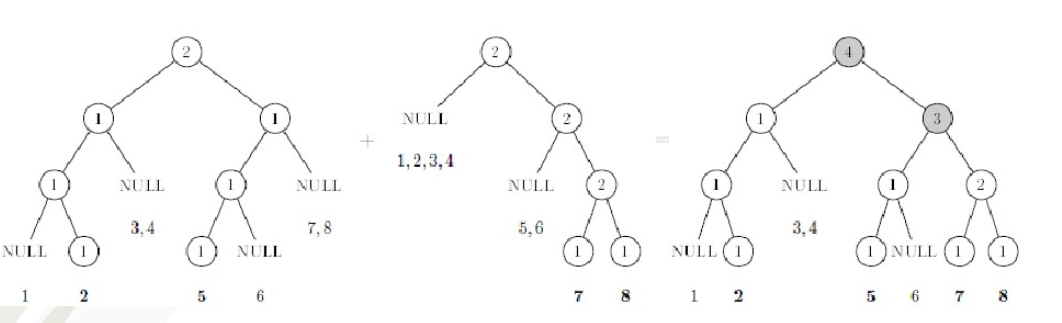
这道题让我们求出逆序对个数最小值，并且允许我们随意交换一个节点的两棵子树。

考虑一个任意的节点，它的子树先序遍历后的逆序对显然只有三种组成：

1. 左子树中

2. 右子树中

3. 跨越左右子树

对子树的交换显然不会影响第1,2类，因此我们只需要计算出第三类的最小值即可。

至于计算则没有什么难度。由于我们维护的是值域，因此左儿子必定比右儿子大，那么我们就用左儿子大小乘以右儿子大小即可得出交换前逆序对个数。交换后同理之。

这里需要注意，我们能够这样计算是因为无论左右儿子怎么交换，影响的都只有当前部分的逆序对个数，而不会影响深度更浅的节点的值。

另：这道题处理输入十分窒息，可参考楼下写法。

---

AC代码如下：

509ms 57236kb

 #include<bits/stdc++.h>

 using namespace std;

 namespace StandardIO {

     template<typename T>inline void read (T &x) {
         x=;T f=;char c=getchar();
         for (; c<''||c>''; c=getchar()) if (c=='-') f=-;
         for (; c>=''&&c<=''; c=getchar()) x=x*+c-'';
         x*=f;
     }

     template<typename T>inline void write (T x) {
         if (x<) putchar('-'),x*=-;
         if (x>=) write(x/);
         putchar(x%+'');
     }

 }

 using namespace StandardIO;

 namespace Solve {

     const int N=;

     int n;
     long long ans,ans1,ans2;
     int tot_node;
     struct node {
         int ls,rs;
         long long val;
     } tree[N*];

     void update (int l,int r,int v,int &pos) {
         if (!pos) pos=++tot_node;
         tree[pos].val++;
         if (l==r) return;
         int mid=(l+r)>>;
         if (v<=mid) update(l,mid,v,tree[pos].ls);
         else update(mid+,r,v,tree[pos].rs);
     }
     void merge (int &x,int y) {
         if (!x||!y) {
             x=x+y;return;
         }
         tree[x].val+=tree[y].val;
         ans1+=(long long)tree[tree[x].rs].val*tree[tree[y].ls].val;
         ans2+=(long long)tree[tree[x].ls].val*tree[tree[y].rs].val;
         merge(tree[x].ls,tree[y].ls);
         merge(tree[x].rs,tree[y].rs);
     }
     void dfs (int &x) {
         int tmp,ls,rs;x=;
         read(tmp);
         if (!tmp) {
             dfs(ls),dfs(rs);
             ans1=ans2=;
             x=ls,merge(x,rs);
             ans+=min(ans1,ans2);
         } else update(,n,tmp,x);
     }

     inline void solve () {
         read(n);
         int tmp=;
         dfs(tmp);
         write(ans);
     }
 }

 using namespace Solve;

 int main () {
 //    freopen(".in","r",stdin);
 //    freopen(".out","w",stdout);
     solve();
 }