matlab-罗曼诺夫斯基准则剔除粗大值
罗曼诺夫斯基准则原理
罗曼诺夫斯基准则又称 t检验准则,其特点是首先删除一个可疑的的测得值,然后按 t分布检验被剔除的测量值是否含有粗大误差
罗曼诺夫斯基准则
1)选取合适的显著度a,选择合适的数据处理长度n。由a、n在t分布表中查出系数K。(例如:a为0.05、n为15,则 K2.24)
2)计算处理段数据的平均值 3)计算处理段数据的标准 4)| 检测值 - 计算处理段数据的平均值 | > K*计算处理段数据的标准差,如果成立则检测值为粗大值,需要剔除。
实现代码
function out = fun_romanovsky(data, l, a)
% 功能:罗曼诺夫斯基准则剔除粗大值
% 参数:
% data 输入数据
% l 分段长度
% a 显著度
% 返回值:剔除粗大值后的数据
[m,n] = size(data);
if m > 1
data = data';
end
if length(data) <= l
out = NaN;
return;
end
out = data;
i1 = 1;
i2 = 1;
while ( i1 <= length(data)-l )
temp = data(i1:i1+l);
data_mean = mean(temp);
% v = temp - data_mean;
% 求方差
temp_std = std(temp);
% K由l、a查表所得
K = 2.24;
if abs(data(i1 + l) - data_mean) > K*temp_std
out(i2 + l) = NaN;
data(i1 + l)= [];
else
i1 = i1 + 1;
end
i2 = i2 + 1;
end
end
测试代码
data = [20.42 20.43 20.40 20.43 20.42 20.43 20.30 20.40 20.43 20.42 20.41 20.39 20.39 20.40 20.40 21.40 20.43 20.39 20.60 20.39 20.42 20.40 20.43];
data1= fun_romanovsky(data, 15, 0.05);
x = 1:length(data);
figure(2);
plot(x, data, 'b-', x , data1, 'ro');
legend('处理前','处理后');
效果图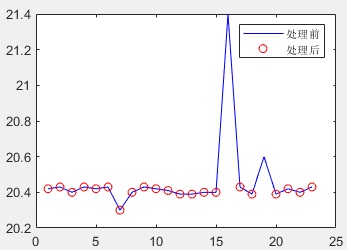
matlab-罗曼诺夫斯基准则剔除粗大值的更多相关文章
- 【Matlab编程】哈夫曼编码的Matlab实现
在前年暑假的时候,用C实现了哈夫曼编译码的功能,见文章<哈夫曼树及编译码>.不过在通信仿真中,经常要使用到Matlab编程,所以为了方便起见,这里用Matlab实现的哈夫曼编码的功能.至于 ...
- 柯尔莫可洛夫-斯米洛夫检验(Kolmogorov–Smirnov test,K-S test)
柯尔莫哥洛夫-斯米尔诺夫检验(Колмогоров-Смирнов检验)基于累计分布函数,用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同. 在进行cumulative probab ...
- MATLAB 大数据剔除坏值
在用MATLAB进行数据分析的时候,坏点对正确结果的影响比较大, 因此,我么需要剔除野点,对于坏值的剔除,我们 利用 3σ准则 剔除无效数据: 3σ准则又称为拉依达准则,它是先假设一组检测数据只含有 ...
- 赫夫曼\哈夫曼\霍夫曼编码 (Huffman Tree)
哈夫曼树 给定n个权值作为n的叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree).哈夫曼树是带权路径长度最短的树,权值较大的结点离 ...
- 切诺夫界证明(Chernoff bound)
- Tikhonov regularization 吉洪诺夫 正则化
这个知识点很重要,但是,我不懂. 第一个问题:为什么要做正则化? In mathematics, statistics, and computer science, particularly in t ...
- x的奇幻之旅 (史蒂夫·斯托加茨 著)
第1部分 数字 第1章 数学:从企鹅的"鱼"订单到无穷大 (已看) 第2章 一组组石头与加减乘除运算 (已看) 第3章 "敌人的敌人就是朋友“与"负负得正&qu ...
- 诺塔斯读写卡QT SDK笔记
卡片操作函数调用 寻卡: Request --> LotusCardRequest 防撞处理: Anticollission --> LotusCardAnticoll 选卡: Selec ...
- matlab中如何根据t检验参数查找t检验值
这个问题花了一些时间.先看图 这个是t检验里面的公式,但是如何在matlab中找到该式子对应的值,我现在才知道. 就是这样:x=tinv(1-α/2,n-1)----t(n)分布的上侧α分位数 ...
随机推荐
- tensorflow报错 tensorflow Resource exhausted: OOM when allocating tensor with shape
在使用tensorflow的object detection时,出现以下报错 tensorflow Resource exhausted: OOM when allocating tensor wit ...
- Android(java)学习笔记4:线程的控制
1. 线程休眠: Java中线程休眠指让正在运行的线程暂停执行一段时间,进入阻塞状态,通过调用Thread类的静态方法sleep得以实现. 当线程调用sleep进入阻塞状态后,在其休眠的时间内,该线程 ...
- Android(java)学习笔记14:Java线程池
1. 线程池: 1)程序启动一个新线程成本是比较高的,因为它涉及到要与操作系统进行交互.而使用线程池可以很好的提高性能,尤其是当程序中要创建大量生存期很短的线程时,更应该考虑使用线程池. 2)线程池里 ...
- Ubuntu 入门安装
写在前面的话:很少一次上这么多干货,主要是对Linux的一些基本操作,常用的软件的安装,这个其实不算什么吧,方便大家也方便我,新手们早点入门Linux,少走弯路,网上资料很多,相当于一个整合咯,都是一 ...
- XCode插件因为升级不能用了怎么办?几个步骤教你搞定
之前XCode安装了自动注释的插件 VVDomenter.升级之后不能使用了怎么办?跟着我做吧. 1.打开xcode插件所在的目录:~/library/Application Support/Deve ...
- Hibernate注解开发示例
-------------------------------------------------------------------customer------------------------- ...
- MySQL优化 ----开篇
今天,数据库的操作越来越成为整个应用的性能瓶颈,Mysql优化则是一个经常要谈的问题了. 谈起MySQL优化,咱们先简单谈一下Mysql: Mysql是最流行的关系型数据库管理系统,在WEB应用方面M ...
- oracle 基础知识(四)常用函数
SQL中的单记录函数 .ASCII 返回与指定的字符对应的十进制数; SQL') zero,ascii(' ') space from dual; A A ZERO SPACE --------- - ...
- Android学习笔记_29_样式和主题
一.简单样式定义和使用: android中的样式和CSS样式作用相似,都是用于为界面元素定义显示风格,它是一个包含一个或者多个view控件属性的集合.如:需要定义字体的颜色和大小. 在Android中 ...
- Tomcat 启动速度优化
创建一个web项目 选择发布到 汤姆猫 的下面 deploy path: 表示发布到的文件名称 把项目添加到 tomcat 里,运行,我们可以在 tomcat里找到我们发布的项目: 现在启动时间: 现 ...
