机器学习之支持向量机（二）：SMO算法

注：关于支持向量机系列文章是借鉴大神的神作，加以自己的理解写成的；若对原作者有损请告知，我会及时处理。转载请标明来源。

序：

我在支持向量机系列中主要讲支持向量机的公式推导，第一部分讲到推出拉格朗日对偶函数的对偶因子α；第二部分是SMO算法对于对偶因子的求解；第三部分是核函数的原理与应用，讲核函数的推理及常用的核函数有哪些；第四部分是支持向量机的应用，按照机器学习实战的代码详细解读。

机器学习之支持向量机（一）：支持向量机的公式推导

机器学习之支持向量机（二）：SMO算法

机器学习之支持向量机（三）：核函数和KKT条件的理解

机器学习之支持向量机（四）：支持向量机的Python语言实现

1 SMO算法的概念

这里补充一点，后面的K () 函数是核函数，是把低维度的数据投射到高维度中，即把非线性转换成线性分类。知道k 是核函数就可以了，后面会再详细讲解k 函数。我们在上篇中得到关于对偶因子的式子，对其求 α 极大，现在添加符号转化成求极小，两者等价。

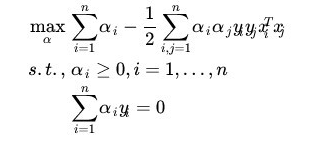
转化后的目标函数：

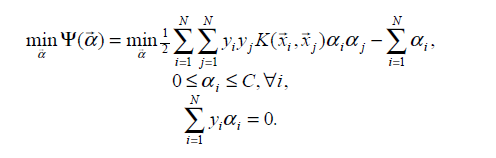
其中 约束条件中 C 是惩罚系数，由对非线性加上松弛因子得到的。

1998年，由Platt提出的序列最小最优化算法(SMO)可以高效的求解上述SVM问题，它把原始求解N个参数二次规划问题分解成很多个子二次规划问题分别求解，每个子问题只需要求解2个参数，方法类似于坐标上升，节省时间成本和降低了内存需求。每次启发式选择两个变量进行优化，不断循环，直到达到函数最优值。

2 SMO算法原理分析

我们的目标：求解对偶因子 α （α₁, α₂, ... , α_N）

2.1 目标函数化成二元函数

SMO算法是通过一定的规定选择两个参数进行优化，并固定其余 N - 2 个参数，假如选取优化的参数是 α₁, α_{2 ，}固定α₃, α₄ , .., α_N ，对目标函数进行化简成二元函数得：

  

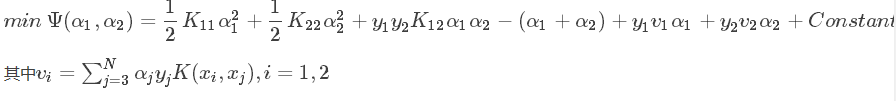
这里强调一下，式子中的 K_ij 是核函数，知道意思就可以，不了解不太影响SMO算法的推导。

2.2 将二元函数化成一元函数

约束条件：

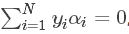    得到 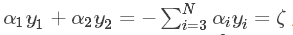    ，其中 ζ 是一个定值。

让两边同时乘以y₁ ,化简得到：

 

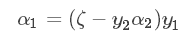
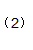
将（2）式带入到（1）中可得：

              

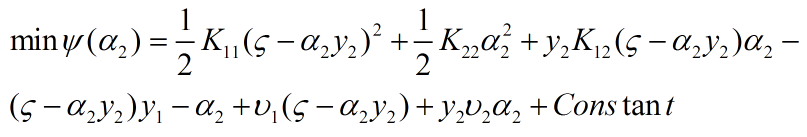
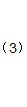
2.3 对一元函数求极值点

对（3）式求导并等于0，得：

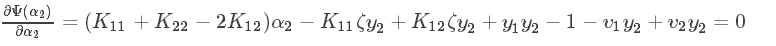
假设求解得到的值，记为α₁^new 、α₂^new 优化前的解记为α₁^old 、α₂^old ，由约束条件知：

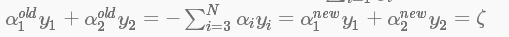   得到：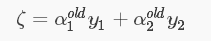       

再设支持向量机超平面模型为：f (x) = ω^Tx + b ,  ω = Σ α_i y_i x_i  即 f (x_i) 为样本x_i 的预测值，y_i 表示 x_i 的真实值，则令E_i 表示误差值。

      

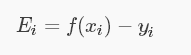
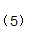
由于 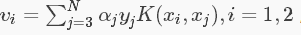  可得：

     

     

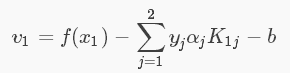
将上面的式子（4）（6）（7）带入求导公式中，此时解出的 α₂^new  没有考虑到约束条件，先记为 α₂^{new unclipped}  ，得：

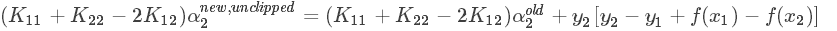
带入（5）式子，得：

   

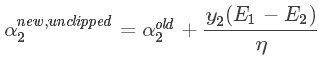
2.4 求得最终的对偶因子

以上求得的 α₂^{new unclipped} 没考虑约束条件：

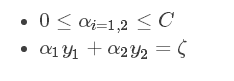
当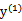和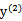异号时，也就是一个为1，一个为-1时，他们可以表示成一条直线，斜率为1。

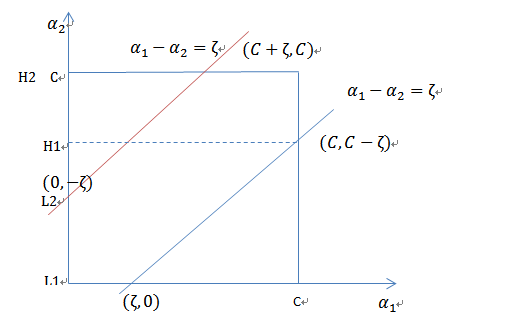
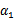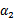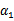横轴是，纵轴是，和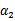既要在矩形方框内，也要在直线上，因此 L  <= α₂^new   <= H

最终得到的值：

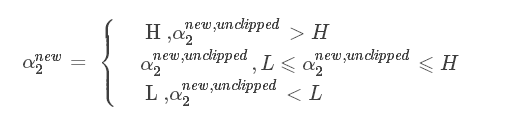
再根据 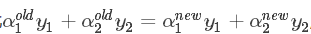 得到 α₁^new ：

   

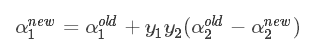
2.5 临界情况的求值

对于大部分情况 η = K₁₁ + K₂₂ - 2K₁₂ > 0 ,求解方式如上；但 η <= 0 , α₂^new 取临界点L或H。

当η<0时，目标函数为凸函数，没有极小值，极值在定义域边界处取得。 
当η=0时，目标函数为单调函数，同样在边界处取极值。

计算方法：

3 启发式选取变量

3.1 对第一个变量的选取

第一个变量的选择称为外循环，首先遍历整个样本集，选择违反KKT条件的αi作为第一个变量，接着依据相关规则选择第二个变量(见下面分析),对这两个变量采用上述方法进行优化。当遍历完整个样本集后，遍历非边界样本集(0<αi<C)中违反KKT的αi作为第一个变量，同样依据相关规则选择第二个变量，对此两个变量进行优化。当遍历完非边界样本集后，再次回到遍历整个样本集中寻找，即在整个样本集与非边界样本集上来回切换，寻找违反KKT条件的αi作为第一个变量。直到遍历整个样本集后，没有违反KKT条件α_i，然后退出。

3.2 对第二个变量的选取

SMO称第二个变量的选择过程为内循环，假设在外循环中找个第一个变量记为α₁，第二个变量的选择希望能使α2有较大的变化，由于α₂是依赖于|E₁−E₂|,当E1为正时，那么选择最小的E_i作为E₂,如果E₁为负，选择最大E_i作为E₂，通常为每个样本的E_i保存在一个列表中，选择最大的|E₁−E₂|来近似最大化步长。

4 阈值b的计算

每完成两个变量的优化后，都要对阈值 b 进行更新，因为关系到 f(x) 的计算，即关系到下次优化时计算。

这部分结束了，通过SMO算法解出的对偶因子的值，可以得到最优的超平面方程 f (x) = ω_Tx + b ，即对样本能够划分。以上大多借鉴了勿在浮沙筑高台的blog 文章，他写的已经很清晰，我只是在他的基础上

增加或删去不好理解的内容。下篇是对核函数和KKT条件的解释。

机器学习之支持向量机（一）：支持向量机的公式推导

机器学习之支持向量机（二）：SMO算法

机器学习之支持向量机（三）：核函数和KKT条件的理解

机器学习之支持向量机（四）：支持向量机的Python语言实现

参考：

1 【机器学习详解】SMO算法剖析  http://blog.csdn.net/luoshixian099/article/details/51227754

2  支持向量机（五）SMO算法

3 支持向量机通俗导论（理解SVM的三层境界）