Cs231n课堂内容记录-Lecture2-Part2 线性分类

Lecture 3

课程内容记录：（上）https://zhuanlan.zhihu.com/p/20918580?refer=intelligentunit

（中）https://zhuanlan.zhihu.com/p/20945670?refer=intelligentunit

（下）https://zhuanlan.zhihu.com/p/21102293?refer=intelligentunit

1．线性分类器（linear classifer）：

我们总是希望得到一个函数f(x,w)，即评分函数（score function），x代表输入数据，往往是图像的numpy矩阵，w是权重或者一些参数，而整个函数的结果对应预测值的一维Numpy矩阵，矩阵中数值最大的预测值代表概率最高的预测对象。我们可以去利用充分地想象力改变f，已得到尽可能高效准确的预测结果，最简单的f就是乘积的形式，也就是线性分类器。

通常我们会添加一个偏置项，他是对应预测结果数的一维向量，它对预测得到的数据进行偏置，以获得更具有取向性的结果（如果你的分类结果中猫的数量大于狗，而测试集中猫狗的数量一致，很可能你的偏置更倾向于猫）。

2．NN和线性分类器的区别：

NN的训练过程只是将训练集图片及标签提取出来，预测过程中找到与预测对象L1距离最小的训练集图像，它对应的标签类别就是预测类别。KNN多了一步是找到K个最小图像进行二次投票。

线性分类器需要得到权重值W和偏置值b，然后相当于利用测试图像去匹配不同类别对应的（W,b）组成的模板图像，最为匹配的则属于该类别。这样极大地节省了测试集测试所需的时间。这时我们所要做的“匹配”过程，是使预测图像得到的评分结果尽可能与训练集中图像的真实类别一致，即评分函数在正确的分类位置应当得到最高的评分。（也就是说通过W，b划分出分类的特定空间）

3．关于支持向量机（SVM：Support Vector Machine）:

支持向量机的基本模型是在特征空间上找到最佳的分离超平面使得训练集上正负样本间隔最大，原用来解决二分类问题的有监督学习算法，在引入了核方法之后SVM也可以用来解决非线性问题。离分离超平面最近的两个数据点被称为支持向量（Support Vector）。

参见吴恩达机器学习课程以及李航《统计学习方法》

4．关于正则化（regularization）:

通过在损失函数中加入后一项，正则化项，我们对W的值进行了制约，希望模型选择更简单的W值。这里的“简单”具体取决于你的模型种类和任务的规模。它同样体现了奥卡姆剃刀的观点：如果你找到了多个可以解释结果的假设，一般来说我们应该选择最简约的假设。因为这样的假设鲁棒性更好，更适用于全新的测试集。基于这一思想，我们希望W的值尽量小。这样我们的损失函数就具有两个项，数据丢失项（data loss）和正则化项（Regularization）。这里我们用到了一种超参数λ用以平衡这两项，称为正则化参数。

关于正则化参数部分，可以参见吴恩达课程。

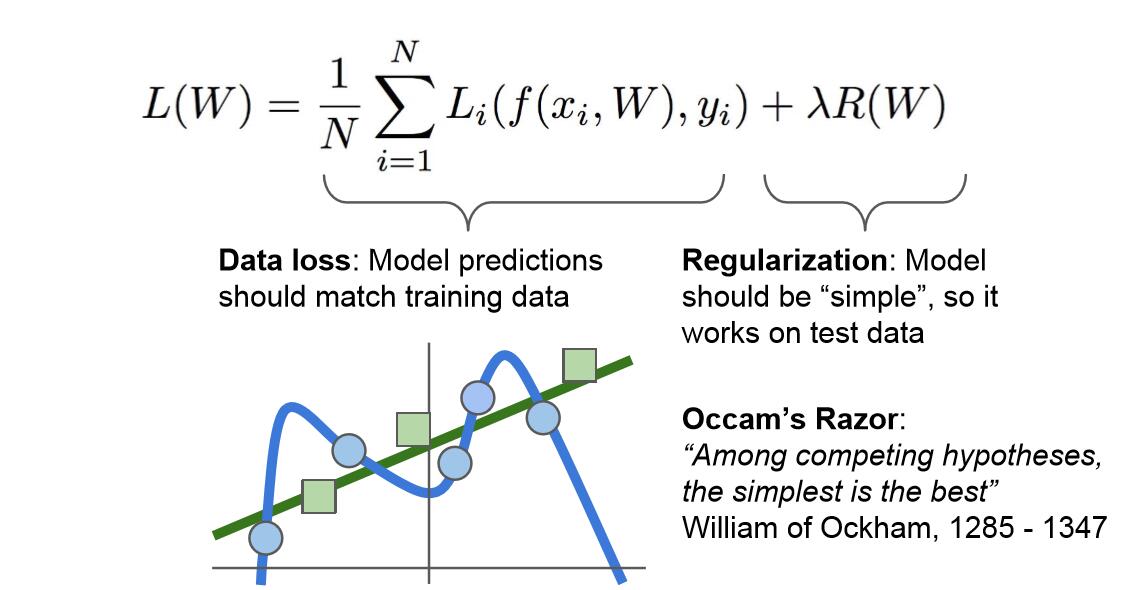
一些正则化方法如下图：

对模型进行正则化（regulairzation），也就是在损失函数中加入正则项的主要目的是为了减轻模型的复杂度，在一定程度上减缓过拟合的速度。

5．关于范数（norm）:

参见：https://blog.csdn.net/a493823882/article/details/80569888

6．支持向量机（SVM）和Softmax分类器的对比:

SVM和Softmax是最常用的两个分类器，Softmax的损失函数和SVM不同，SVM输出f(x,W)，我们得到每个分类的对应的评分大小。而Softmax的输出更加直观，是各分类归一化后的分类概率。在Softmax分类器中，函数f(x，W)=Wx的形式保持不变，但分类器将这些评分值视为每个分类的未归一化的对数概率，并且将折叶损失（hinge loss）替换成了交叉熵损失（cross-entropy loss）。

关于交叉熵的解释以及两者区别的具体例子，以及关于两者区别的一些解释，课程笔记中讲得很好。

注：

关于softmax对数取负的原因：我们将对数概率指数化，归一化之后再取对数，这时如果结果越好当然概率越高，但我们期望loss应该越低才对，所以对结果取负。

Softmax Classifier，又称Multinomial Logistic Regression，多项式逻辑回归。

7．loss function总结：