「AHOI / HNOI2017」单旋

「AHOI / HNOI2017」单旋

题目链接

H 国是一个热爱写代码的国家，那里的人们很小去学校学习写各种各样的数据结构。伸展树（splay）是一种数据结构，因为代码好写，功能多，效率高，掌握这种数据结构成为了 H 国的必修技能。有一天，邪恶的「卡」带着他的邪恶的「常数」来企图毁灭 H 国。「卡」给 H 国的人洗脑说，splay 如果写成单旋的，将会更快。「卡」称「单旋 splay」为「spaly」。虽说他说的很没道理，但还是有 H 国的人相信了，小 H 就是其中之一，spaly 马上成为他的信仰。 而 H 国的国王，自然不允许这样的风气蔓延，国王构造了一组数据，数据由 \(m\) 个操作构成，他知道这样的数据肯定打垮 spaly，但是国王还有很多很多其他的事情要做，所以统计每个操作所需要的实际代价的任务就交给你啦。

数据中的操作分为五种：

1. 插入操作：向当前非空 spaly 中插入一个关键码为 \(\mathrm{key}\) 的新孤立节点。插入方法为，先让 \(\mathrm{key}\) 和根比较，如果 \(\mathrm{key}\) 比根小，则往左子树走，否则往右子树走，如此反复，直到某个时刻，\(\mathrm{key}\) 比当前子树根 \(x\) 小，而 \(x\) 的左子树为空，那就让 \(\mathrm{key}\) 成为 \(x\) 的左孩子；
   
   或者 \(\mathrm{key}\) 比当前子树根 \(x\) 大，而 \(x\) 的右子树为空，那就让 \(\mathrm{key}\) 成为 \(x\) 的右孩子。该操作的代价为：插入后，\(\mathrm{key}\) 的深度。特别地，若树为空，则直接让新节点成为一个单个节点的树。（各节点关键码互不相等。对于「深度」的解释见末尾对 spaly 的描述）。
2. 单旋最小值：将 spaly 中关键码最小的元素 \(\mathrm{xmin}\) 单旋到根。操作代价为：单旋前 \(\mathrm{xmin}\) 的深度。（对于单旋操作的解释见末尾对 spaly 的描述）。
3. 单旋最大值：将 spaly 中关键码最大的元素 \(\mathrm{xmax}\) 单旋到根。操作代价为：单旋前 \(\mathrm{xmax}\) 的深度。
4. 单旋删除最小值：先执行 2 号操作,然后把根删除。由于 2 号操作之后,根没有左子树,所以直接切断根和右子树的联系即可（具体见样例解释）。 操作代价同 2 号操
   
   作。
5. 单旋删除最大值：先执行 3 号操作,然后把根删除。 操作代价同 3 号操作。

对于不是 H 国的人，你可能需要了解一些 spaly 的知识，才能完成国王的任务：

• spaly 是一棵二叉树，满足对于任意一个节点 \(x\)，它如果有左孩子 \(\mathrm{lx}\)，那么 \(\mathrm{lx}\) 的关键码小于 \(x\) 的关键码。如果有右孩子 \(\mathrm{rx}\)，那么 \(\mathrm{rx}\) 的关键码大于 \(x\) 的关键码。

• 一个节点在 spaly 的深度定义为：从根节点到该节点的路径上一共有多少个节点（包括自己）。

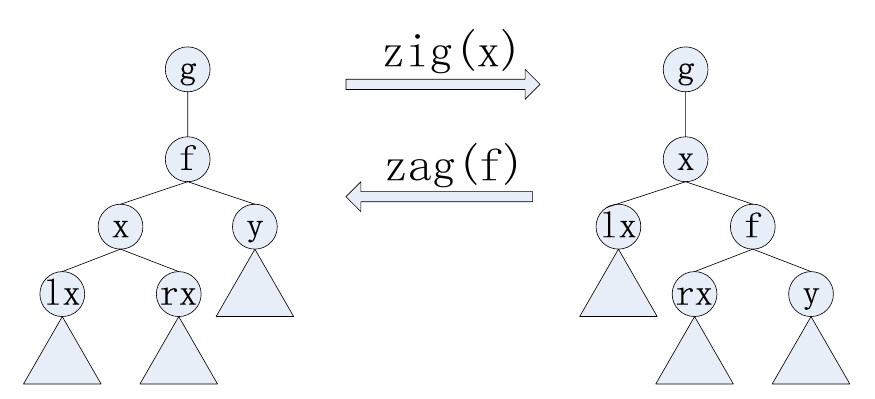
• 单旋操作是对于一棵树上的节点 \(x\) 来说的。一开始,设 \(f\) 为 \(x\) 在树上的父亲。如果 \(x\) 为 \(f\) 的左孩子，那么执行 \(\mathrm{zig}(x)\) 操作（如上图中，左边的树经过 \(\mathrm{zig}(x)\) 变为了右边的树），否则执行 \(\mathrm{zag}(x)\) 操作（在上图中，将右边的树经过 \(\mathrm{zag}(f)\) 就变成了左边的树）。每当执
  
  行一次 \(\mathrm{zig}(x)\) 或者 \(\mathrm{zag}(x)\)，\(x\) 的深度减小 \(1\)，如此反复，直到 \(x\) 为根。总之，单旋 \(x\) 就是通过反复执行 \(\mathrm{zig}\) 和 \(\mathrm{zag}\) 将 \(x\) 变为根。

  样例输入

  5
  1 2
  1 1
  1 3
  4
  5
  

  样例输出

  1
  2
  2
  2
  2
  

\(1≤m≤10^5,1≤key≤10^9\)

做这种看起来很怪很不可做的题的关键是要发现特殊性质。

因为这道题只对最大/最小值进行单旋操作，我们就会发现每次操作只会\(zig\)或者只会\(zag\)。

以最小值\(x\)为例，只会进行\(zig\)操作。操作完了过后，原来\(x\)的右儿子深度不变，\(x\)的深度变为\(1\)，其他部分\(+1\)。并且\(x\)的右儿子的排名一定是连续的。所以我们就可以使用线段树了。

插入的时候我们找到前驱和后继，深度较深的那个就是父节点。

代码：

#include<bits/stdc++.h>
#define ll long long
#define N 100005

using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}

int m;
int key[N],tot;
int ch[N][2],fa[N];
bool isleaf(int v) {return !ch[v][0]&&!ch[v][1];}
set<int>::iterator it;
set<int>pos;
int rt;
map<int,int>id;

struct segment_tree {
	int rt,ls[N*100],rs[N*100],tag[N*100];
	int lx=0,rx=1e9;
	int cnt;
	void ADD(int &v,int old,int lx,int rx,int l,int r,int f) {
		if(lx>r||rx<l) return ;
		v=++cnt;
		ls[v]=ls[old],rs[v]=rs[old];
		tag[v]=tag[old];
		if(l<=lx&&rx<=r) {tag[v]+=f;return ;}
		int mid=lx+rx>>1;
		ADD(ls[v],ls[old],lx,mid,l,r,f);
		ADD(rs[v],rs[old],mid+1,rx,l,r,f);
	}
	void ADD(int l,int r,int f) {ADD(rt,rt,lx,rx,l,r,f);}
	int query(int v,int lx,int rx,int p) {
		if(!v) return 0;
		if(lx==rx) return tag[v];
		int mid=lx+rx>>1;
		if(p<=mid) return query(ls[v],lx,mid,p)+tag[v];
		else return query(rs[v],mid+1,rx,p)+tag[v];
	}
	int query(int v) {return query(rt,lx,rx,v);}
}T;

void Splay_mn() {
	int x=id[*pos.begin()];
	int dep=T.query(key[x]);
	if(fa[x]) {
		T.ADD(0,1e9,1);
		if(key[x]<key[fa[x]]) T.ADD(key[x]+1,key[fa[x]]-1,-1);
		T.ADD(key[x],key[x],1-T.query(key[x]));
		fa[ch[x][1]]=fa[x];
		ch[fa[x]][0]=ch[x][1];
		ch[x][1]=rt;
		fa[rt]=x,fa[x]=0;
		rt=x;
	}
	cout<<dep<<"\n";
}

void Splay_mx() {
	int x=id[*(--pos.end())];
	int dep=T.query(key[x]);
	if(fa[x]) {
		T.ADD(0,1e9,1);
		if(key[x]>key[fa[x]]) T.ADD(key[fa[x]]+1,key[x]-1,-1);
		T.ADD(key[x],key[x],1-T.query(key[x]));
		fa[ch[x][0]]=fa[x];
		ch[fa[x]][1]=ch[x][0];
		ch[x][0]=rt;
		fa[rt]=x,fa[x]=0;
		rt=x;
	}
	cout<<dep<<"\n";
}

int main() {
	id[0]=0;
	m=Get();
	int op;
	while(m--) {
		op=Get();
		if(op==1) {
			key[++tot]=Get();
			id[key[tot]]=tot;
			int dep=0;
			if(!pos.size()) {
				pos.insert(key[tot]);
				rt=tot;
			} else {
				int x=0,y=0;
				it=pos.lower_bound(key[tot]);
				if(it!=pos.end()) x=*it;
				if(it!=pos.begin()) y=*(--it);
				if(!x||!y) {
					x=id[x+y];
				} else {
					x=id[x],y=id[y];
					if(T.query(key[x])<T.query(key[y])) x=y;
				}
				dep=T.query(key[x]);
				fa[tot]=x;
				if(key[tot]>key[x]) ch[x][1]=tot;
				else ch[x][0]=tot;
				T.ADD(key[tot],key[tot],1);
			}
			pos.insert(key[tot]);
			T.ADD(key[tot],key[tot],dep+1-T.query(key[tot]));
			cout<<dep+1<<"\n";
		} else if(op==2) {
			Splay_mn();
		} else if(op==3) {
			Splay_mx();
		} else if(op==4) {
			Splay_mn();
			pos.erase(key[rt]);
			rt=ch[rt][1];
			fa[rt]=0;
			T.ADD(0,1e9,-1);
		} else {
			Splay_mx();
			pos.erase(key[rt]);
			rt=ch[rt][0];
			fa[rt]=0;
			T.ADD(0,1e9,-1);
		}
	}
	return 0;
}