全网第二好懂的FFT（快速傅里叶变换）

声明：本FFT是针对OI的。专业人员请出门左拐。

Ⅰ前言

很久以前，我打算学习FFT。

然而，算法导论讲的很详细，却看不懂。网上博客更别说了，什么频率之类的都来了。我暗自下了决心：写一篇人看得懂的FFT

今天讲了FFT，我对这精（xuan）妙（xue）的算法有了初步的认识。我想，我如愿以偿了。

由于此算法不好理解的主要原因是涉及大量数学知识，所以我会尽量讲的浅显一点，以会写代码为目的。部分高超的证明会略去。

Ⅱ算法简介

快速傅里叶变换，FFT（Fast-Fast TLE,Fast Fourier Transform），是一种高效的多项式系数点值互换的算法（不懂没关系，一会儿要讲）。最广泛的应用是计算多项式乘法。

通常，暴力展开复杂度为O（$n^{2}$）。而FFT则可以达到O(nlogn)

辣么我们开始吧。

Ⅲ前置知识(顺便简单提一下流程，后面流程详细讲）

1.多项式

回忆一下初中多项式的定义：

由若干个单项式相加组成的代数式叫做多项式。

单项式又是啥？

由数或字母的积组成的代数式叫做单项式。

low爆了！

我们已经是高中生了什么时候的事我怎么不知道，我们换一种定义：

多项式   :=   f(x)=$\sum_{i=0}^{n-1}a_{i}x^{i}\qquad$

其中n称为次数。

怎么样？有没有莫比乌斯反演的既视感？

2.多项式的表示方法

上面提到的叫做系数表达式。其实多项式还有一种表示：点值表达式。

标准定义找不到啊qwq

那这么说吧：

先把多项式看做一个函数，画出它的图像

然后在上面任取n个不同的点

那么这三个点就可以唯一的确定这个多项式。至于为什么唯一，通过意识流很容易证明。

为什么要引入这个东西呢？因为如果把两个多项式转换为x相同的点值，就可以O（n）求出它们的乘积。太神奇啦！

辣么现在问题就成了：如何把原多项式转成点值，再把乘出来的点值转系数。

最直观的方法：把原多项式转成点值就取几个值，点值转系数可以高斯消元。

于是尴尬的事情发生了：

总复杂度O（$n^{3}$）

看来还要想办法啊。

3.弧度制和任意三角函数（学过的往后跳）

初中的三角函数是针对锐角的。那其他角有没有三角函数呢？

当然啦。

这要从任意角说起。

高中我们定义角为一条射线（一般指x正半轴）逆时针旋转后（称为终边）与原来的射线形成的图形，允许有负数，即顺时针

所以，这是个角：

这也是个角，而且和上一个不同：

这还是个角，而且是负角：

这仍然是个角：

好吧。。。

以前用角都是有单位，即1°=一个周角的1/360

那能不能换一个没单位的呢？

定义弧度为这个角所对弧长与半径的比，这样角就是一个常数。

很容易知道，一个周角是2π弧度。即π弧度对应180°。（前面那个是圆周率  垃圾markdown）

这样任意角三角函数就出来了：

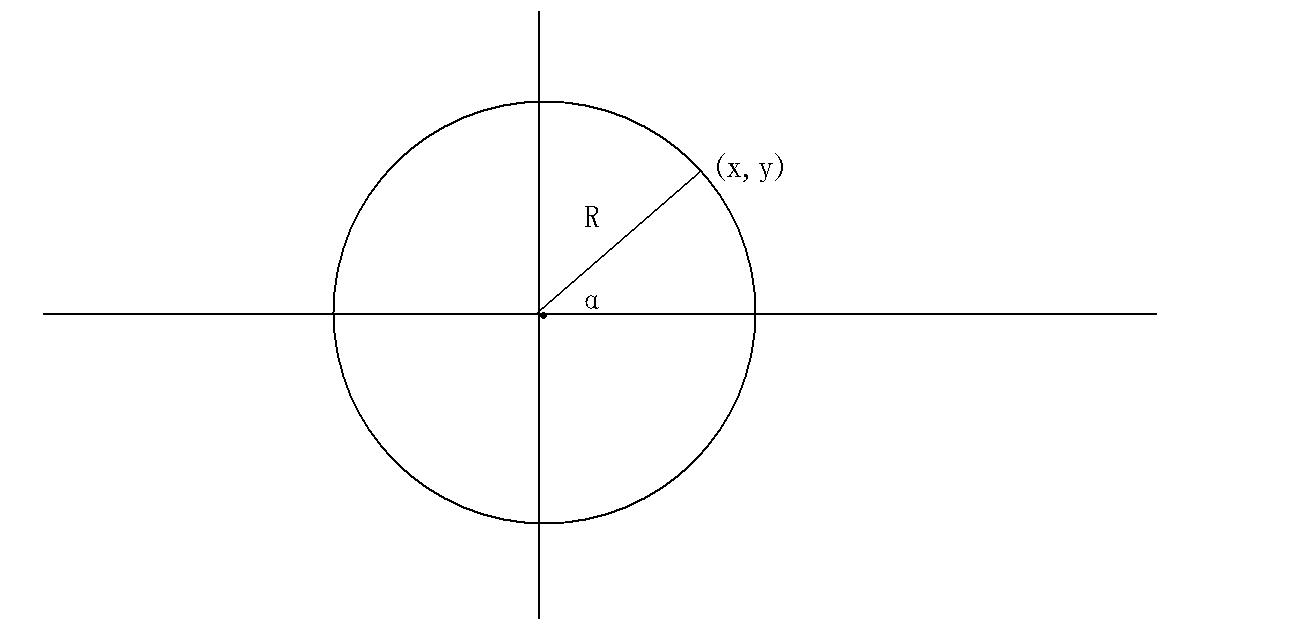
在直角坐标系中，以O为圆心作一个半径为R的圆。角α的终边与圆的交点坐标（x，y），那么有

sinα=$\frac{x}{R}$

cosα=$\frac{y}{R}$

其他三角函数类似，但FFT用不到，就不说了

4.复数与单位根

实数貌似没什么特殊性质。那实数之外呢？

我们定义$i^{2}$=-1。任何复数（也就是目前的所有数）都可以表示成x+yi的形式（x，y均为实数）

等等！这不是没有意义吗？这是什么鬼玩意儿？

好吧，你可以不管它。就把它看成这个：

 struct complex
 {
     double x,y;
 };

就好了。

当然它的乘法就是把它拆开，$i^{2}$换成-1，i保留就好了。(不懂没关系，后面看代码）

由于是两个实数，所以我们可以yy出一个平面：x代表实部，y代表虚部。这上面的点都是与复数一一对应的。

单位根就是满足$w^{n}$=1的所有复数，共n个，记为$w_{n}$（注：这里的w应该是个希腊字母，但为了偷懒就用w代替）

根据意识流在复平面上，这n个点与原点连线长度相同，且平分圆周。

并且，它们是$w_{n}$,$w_{n}^{2}$,$w_{n}^{3}$......$w_{n}^{n}$的关系，我们就这么表示好了

你可以用上面的性质把n个单位根算出来

即$w_{n}^{k}$=cos$\frac{2πk}{n}$+sin$\frac{2πk}{n}$i

Ⅳ算法流程

我们假装n是2的k次幂 即$n=2^{k}$，k为非负整数

令x=$w_{n}^{k}$,代入多项式

（注：1.如果你不想看，并且你可以在不理解的情况下背代码，可以跳过以下推导  2.以下的i都是循环变量而不是虚数单位）

$F(w_{n}^{k})=\sum_{i=0}^{n-1}a_{i}w_{n}^{ik}$

闲着没事，把它按奇偶分类：

$F(w_{n}^{k})=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{n}^{2ik}+a_{2i+1}w_{n}^{(2i+1)k}$

看后面那坨不顺眼

$F(w_{n}^{k})=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{n}^{2ik}+w_{n}^{k}a_{2i+1}w_{n}^{2ik}$

根据折半引理：

$(w_{n}^{k})^{2}=w_{\frac{n}{2}}^{k}$

可得：

$F(w_{n}^{k})=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{\frac{n}{2}}^{ik}+w_{n}^{k}a_{2i+1}w_{\frac{n}{2}}^{ik}$

有没有一种似曾相识的感觉呢？

所以可以递归下去：（type干啥的马上就知道了）

const double PI=acos(-1.0);
struct complex
{
    double x,y;
    complex(double x=,double y=):x(x),y(y){}
}a[MAXN],b[MAXN];
complex operator +(const complex& a,const complex& b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(const complex& a,const complex& b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(const complex& a,const complex& b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
void fft(int lim,complex *a,int type)
{
    if (lim==)
        return;
    complex a1[lim>>],a2[lim>>];
    for (int i=;i<=lim;i+=)
        a1[i>>]=a[i],a2[i>>]=a[i+];
    fft(lim>>,a1,type);
    fft(lim>>,a2,type);
    complex wn(cos(2.0*PI/lim),type*sin(2.0*PI/lim)),w(,);
    for (int i=;i<(lim>>);i++,w=w*wn)
    {
        a[i]=a1[i]+w*a2[i];
        a[i+(lim>>)]=a1[i]-w*a2[i];
    }
}

于是 就完了？

怎么可能？

上面只是系数转点值。而平时点值很少用，即使用也不会是复数啊……

所以还要把点值转系数。我们称为傅里叶逆变换。

又是推式子的时间啦！

（其实这里我也不怎么懂……但结论很简单，直接记就行）

我们设$c_{i}$为多项式在$w_{n}^{-i}$的点值表达式（也就是y值），其中$0<=i<n$LaTeX可以美化呢

即

　　$c_{k}=\sum_{i=0}^{n-1}y_{i}(w_{n}^{-k})^{i}$

把$y_{i}$拆开

　　$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_{j}(w_{n}^{i})^{j})(w_{n}^{-k})^{i})$

你到前面来

　　$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_{j}(w_{n}^{j})^{i})(w_{n}^{-k})^{i})$

辣眼睛的小括号

　　$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_{j}(w_{n}^{j})^{i}(w_{n}^{-k})^{i}$

咦？

　　$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_{j}(w_{n}^{j-k})^{i}$

瞎搞一波

　　$=\sum_{i=0}^{n-1}a_{j}(\sum_{j=0}^{n-1}(w_{n}^{j-k})^{i})$

设$S(x)=\sum_{i=0}^{n-1}x$

代入

$S(w_{n}^{k})=1+(w_{n}^{k})+(w_{n}^{k})^{2}+... ... +(w_{n}^{k})^{n-1}$

当k不为0时，运用你丰富的等比数列知识

$S(w_{n}^{k})=\frac{(w_{n}^{k})^{n}-1}{(w_{n}^{k})-1}$

$S(w_{n}^{k})=0$

k=0时，显然$S(w_{n}^{k})=n$

回到刚刚的式子，发现：

$=\sum_{i=0}^{n-1}a_{j}(\sum_{j=0}^{n-1}(w_{n}^{j-k})^{i})$

当$j=k$时，为n

当$j \neq k$时，为0

即

$c_{k}=na_{k}$

$a_{k}=\frac{a_{k}}{n}$

也就是把上面的type改成-1，然后答案除以lim就好了

完整代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cctype>
#define MAXN 2000005
const double PI=acos(-1.0);
using namespace std;
inline int read()
{
    int ans=0,f=1;
    char c=getchar();
    while (!isdigit(c))
    {
        if (c=='-')
            f=-1;
        c=getchar();
    }
    while (isdigit(c))
    {
        ans=(ans<<3)+(ans<<1)+(c^48);
        c=getchar();
    }
    return f*ans;
}
struct complex
{
    double x,y;
    complex(double x=0,double y=0):x(x),y(y){}
}a[MAXN],b[MAXN];
complex operator +(const complex& a,const complex& b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(const complex& a,const complex& b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(const complex& a,const complex& b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
void fft(int lim,complex *a,int type)
{
    if (lim==1)
        return;
    complex a1[lim>>1],a2[lim>>1];
    for (int i=0;i<=lim;i+=2)
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fft(lim>>1,a1,type);
    fft(lim>>1,a2,type);
    complex wn(cos(2.0*PI/lim),type*sin(2.0*PI/lim)),w(1,0);
    for (int i=0;i<(lim>>1);i++,w=w*wn)
    {
        a[i]=a1[i]+w*a2[i];
        a[i+(lim>>1)]=a1[i]-w*a2[i];
    }
}
int main()
{
    int n,m;
    n=read(),m=read();
    for (int i=0;i<=n;i++)//注意下标
        a[i].x=read();
    for (int i=0;i<=m;i++)
        b[i].x=read();
    int lim=1;
    while (lim<=n+m)
        lim<<=1;
    fft(lim,a,1);
    fft(lim,b,1);
    for (int i=0;i<=lim;i++)
        a[i]=a[i]*b[i];
    fft(lim,a,-1);
    for (int i=0;i<=n+m;i++)
        printf("%d ",(int)(a[i].x/lim+0.5));
    return 0;
}

　　

 V.改进

什么？你T了？

不会吧我都是RE

那我们换一种实现？

（侵删）

不难看出，原序列和后序列二进制是反转的

然后就可以AC此题

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cctype>
#define MAXN 10000010
const double PI=acos(-1.0);
using namespace std;
inline int read()
{
    int ans=0,f=1;
    char c=getchar();
    while (!isdigit(c))
    {
        if (c=='-')
            f=-1;
        c=getchar();
    }
    while (isdigit(c))
    {
        ans=(ans<<3)+(ans<<1)+(c^48);
        c=getchar();
    }
    return f*ans;
}
struct complex
{
    double x,y;
    complex(double x=0,double y=0):x(x),y(y){}
}a[MAXN],b[MAXN];
complex operator +(const complex& a,const complex& b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(const complex& a,const complex& b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(const complex& a,const complex& b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
int lim=1;
int l,r[MAXN];
void fft(complex *a,int type)
{
    for (int i=0;i<lim;i++)
        if (i<r[i])
            swap(a[i],a[r[i]]);
    for (int mid=1;mid<lim;mid<<=1)//非<=
    {
        complex wn(cos(PI/mid),type*sin(PI/mid));
        for (int R=mid<<1,j=0;j<lim;j+=R)
        {
            complex w(1,0);
            for (int k=0;k<mid;k++,w=w*wn)
            {
                complex x=a[j+k],y=w*a[j+k+mid];
                a[j+k]=x+y;
                a[j+k+mid]=x-y;
            }
        }
    }
}
int main()
{
    int n,m;
    n=read(),m=read();
    for (int i=0;i<=n;i++)//注意下标
        a[i].x=read();
    for (int i=0;i<=m;i++)
        b[i].x=read();
    while (lim<=n+m)
        lim<<=1,l++;
    for (int i=0;i<lim;i++)
        r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
    fft(a,1);
    fft(b,1);
    for (int i=0;i<=lim;i++)
        a[i]=a[i]*b[i];
    fft(a,-1);
    for (int i=0;i<=n+m;i++)
        printf("%d ",(int)(a[i].x/lim+0.5));
    return 0;
}