Codeforces Round #393 (Div. 2) (8VC Venture Cup 2017 - Final Round Div. 2 Edition)A 水 B 二分 C并查集

A. Petr and a calendar

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Petr wants to make a calendar for current month. For this purpose he draws a table in which columns correspond to weeks (a week is seven consequent days from Monday to Sunday), rows correspond to weekdays, and cells contain dates. For example, a calendar for January 2017 should look like on the picture:

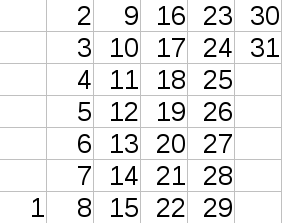
Petr wants to know how many columns his table should have given the month and the weekday of the first date of that month? Assume that the year is non-leap.

Input

The only line contain two integers m and d (1 ≤ m ≤ 12, 1 ≤ d ≤ 7) — the number of month (January is the first month, December is the twelfth) and the weekday of the first date of this month (1 is Monday, 7 is Sunday).

Output

Print single integer: the number of columns the table should have.

Examples

input

1 7

output

6

input

1 1

output

5

input

11 6

output

5

Note

The first example corresponds to the January 2017 shown on the picture in the statements.

In the second example 1-st January is Monday, so the whole month fits into 5 columns.

In the third example 1-st November is Saturday and 5 columns is enough.

题意：2017第m个月 当月第一天是星期d 问这个月的日历需要几列

题解：水

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <stack>
 #include <queue>
 #include <cmath>
 #include <map>
 #define ll  __int64
 #define mod 1000000007
 #define dazhi 2147483647
 using namespace  std;
 int m,d;
 int main()
 {
     int ans=;
     int exm;
     scanf("%d %d",&m,&d);
     if(m==||m==||m==||m==||m==||m==||m==)
     exm=;
     else
     {
         if(m==)
           exm=;
         else
           exm=;
     }
     exm=exm-(-d+);
     ans=ans+exm/;
     if(exm%)
         ans++;
     cout<<ans<<endl;
     return ;
 }

B. Frodo and pillows

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

n hobbits are planning to spend the night at Frodo's house. Frodo has n beds standing in a row and m pillows (n ≤ m). Each hobbit needs a bed and at least one pillow to sleep, however, everyone wants as many pillows as possible. Of course, it's not always possible to share pillows equally, but any hobbit gets hurt if he has at least two pillows less than some of his neighbors have.

Frodo will sleep on the k-th bed in the row. What is the maximum number of pillows he can have so that every hobbit has at least one pillow, every pillow is given to some hobbit and no one is hurt?

Input

The only line contain three integers n, m and k (1 ≤ n ≤ m ≤ 10⁹, 1 ≤ k ≤ n) — the number of hobbits, the number of pillows and the number of Frodo's bed.

Output

Print single integer — the maximum number of pillows Frodo can have so that no one is hurt.

Examples

input

4 6 2

output

2

input

3 10 3

output

4

input

3 6 1

output

3

Note

In the first example Frodo can have at most two pillows. In this case, he can give two pillows to the hobbit on the first bed, and one pillow to each of the hobbits on the third and the fourth beds.

In the second example Frodo can take at most four pillows, giving three pillows to each of the others.

In the third example Frodo can take three pillows, giving two pillows to the hobbit in the middle and one pillow to the hobbit on the third bed.

题意：n个床 m个垫子 Frodo 在第k个床上 要求相邻的两个床的相差的垫子的个数不能超过1 每个床上最少要有一个垫子  问 满足情况下 Frodo的床上最多有多少垫子

题解：二分Frodo床上的垫子数量 check 是否满足  很容想到以Frodo所在的床为中点向左向右的垫子数量都是递减的

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <stack>
 #include <queue>
 #include <cmath>
 #include <map>
 #define ll  __int64
 #define mod 1000000007
 #define dazhi 2147483647
 using namespace  std;
 ll n,m,k;
 ll fun(ll x)
 {
     x=x-;
     ll exm1,exm2,exm3;
     exm1=(+x)*x/;
     if((x-k)<=)
      exm2=;
     else{
         if((x-k)==)
             exm2=;
         else
             exm2=(+x-k)*(x-k)/;
     }
     if((x-(n-k+))<=)
      exm3=;
     else{
         if((x-(n-k+))==)
             exm3=;
         else
             exm3=(+(x-(n-k+)))*(x-(n-k+))/;
     }
     return n+exm1-exm2+exm1-exm3-x;
 }
 int main()
 {
     scanf("%I64d %I64d %I64d",&n,&m,&k);
     ll l=,r=1e9,mid;
      while(l<r)
      {
          mid=(l+r)>>;
          if(fun(mid)<=m)
             l=mid+;
          else
             r=mid;
      }
      if(fun(l)<=m)
         cout<<l<<endl;
      else
         cout<<l-<<endl;
     return ;
 }

C. Pavel and barbecue

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Pavel cooks barbecue. There are n skewers, they lay on a brazier in a row, each on one of n positions. Pavel wants each skewer to be cooked some time in every of n positions in two directions: in the one it was directed originally and in the reversed direction.

Pavel has a plan: a permutation p and a sequence b₁, b₂, ..., b_n, consisting of zeros and ones. Each second Pavel move skewer on position i to position p_i, and if b_i equals 1 then he reverses it. So he hope that every skewer will visit every position in both directions.

Unfortunately, not every pair of permutation p and sequence b suits Pavel. What is the minimum total number of elements in the given permutation p and the given sequence b he needs to change so that every skewer will visit each of 2n placements? Note that after changing the permutation should remain a permutation as well.

There is no problem for Pavel, if some skewer visits some of the placements several times before he ends to cook. In other words, a permutation p and a sequence b suit him if there is an integer k (k ≥ 2n), so that after k seconds each skewer visits each of the 2nplacements.

It can be shown that some suitable pair of permutation p and sequence b exists for any n.

Input

The first line contain the integer n (1 ≤ n ≤ 2·10⁵) — the number of skewers.

The second line contains a sequence of integers p₁, p₂, ..., p_n (1 ≤ p_i ≤ n) — the permutation, according to which Pavel wants to move the skewers.

The third line contains a sequence b₁, b₂, ..., b_n consisting of zeros and ones, according to which Pavel wants to reverse the skewers.

Output

Print single integer — the minimum total number of elements in the given permutation p and the given sequence b he needs to change so that every skewer will visit each of 2n placements.

Examples

input

4
4 3 2 1
0 1 1 1

output

2

input

3
2 3 1
0 0 0

output

1

Note

In the first example Pavel can change the permutation to 4, 3, 1, 2.

In the second example Pavel can change any element of b to 1.

题意：Pavel有n个地点烤肉，给你个数组p，p[i]代表可以从第i个位置到第p[i]个位置，p数组为n的一个全排列，又有个数组b，b[i]为1的时候，当Pavel走到第i个位置必须把这里的烤肉翻面。Pavel可以改变p数组或者b数组上的任意一个元素。问Pavel至少要改变多少个元素使得他可以把所有烤肉正反两面都烤一次。

题解：这题其实就是要先把路径改成一个环，因为只有成了环，Pavel才能走完两圈。由于p是全排列，因此这个路径本身就是一个或者多个环组合而成的。我们考虑n个环之间要合并，需要改动n条边，所以可以并查集或者dfs出环（联通块）的数量，这就是p数组需要改变的元素个数。然后我们考虑，假设最后合并成的环上，如果有奇数个1，Pavel就可以正反都烤到肉，如果是偶数个1就不行，因此判断下1的个数的奇偶性，就能得出b数组要改变多少次。需要特判环数为1的时候，p数组不需要改变。

#其实并不是很懂题意 看的别人的解释 orzzz#

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <stack>
 #include <queue>
 #include <cmath>
 #include <map>
 #define ll  __int64
 #define mod 1000000007
 #define dazhi 2147483647
 using namespace  std;
 int n;
 int p[];
 int b[];
 int fa[];
 int ans=;
 int exm=;
 int sum=;
 int find(int root)
 {
     if(fa[root]!=root)
         return fa[root]=find(fa[root]);
     else
         return root;
 }
 void uni(int a,int b)
 {
     int aa,bb;
     aa=find(a);
     bb=find(b);
     if(aa!=bb){
         fa[aa]=bb;
         sum--;
         }
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=; i<=n; i++)
         scanf("%d",&p[i]);
     for(int i=; i<=n; i++)
     {
         scanf("%d",&b[i]);
         if(b[i]==)
             exm++;
     }
     sum=n;
     for(int i=; i<=n; i++)
         fa[i]=i;
     for(int i=; i<=n; i++)
         uni(p[i],i);
     if(sum==) sum=;
     if(exm%==)
         sum++;
     printf("%d\n",sum);
     return ;
 }