manim边学边做--通用多边形

manim提供了通用多边形模块，可以绘制任意的多边形。

通用多边形模块有两种，Polygon和Polygram。

Polygon是一个几何学术语，主要指的是由三条或三条以上的线段首尾顺次连接所组成的平面图形，

而Polygram的含义更加广泛一些，它除了可以绘制传统的多边形，还能绘制非闭合的多边形，各部分不相连的多边形等等。

对于一般的几何问题，使用Polygon就足够了，只有在需要表达一些图形的组合或序列时，才会用到Polygram。

manim中关于Polygon和Polygram的模块主要有4个：

1. Polygon：任意多边形
2. RegularPolygon：任意正多边形
3. Polygram：广义的多边形
4. RegularPolygram：广义的正多边形

Polygon和Polygram其实也可以绘制正多边形，只不过用RegularPolygon和RegularPolygram会更加方便。

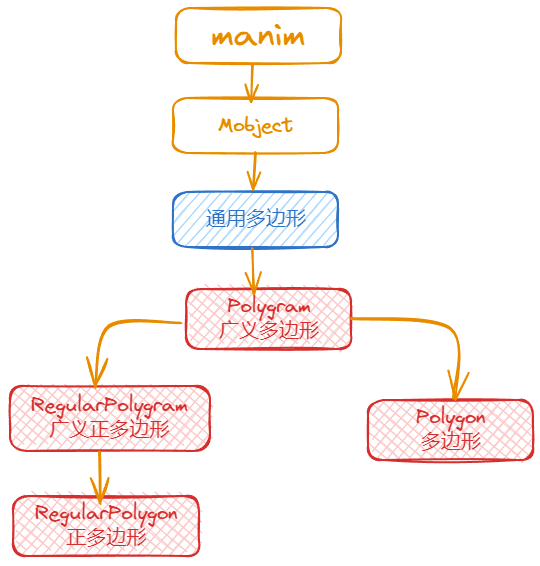
这4个模块的继承关系如上图所示。

1. 主要参数

Polygon的参数很简单，就是提供一系列的顶点坐标。

绘制时会依照提供的顶点顺序依次连线，最后一个点会连接第一个点，形成一个闭合的多边形。

参数名称	类型	说明
vertices	Point3D	多边形的顶点列表

RegularPolygon的参数也很简单：

参数名称	类型	说明
n	int	正多边形的边数

Polygram的参数是多组的顶点，每组有多个顶点，与之相比，Polygon的参数只有一组顶点。

参数名称	类型	说明
vertex_groups	Point3D	多组顶点列表，如果只有一组顶点，那么图形和Polygon一样

RegularPolygram的参数有：

参数名称	类型	说明
num_vertices	int	顶点的个数
radius	float	图形外接圆的半径
density	int	跳跃多少个顶点来连接
start_angle	float	第一个顶点的角度

RegularPolygon比较简单，就是顺序连接各个顶点形成多边形，

而RegularPolygram有个density参数，可以控制跳跃几个顶点来连接。

设置density=1的话，RegularPolygram和RegularPolygon的图形是一样的，后面示例中详细演示。

2. 主要方法

Polygram作为最通用的多边形，提供了3个方法。

名称	说明
get_vertex_groups	以分组的形式获取多变形的所有顶点坐标
get_vertices	获取多变形的所有顶点坐标
round_corners	调整多边形角的曲率

get_vertex_groups和get_vertices主要区别在于：

get_vertex_groups以分组的形式返回顶点坐标，这对于Polygram模块比较有用，因为Polygram模块的参数可以传入多组顶点；

get_vertices则是将所有的坐标作为一个列表返回出来。

round_corners用来调整多边形尖角的曲率。

# 创建3个广义正六边形
p1 = RegularPolygram(6)
p2 = RegularPolygram(6)
p3 = RegularPolygram(6)

# p2的尖角曲率设为0.1
p2.round_corners(radius=0.1)

# p3的尖角曲率设为0.3
p3.round_corners(radius=0.3)

其他3个模块没有什么重要的方法。

3. 使用示例

3.1. 多边形示例

多变形就是按照传入的顶点的顺序逐个连接成一个闭合图形。

# 凸多边形
points = [
    LEFT * 2.5,
    LEFT * 1.5 + UP,
    LEFT * 0.5,
    LEFT * 0.5 + DOWN * 1.5,
    LEFT * 2.5 + DOWN * 1.5,
]
Polygon(*points)

# 凹多边形
points = [
    RIGHT * 0.5 + UP,
    RIGHT * 1.5 + DOWN,
    RIGHT * 2.5 + UP,
    RIGHT * 2.5 + DOWN * 1.5,
    RIGHT * 0.5 + DOWN * 1.5,
]
Polygon(*points)

3.2. 正多边形

正多边形最简单，只要传入边的数量即可。

RegularPolygon(n=6)
RegularPolygon(n=8)
RegularPolygon(n=12)

3.3. 广义多边形

广义多边形更像是多个多边形的组合，它可以传入多个组的的顶点，然后根据每个组的顶点来构造图形。

下面的示例中，第一个图形有3个组顶点，第二个图形有2个组顶点。

group_points = [
    [[-2.5,0,0], [-1.5,1,0], [-0.5,0,0]],
    [[-2,0,0], [-2,-1.5,0]],
    [[-1,0,0], [-1,-1.5,0]],
]
Polygram(*group_points)

group_points = [
    [[0.5,0,0], [1.5,1,0], [2.5,0,0]],
    [[0.5,-1,0], [1.5,0,0], [2.5,-1,0]],
]
Polygram(*group_points)

3.4. 广义正多边形

广义正多边形可以调整顶点的连接顺序（通过属性density），逐个连接时，和普通正多边形是一样的。

# 正九边形，逐个连接顶点
RegularPolygram(9, density=1)

# 正九边形，隔一个顶点连接
RegularPolygram(9, density=2)

# 正九边形，隔两个顶点连接
RegularPolygram(9, density=3)

4. 附件

文中完整的代码放在网盘中了（polygon02.py），

下载地址: 完整代码 (访问密码: 6872)