神经网络优化篇：理解mini-batch梯度下降法（Understanding mini-batch gradient descent）

理解mini-batch梯度下降法

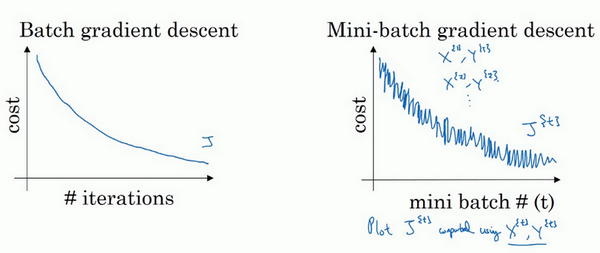
使用batch梯度下降法时，每次迭代都需要历遍整个训练集，可以预期每次迭代成本都会下降，所以如果成本函数\(J\)是迭代次数的一个函数，它应该会随着每次迭代而减少，如果\(J\)在某次迭代中增加了，那肯定出了问题，也许的学习率太大。

使用mini-batch梯度下降法，如果作出成本函数在整个过程中的图，则并不是每次迭代都是下降的，特别是在每次迭代中，要处理的是\(X^{\{t\}}\)和\(Y^{\{ t\}}\)，如果要作出成本函数\(J^{\{ t\}}\)的图，而\(J^{\{t\}}\)只和\(X^{\{ t\}}\)，\(Y^{\{t\}}\)有关，也就是每次迭代下都在训练不同的样本集或者说训练不同的mini-batch，如果要作出成本函数\(J\)的图，很可能会看到这样的结果，走向朝下，但有更多的噪声，所以如果作出\(J^{\{t\}}\)的图，因为在训练mini-batch梯度下降法时，会经过多代，可能会看到这样的曲线。没有每次迭代都下降是不要紧的，但走势应该向下，噪声产生的原因在于也许\(X^{\{1\}}\)和\(Y^{\{1\}}\)是比较容易计算的mini-batch，因此成本会低一些。不过也许出于偶然，\(X^{\{2\}}\)和\(Y^{\{2\}}\)是比较难运算的mini-batch，或许需要一些残缺的样本，这样一来，成本会更高一些，所以才会出现这些摆动，因为是在运行mini-batch梯度下降法作出成本函数图。

需要决定的变量之一是mini-batch的大小，\(m\)就是训练集的大小，极端情况下，如果mini-batch的大小等于\(m\)，其实就是batch梯度下降法，在这种极端情况下，就有了mini-batch \(X^{\{1\}}\)和\(Y^{\{1\}}\)，并且该mini-batch等于整个训练集，所以把mini-batch大小设为\(m\)可以得到batch梯度下降法。

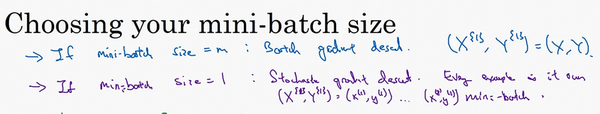
另一个极端情况，假设mini-batch大小为1，就有了新的算法，叫做随机梯度下降法，每个样本都是独立的mini-batch，当看第一个mini-batch，也就是\(X^{\{1\}}\)和\(Y^{\{1\}}\)，如果mini-batch大小为1，它就是的第一个训练样本，这就是的第一个训练样本。接着再看第二个mini-batch，也就是第二个训练样本，采取梯度下降步骤，然后是第三个训练样本，以此类推，一次只处理一个。

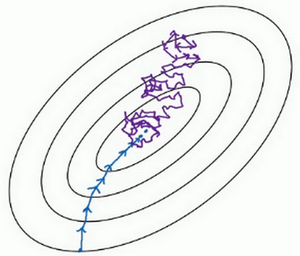
看在两种极端下成本函数的优化情况，如果这是想要最小化的成本函数的轮廓，最小值在那里，batch梯度下降法从某处开始，相对噪声低些，幅度也大一些，可以继续找最小值。

相反，在随机梯度下降法中，从某一点开始，重新选取一个起始点，每次迭代，只对一个样本进行梯度下降，大部分时候向着全局最小值靠近，有时候会远离最小值，因为那个样本恰好给指的方向不对，因此随机梯度下降法是有很多噪声的，平均来看，它最终会靠近最小值，不过有时候也会方向错误，因为随机梯度下降法永远不会收敛，而是会一直在最小值附近波动，但它并不会在达到最小值并停留在此。

实际上选择的mini-batch大小在二者之间，大小在1和\(m\)之间，而1太小了，\(m\)太大了，原因在于如果使用batch梯度下降法，mini-batch的大小为\(m\)，每个迭代需要处理大量训练样本，该算法的主要弊端在于特别是在训练样本数量巨大的时候，单次迭代耗时太长。如果训练样本不大，batch梯度下降法运行地很好。

相反，如果使用随机梯度下降法，如果只要处理一个样本，那这个方法很好，这样做没有问题，通过减小学习率，噪声会被改善或有所减小，但随机梯度下降法的一大缺点是，会失去所有向量化带给的加速，因为一次性只处理了一个训练样本，这样效率过于低下，所以实践中最好选择不大不小的mini-batch尺寸，实际上学习率达到最快。会发现两个好处，一方面，得到了大量向量化，上个视频中用过的例子中，如果mini-batch大小为1000个样本，就可以对1000个样本向量化，比一次性处理多个样本快得多。另一方面，不需要等待整个训练集被处理完就可以开始进行后续工作，再用一下上个视频的数字，每次训练集允许采取5000个梯度下降步骤，所以实际上一些位于中间的mini-batch大小效果最好。

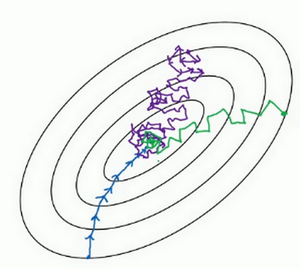
用mini-batch梯度下降法，从这里开始，一次迭代这样做，两次，三次，四次，它不会总朝向最小值靠近，但它比随机梯度下降要更持续地靠近最小值的方向，它也不一定在很小的范围内收敛或者波动，如果出现这个问题，可以慢慢减少学习率，在下个视频会讲到学习率衰减，也就是如何减小学习率。

如果mini-batch大小既不是1也不是\(m\)，应该取中间值，那应该怎么选择呢？其实是有指导原则的。

首先，如果训练集较小，直接使用batch梯度下降法，样本集较小就没必要使用mini-batch梯度下降法，可以快速处理整个训练集，所以使用batch梯度下降法也很好，这里的少是说小于2000个样本，这样比较适合使用batch梯度下降法。不然，样本数目较大的话，一般的mini-batch大小为64到512，考虑到电脑内存设置和使用的方式，如果mini-batch大小是2的\(n\)次方，代码会运行地快一些，64就是2的6次方，以此类推，128是2的7次方，256是2的8次方，512是2的9次方。所以经常把mini-batch大小设成2的次方。在上一个视频里，的mini-batch大小设为了1000，建议可以试一下1024，也就是2的10次方。也有mini-batch的大小为1024，不过比较少见，64到512的mini-batch比较常见。

最后需要注意的是在的mini-batch中，要确保\(X^{\{ t\}}\)和\(Y^{\{t\}}\)要符合CPU/GPU内存，取决于的应用方向以及训练集的大小。如果处理的mini-batch和CPU/GPU内存不相符，不管用什么方法处理数据，会注意到算法的表现急转直下变得惨不忍睹，所以希望对一般人们使用的mini-batch大小有一个直观了解。事实上mini-batch大小是另一个重要的变量，需要做一个快速尝试，才能找到能够最有效地减少成本函数的那个，一般会尝试几个不同的值，几个不同的2次方，然后看能否找到一个让梯度下降优化算法最高效的大小。希望这些能够指导如何开始找到这一数值。

学会了如何执行mini-batch梯度下降，令算法运行得更快，特别是在训练样本数目较大的情况下。