连续段 dp - 状态转移时依赖相邻元素的序列计数问题

引入

在一类序列计数问题中，状态转移的过程可能与相邻的已插入元素的具体信息相关。

这类问题通常的特点是，如果只考虑在序列的一侧插入，问题将容易解决。

枚举插入顺序的复杂度通常难以接受，转移时枚举插入位置又难以记录已插入元素的信息。

所以我们就要用连续段 dp。

dp 模型

连续段 dp 的好处在于，他的元素插入只会在连续段的两端进行。

所以他只会通过 建立新段，插入至已有连续段的两端，合并两段 来进行转移。

通常地，我们会按某种特定的顺序插入所有元素。

每次插入元素时，对三类转移方式进行分类讨论：

1. 将插入的元素作为一个新连续段插入
2. 将元素插入至一个已有连续段的两端
3. 将元素用于合并两个连续段

分别会导致什么状态变化。

我们先从最基础的 dp 模型说起。

求满足某些限制的 \(n\) 个元素的排列数量

我们一般会定义 \(dp_{i,j}\) 为前 \(i\)，形成了 \(j\) 个联通段的个数。

所以我们考虑三种情况。

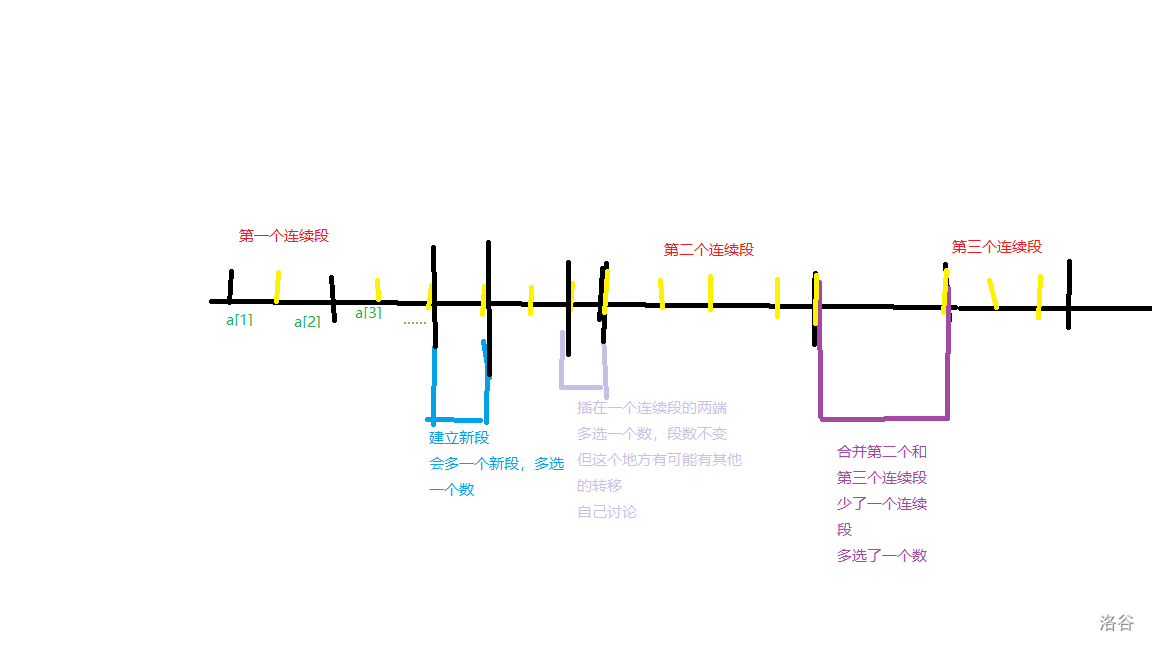
1. 建立新的连续段：\(dp_{i,j} \times (j + 1) \to dp_{i + 1,j + 1}\)
2. 合并两个连续段：\(dp_{i,j} \times (j - 1) \to dp_{i + 1,j - 1}\)
3. 插入至已有连续段的两端：\(dp_{i,j} \times 2 \times j \to dp_{i + 1,j}\)（注意此时有可能左右不同，所以要分讨）

可能有人会对转移方程有问题。我下面用一张直观一点的图做一个解释。

例题：

[COCI2021-2022#2] Magneti

考虑 DP。

令 \(g_k\) 为放完所有小球后还剩下 \(k\) 个空为的情况数。

所以容易推出 \(\sum^{m-n}_{k=0} g_k \times (^{n + m - k}_{\ \ \ \ \ \ k})\) 就是答案。

现在问题转化成了怎么求 \(g_k\)。

考虑 DP。

\(dp_{i,j,k}\) 表示放完前 \(i\) 个小球，有 \(j\) 个连续段，不能放球的位置有 \(k\) 个。

然后在上面的式子改一改即可。

1. \((j + 1) \times dp_{i,j,k} \to dp_{i + 1,j + 1,k + 1}\)

2. \((j - 1) \times dp_{i,j,k} \to dp_{i + 1,j - 1,k + 2\times r_{i+1} - 1}\)

3. \(dp_{i,j,k} \times 2 \times j \to dp_{i + 1,j,k + r_{i + 1}}\)

所以就有代码啦！

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 1e9 + 7;
const int maxn = 55;
const int maxl = 10000 + 100;
int n,l;
int r[maxn],g[maxl];
int dp[maxn][maxn][maxl];
int fac[maxl],inv[maxl];
int qpow(int a,int b)
{
    int res = 1;
    while(b)
    {
        if(b & 1)
        {
            res = res * a % mod;
        }
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}
int C(int a,int b)
{
    return fac[a] * inv[b] % mod * inv[a - b] % mod;
}
signed main()
{
    fac[0] = inv[0] = 1;
    for(int i = 1;i < maxl;i++)
    {
        fac[i] = fac[i - 1] * i % mod;
        inv[i] = qpow(fac[i],mod - 2);
    }
    cin >> n >> l;
    for(int i = 1;i <= n;i++)
    {
        cin >> r[i];
    }
    sort(r + 1,r + n + 1);
    dp[0][0][0] = 1;
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j <= i;j++)
        {
            for(int k = 0;k < l;k++)
            {
                if(k + r[i + 1] <= l)//插入在一个连续段的两端
                {
                    dp[i + 1][j][k + r[i + 1]] = (dp[i + 1][j][k + r[i + 1]] + dp[i][j][k] * j * 2 % mod) % mod;
                }
                if(k + 2 * r[i + 1] - 1 <= l && j >= 2)//合并两个新段
                {
                    dp[i + 1][j - 1][k + 2 * r[i + 1] - 1] = (dp[i + 1][j - 1][k + 2 * r[i + 1] - 1] + dp[i][j][k] * (j - 1) % mod) % mod;
                }
                if(k + 1 <= l)
                {
                    dp[i + 1][j + 1][k + 1] = (dp[i + 1][j + 1][k + 1] + dp[i][j][k] * (j + 1) % mod) % mod;//增加一个段
                }
            }
        }
    }
    for(int i = 0;i <= l;i++)
    {
        g[i] = dp[n][1][i];
    }
    int ans = 0;
    for(int i = 0;i <= l;i++)
    {
        ans = (ans + C(l - i + n,n) * g[i] % mod) % mod;
    }
    cout << ans;
    return 0;
}