机器学习-无监督机器学习-主成分分析PCA-23
1. 降维的方式
对于维度灾难、数据冗余,这些在数据处理中常见的场景,我们不得不进一步处理,得到更精简更有价值的特征信息,所用的的各种方法的统称就是降维
特征抽取:叫做特征映射更合适。因为它的思想即把高维空间的数据映射到低维空间。各种方法包括:
Principal Component Analysis (PCA)
Linear Discriminant Analysis (LDA)
特征选择:试图找到原始特征集合的子集,也就是只选取部分特征
什么是卡方检验Chi-Square test [kai]
用于检测数据集里面的最佳特征,测定哪些特征是输出类别最依赖的, 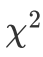
值越高,输出标签越依赖这个特征,并且这个特征有更高的重要性来决定输出值。
假设:有m个特征值并且有k个输出标签
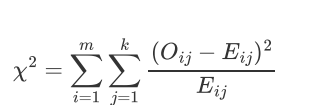
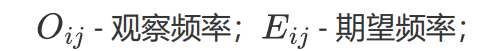
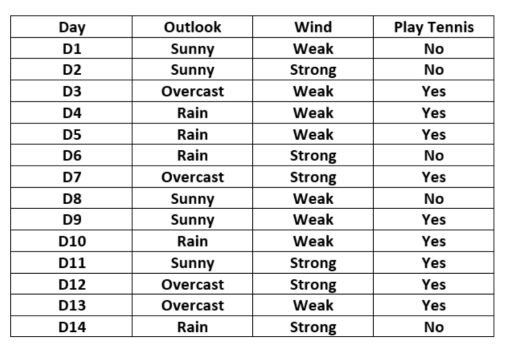
outlook wind两个维度 决定是否play tennis
对于"Outlook"特征可以构建下表:
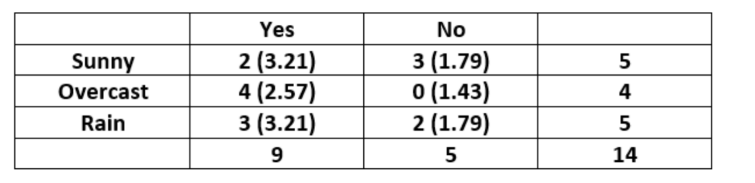
单元格(Sunny,Yes)的期望值计算: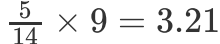
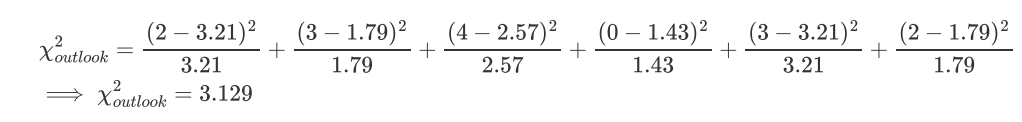
对于"Wind"特征可以构建下表:
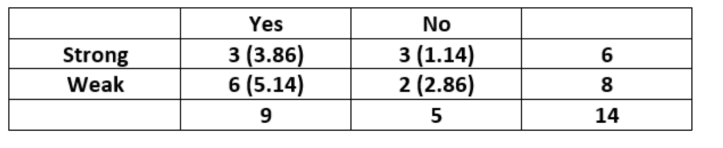

"Wind"是更重要的特征去决定输出值
2. PCA的一般步骤
常用的线性方法是主成分分析PCA。它的思想就是将数据从高维空间映射到低维空间,同时在低维空间里数据的方差被最大化。维度下降 但是最大的保持信息量

留下来少量的特征向量,所以或许这个过程有一些数据丢失。但是最重要的方差应该被保留在了这些特征向量中。
用2维降到1维来举例,
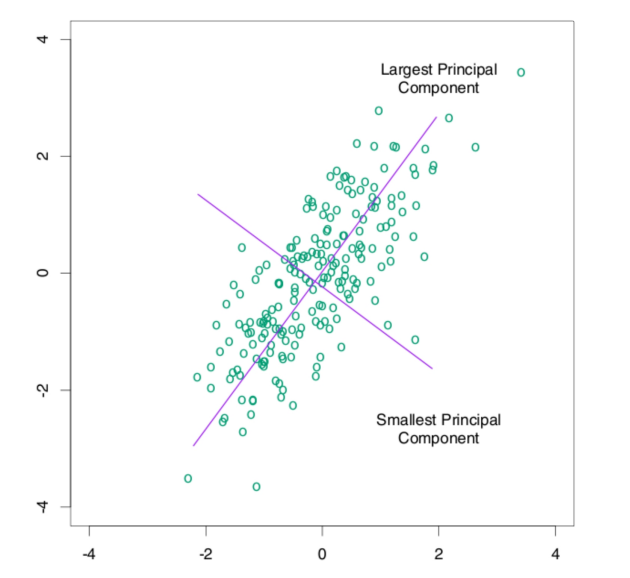
将到1维后 肯定选择方差更大的维度去记录特征 对于变化不大的特征 信息量就少
数据进行降维 本质上观测的对象是不会变化的 只是换一个不同的角度 用新的维度去描述被观察的对象
样本点投影到新的坐标轴

W是变换矩阵
x是所有的样本集
把所有的样本点投影到w1方向 使得投影后的点方差最大,
新坐标系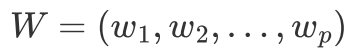
p个维度,设置成标准正交基:
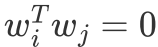
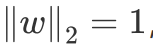
方差的计算:
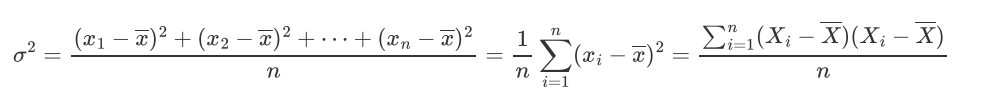
投影之后:
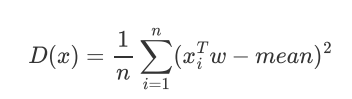
注意点:
PCA会对未投影前的原始数据进行标准归一化,均值归一化也叫中心化:好处是上式中的mean也会为0,推导如下;
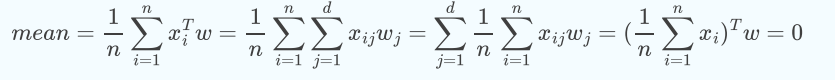
也就是PCA之前 样本数据已经全部移到了(0,0)原点
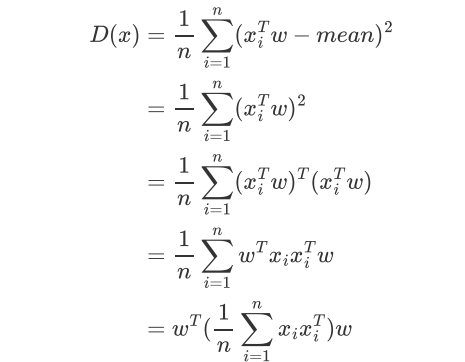
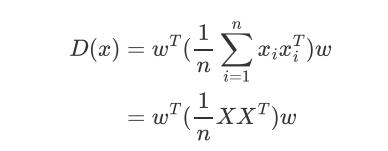
协方差公式:
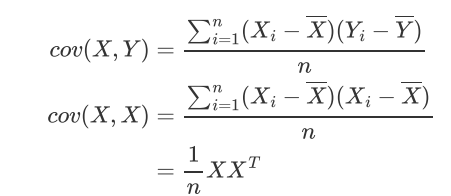
协方差矩阵用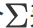 表示
表示
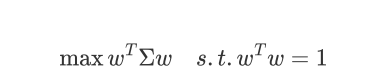
拉格朗日函数:

对w求导
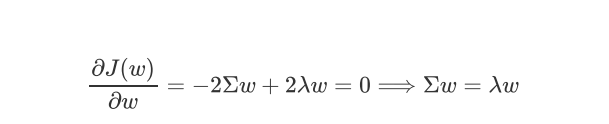
w是sigma的特征向量,lamda是对应的特征值

我们要去寻找的第一主成分,就是使得投影方差最大的坐标轴就是最大特征值对应的特征向量
最终想要保留下来几个维度,我们就选取前几个最大的特征值对应的特征向量,然后把原始的数据在这些轴上面进行投影即可
比如取前 个大的特征值对应的特征向量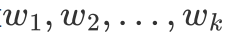
通过以下映射将d维样本映射到k维
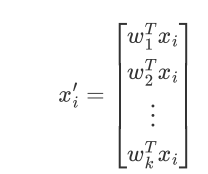
降维后的信息占比:
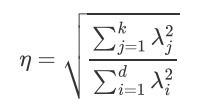
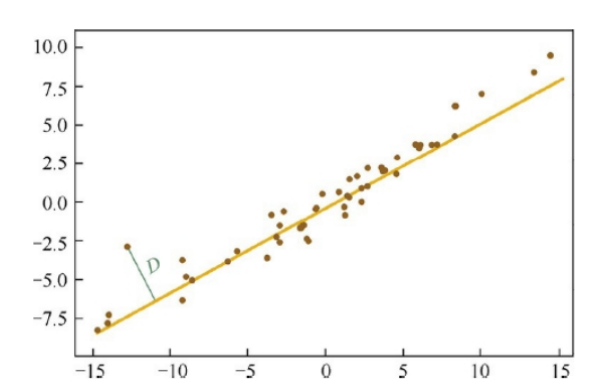
3. 思想2 最小化投影距离
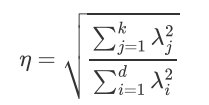
但是这个和线性回归还是有区别 线性回归 y-y_hat 最小,这里是求距离
wi 与xk 都是d维的向量
xk在各个维度投影后加和得到 投影后的点位置:
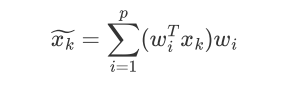
目标转换成:
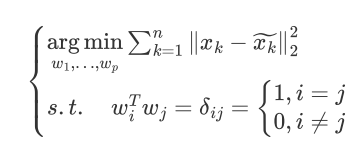
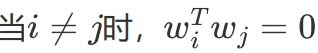
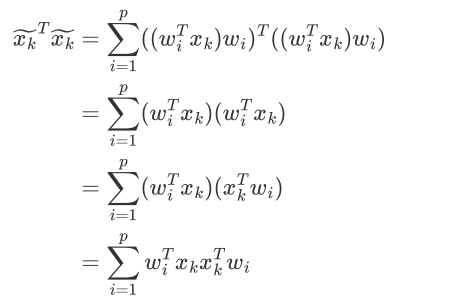

再使用同样的步骤就可以求得最终的投影空间,最佳投影方向就是最大特征值所对应的特征向量。
4. Kernelized PCA
有时我们的数据并不是可以投影到线性超平面的,这时候就不能直接进行PCA降维
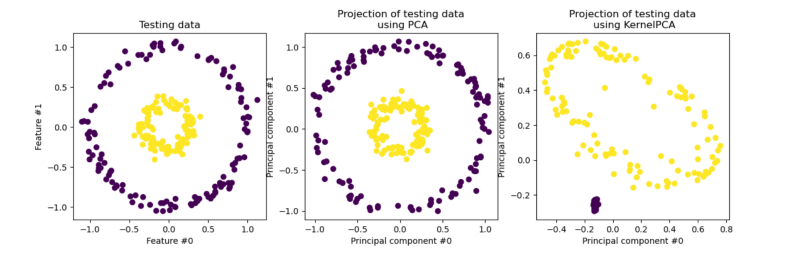
先把数据从n维映射到线性可分的高维N>n,然后再从N维降维到一个低维度n',这里的维度之间满足n' < n < N
映射函数φ将n维映射到N维:
N维:
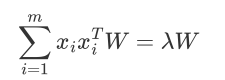
映射为:
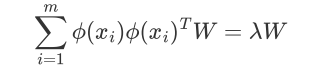
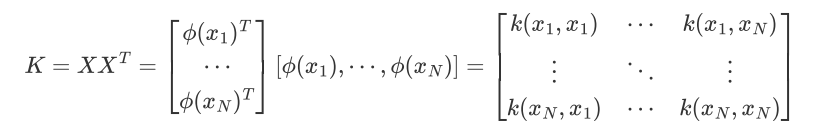
机器学习-无监督机器学习-主成分分析PCA-23的更多相关文章
- 无监督LDA、PCA、k-means三种方法之间的的联系及推导
\(LDA\)是一种比较常见的有监督分类方法,常用于降维和分类任务中:而\(PCA\)是一种无监督降维技术:\(k\)-means则是一种在聚类任务中应用非常广泛的数据预处理方法. 本文的 ...
- 深度学习——无监督,自动编码器——尽管自动编码器与 PCA 很相似,but自动编码器既能表征线性变换,也能表征非线性变换;而 PCA 只能执行线性变换
自动编码器是一种有三层的神经网络:输入层.隐藏层(编码层)和解码层.该网络的目的是重构其输入,使其隐藏层学习到该输入的良好表征. 自动编码器神经网络是一种无监督机器学习算法,其应用了反向传播,可将目标 ...
- 学习笔记CB008:词义消歧、有监督、无监督、语义角色标注、信息检索、TF-IDF、隐含语义索引模型
词义消歧,句子.篇章语义理解基础,必须解决.语言都有大量多种含义词汇.词义消歧,可通过机器学习方法解决.词义消歧有监督机器学习分类算法,判断词义所属分类.词义消歧无监督机器学习聚类算法,把词义聚成多类 ...
- 1(1).有监督 VS 无监督
对比一 : 有标签 vs 无标签 有监督机器学习又被称为“有老师的学习”,所谓的老师就是标签.有监督的过程为先通过已知的训练样本(如已知输入和对应的输出)来训练,从而得到一个最优模型,再将这个模型应用 ...
- 主成分分析(PCA)与线性判别分析(LDA)
主成分分析 线性.非监督.全局的降维算法 PCA最大方差理论 出发点:在信号处理领域,信号具有较大方差,噪声具有较小方差 目标:最大化投影方差,让数据在主投影方向上方差最大 PCA的求解方法: 对样本 ...
- 机器学习 —— 基础整理(四)特征提取之线性方法:主成分分析PCA、独立成分分析ICA、线性判别分析LDA
本文简单整理了以下内容: (一)维数灾难 (二)特征提取--线性方法 1. 主成分分析PCA 2. 独立成分分析ICA 3. 线性判别分析LDA (一)维数灾难(Curse of dimensiona ...
- darktrace 亮点是使用的无监督学习(贝叶斯网络、聚类、递归贝叶斯估计)发现未知威胁——使用无人监督 机器学习反而允许系统发现罕见的和以前看不见的威胁,这些威胁本身并不依赖 不完善的训练数据集。 学习正常数据,发现异常!
先说说他们的产品:企业免疫系统(基于异常发现来识别威胁) 可以看到是面向企业内部安全的! 优点整个网络拓扑的三维可视化企业威胁级别的实时全局概述智能地聚类异常泛频谱观测 - 高阶网络拓扑;特定群集,子 ...
- 机器学习之主成分分析PCA原理笔记
1. 相关背景 在许多领域的研究与应用中,通常需要对含有多个变量的数据进行观测,收集大量数据后进行分析寻找规律.多变量大数据集无疑会为研究和应用提供丰富的信息,但是也在一定程度上增加了数据采集的 ...
- 机器学习降维方法概括, LASSO参数缩减、主成分分析PCA、小波分析、线性判别LDA、拉普拉斯映射、深度学习SparseAutoEncoder、矩阵奇异值分解SVD、LLE局部线性嵌入、Isomap等距映射
机器学习降维方法概括 版权声明:本文为博主原创文章,未经博主允许不得转载. https://blog.csdn.net/u014772862/article/details/52335970 最近 ...
- 机器学习课程-第8周-降维(Dimensionality Reduction)—主成分分析(PCA)
1. 动机一:数据压缩 第二种类型的 无监督学习问题,称为 降维.有几个不同的的原因使你可能想要做降维.一是数据压缩,数据压缩不仅允许我们压缩数据,因而使用较少的计算机内存或磁盘空间,但它也让我们加快 ...
随机推荐
- Chrome扩展的核心:manifest 文件(中)
大家好,我是 dom 哥.我正在写关于 Chrome 扩展开发的系列文章,感兴趣的可以 点个小星星 . 在上一篇中已经完成了 Chrome 扩展的雏形,本篇接着介绍 manifest 中的可选字段,完 ...
- 生成式AI:未来的发展方向是什么?
生成式AI的问世标志着人工智能领域迎来了一个全新时代的开启.今年,ChatGPT的面世引起了广泛的热议和关注,许多人认为这标志着人工智能领域进入了一个大规模探索的时代.然而,事实上,这只是生成式AI发 ...
- 腾讯云服务器安装MySQL5.7基于xshell
腾讯云服务器安装MySQL5.7基于xshell 下载MySQL57安装包 wget https://dev.mysql.com/get/mysql57-community-release-el7-1 ...
- rcs群发软件系统功能设计与应用,rcs群发软件系统,rcs群发软件
随着科技的不断发展,人们对于通讯方式的需求也在不断变化,传统的短信.电话已经无法满足人们对于高效.便捷.实时的通讯需求,正是在这样的背景下,富通讯解决方案(Rich Communication Sui ...
- 春秋云镜 - CVE-2022-29464
WSO2文件上传漏洞(CVE-2022-29464)是Orange Tsai发现的WSO2上的严重漏洞.该漏洞是一种未经身份验证的无限制任意文件上传,允许未经身份验证的攻击者通过上传恶意JSP文件在W ...
- MySQL|MySQL事物以及隔离级别
MySQL 事务主要用于处理操作量大,复杂度高的数据.比如开单,需要添加给订单表增加记录,还需要增加订单的各种相关明细,操作复杂度高,这些操作语句需要构成一个事务.在 MySQL 命令行的默认设置下, ...
- 太赞了!墙裂推荐这款网页版 Nginx 配置生成器,好用到爆!
之前民工哥也给大家介绍过一款Nginx配置生成器:强大!Nginx 配置在线一键生成"神器",不太了解的人可以去看一看. 最近民工哥又发现一款好用的网页版开源工具,同样它的功能也是 ...
- STM32CubeMX教程8 TIM 通用定时器 - 输出比较
1.准备材料 开发板(STM32F407G-DISC1) ST-LINK/V2驱动 STM32CubeMX软件(Version 6.10.0) keil µVision5 IDE(MDK-Arm) 逻 ...
- Cesium案例解析(十)——CZML点
目录 1. 概述 2. 案例 3. 结果 1. 概述 CZML是Cesium中用于描述动态图形场景的JSON格式,它们的关系类似于Google Earth与KML之间的关系,一般会认为KML是一种矢量 ...
- FQS:一种神奇的数仓查询优化技术
本文分享自华为云社区<根据执行计划优化SQL[绽放吧!GaussDB(DWS)云原生数仓]>,作者:西岭雪山. 引言 如果您刚接触DWS那一定会好奇想要知道"REMOTE_FQS ...
