【LCA 树上两点的距离 判定点是否在某条边中】洛谷P3398 仓鼠找sugar

题目链接:P3398 仓鼠找 sugar - 洛谷 | (luogu.com.cn)

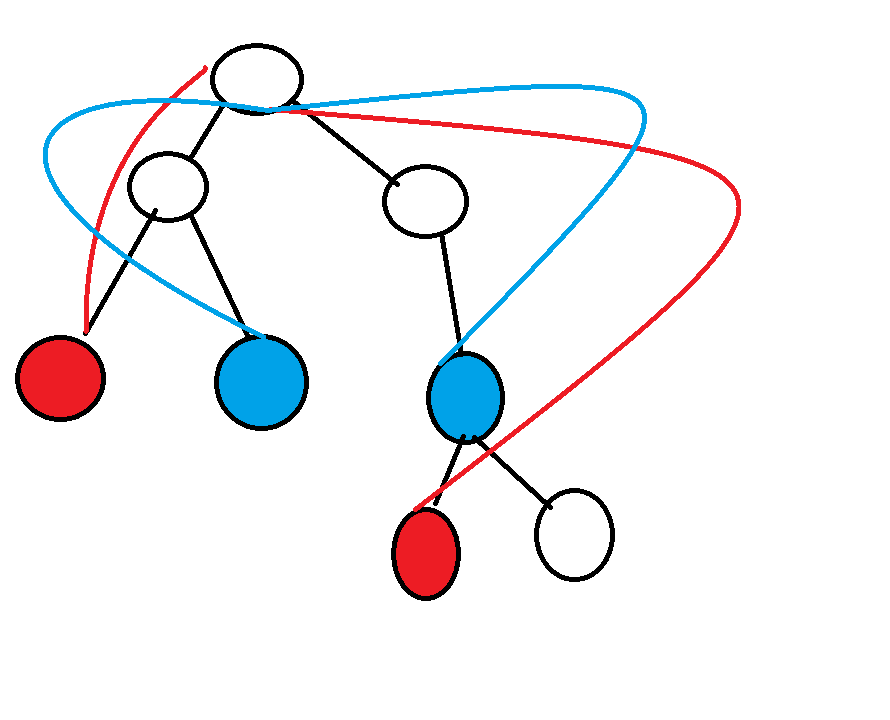
题目大意:判定一棵树上的两条边是否相交

Tag:

[LCA] [树上两点间距离的计算] [如何判断与点在某条路径上]

思路:

\[\begin{align}
&1.建图\\
&2.\text{dfs}然后\ 计算出每个点的深度 和计\text{anc}(i,j)\\
&3.根据树上路径唯一的性质 \quad 如果一个点在某条边上\\
&那么u到边的两端点的距离\text{dis}(a,b) = \text{dis}(a,u)+\text{dis}(u,b)\\
&\text{dis}(a,b) = \text{depth}(a)+\text{depth}(b)-2\times\text{depth}(c)\\
& 其中c=\text{LCA}(a,b)

\end{align}
\]

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=2e5+9;
const int LOG = log2(N)+1;
int idx=0,head[N];
struct node{
    int to,val,next;
};
node e[N<<1];
bool vis[N];
int fa[N];
int anc[N][LOG];
int depth[N];
int n,Q;
int logn;
void add(int u,int v,int val){
    e[idx] = {v,val,head[u]};
    head[u] = idx++;
}
void bd(){
    cin>>n>>Q;
    logn = log2(n);
    memset(head,-1,sizeof(head));
    for(int i=1 ; i<=n-1 ; ++i){
        int u,v;
        cin>>u>>v;
        add(v,u,0);
        add(u,v,0);
    }
}
void dfs(int u,int fa){
    anc[u][0]=fa;
    for(int i=head[u] ; i!=-1 ; i=e[i].next){
        int v = e[i].to;
        if(v==fa) continue;
        depth[v] = depth[u] +1;
        dfs(v,u);
    }
}
void init(){
    for(int j=1 ; j<=logn ;++j){
        for(int i=1 ; i<=n; ++i){
            int v = anc[i][j-1];
            anc[i][j] = anc[v][j-1];
        }
    }
}
int LCA(int u,int v){
    if(u==v) return u;
    if(depth[v] > depth[u])
        swap(u,v);
    for(int i=logn ; i>=0; --i){
        if( depth[u] -(1<<i) >= depth[v])
            u =anc[u][i];
    }
    if(u == v) return u;

    for(int i=logn ; i>=0; --i){
        if(anc[u][i] != anc[v][i] ){
            u = anc[u][i];
            v = anc[v][i];
        }
    }
    return anc[u][0];
}
bool check(int a,int b,int c,int d){
    if(a==c || a==d || b==c || b==d ) return true;
    return false;
}
int dis(int a,int b){
    int c = LCA(a,b);
    return depth[a]+depth[b]-2*depth[c];
    //return abs(depth[a]-depth[c])+abs(depth[b]-depth[c]);
}
int main(){
    bd();
    dfs(1,0);
    init();
    for(int i=1 ; i<=Q ; ++i){
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        if(check(a,b,c,d)) cout<<"Y"<<"\n";
        else {
            int len1 = dis(a,b);
            int len2 = dis(c,d);
            int join1 = LCA(a,b);
            int join2 = LCA(c,d);
            if( ( dis(a,join2) + dis(b,join2) ==len1 ) || ( dis(d,join1) + dis(c,join1) ==len2) )
                cout << "Y" << "\n";
            else
                cout << "N" << "\n"; // 确保输出结果
        }
    }
}