Solution Set -「ARC 109」

「ARC 109A」Hands

Link.

讨论即可，除了煞笔出题人写了个死马的题面。

#include<cstdio>
#include<algorithm>
using namespace std;
int a,b,x,y,ans;
int main()
{
	scanf("%d%d%d%d",&a,&b,&x,&y);
	if(a>b)	printf("%d\n",min(x<<1,y)*max(0,abs(a-b)-1)+x);
	else	printf("%d\n",min(x<<1,y)*max(0,abs(a-b))+x);
	return 0;
}

「ARC 109B」log

Link.

要贪心的取的话，肯定是先把 \(n+1\) 取了，然后我们来二分。

\(1-n\) 分别有 \(n+1\) 到 \(2\) 种方法可以组成他。

然后来考虑怎么 check。

可以知晓，如果没有这一块多的木块，就一定需要 \(n\) 块木头。

然后就按开头那个贪心，把 \(n+1\) 从 \(1\) 分完，剩下的再依次分。

#include<cstdio>
unsigned long long n;
bool check(unsigned long long x)
{
	return (x*(x+1)>>1)<=n+1;
}
unsigned long long search(unsigned long long l,unsigned long long r)
{
	unsigned long long res=0;
	while(l<=r)
	{
		unsigned long long mid=(l+r)>>1;
		if(check(mid))
		{
			l=mid+1;
			res=n-mid+1;
		}
		else	r=mid-1;
	}
	return res;
}
int main()
{
	scanf("%llu",&n);
	printf("%llu\n",search(1,2e9));
	return 0;
}

「ARC 109C」Large RPS Tournament

Link.

\(2^{k}\)！好耶！！！

考虑倍增 DP。设 \(f_{i,j}\) 为区间 \([i,i+2^{j}-1]\) 的 winner's hand。

设计一个函数 \(\text{tournament}(P,Q)\) 为 \(P\)、\(Q\) 比武后的赢家。

转移即

\[f_{i,j}=\text{tournament}(f_{i,j-1},f_{i+2^{j-1},j-1})
\]

当然你不能直接用 \(2^{k}\) 当成序列来做，反正他是循环节我们直接做 \(k\) 轮最后合并即可。

实际实现时不需要这么写（主要是写不来）（好像可以记忆化？）。

#include<string>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
string s;
int n,k;
char tour(char one,char ano)
{
	if(one=='R')
	{
		if(ano=='R')	return 'R';
		else if(ano=='P')	return 'P';
		else	return 'R';
	}
	else if(one=='P')
	{
		if(ano=='R')	return 'P';
		else if(ano=='P')	return 'P';
		else	return 'S';
	}
	else
	{
		if(ano=='R')	return 'R';
		else if(ano=='P')	return 'S';
		else	return 'S';
	}
}
int main()
{
	scanf("%d%d",&n,&k);
	cin>>s;
	while(k--)
	{
		string tmp=s+s;
		for(int i=0;i<n;++i)	s[i]=tour(tmp[i<<1],tmp[i<<1|1]);
	}
	printf("%c\n",s[0]);
	return 0;
}

「ARC 109D」L

图画出来差不多，向目标进发，步数下界就出来了 \(\max\{|x|,|y|\}\)。

这张图是在这里嫖的：

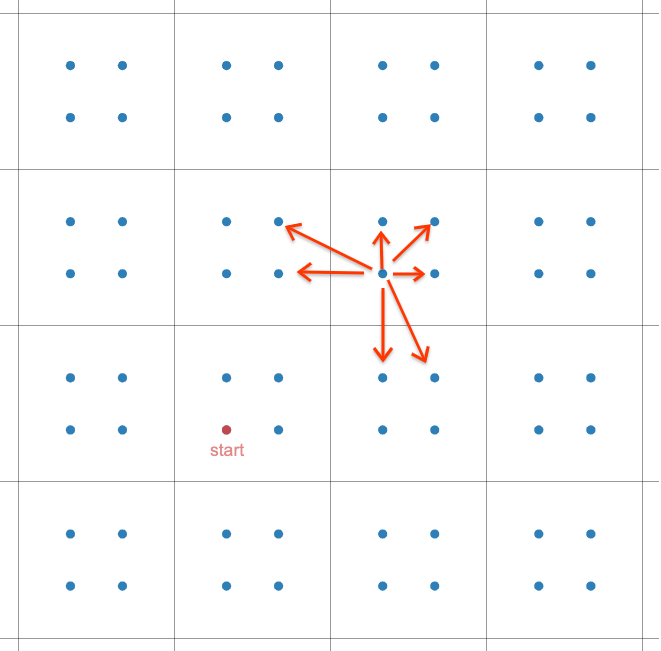
注意特判一些奇怪的情况，具体自己看代码吧吧吧吧。

#include<cstdio>
#include<algorithm>
using namespace std;
int t,onex,oney,anox,anoy,exx,exy,finalx,finaly;
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d%d%d%d%d",&onex,&oney,&anox,&anoy,&exx,&exy);
		finalx=min(onex,min(anox,exx));
		finaly=min(oney,min(anoy,exy));
		finalx=(finalx<<1)+(finalx!=onex)+(finalx!=anox)+(finalx!=exx)-1;
		finaly=(finaly<<1)+(finaly!=oney)+(finaly!=anoy)+(finaly!=exy)-1;
		printf("%d\n",max(abs(finalx),abs(finaly))+((finalx==finaly)&&(finalx>1||finalx<0)));
	}
	return 0;
}

「ARC 109E」1D Reversi Builder

Link.

「ARC 109F」1D Kingdom Builder

Link.