洛谷 pP2146 [NOI2015]软件包管理器

题目的传送门

题目描述

Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。Debian/Ubuntu使用的apt-get，Fedora/CentOS使用的yum，以及OSX下可用的homebrew都是优秀的软件包管理器。

你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包A依赖软件包B，那么安装软件包A以前，必须先安装软件包B。同时，如果想要卸载软件包B，则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除0号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而0号软件包不依赖任何一个软件包。依赖关系不存在环（若有m(m≥2)个软件包A1,A2,A3,⋯,Am，其中A1依赖A2，A2依赖A3，A3依赖A4，……，A[m-1]依赖Am，而Am依赖A1，则称这m个软件包的依赖关系构成环），当然也不会有一个软件包依赖自己。

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为0。

输入输出格式

输入格式：

从文件manager.in中读入数据。

输入文件的第1行包含1个整数n，表示软件包的总数。软件包从0开始编号。

随后一行包含n−1个整数，相邻整数之间用单个空格隔开，分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。

接下来一行包含1个整数q，表示询问的总数。之后q行，每行1个询问。询问分为两种：

install x：表示安装软件包x

uninstall x：表示卸载软件包x

你需要维护每个软件包的安装状态，一开始所有的软件包都处于未安装状态。

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

输出格式：

输出到文件manager.out中。

输出文件包括q行。

输出文件的第i行输出1个整数，为第i步操作中改变安装状态的软件包数。

输入输出样例

输入样例#1： 复制

7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0

输出样例#1： 复制

3
1
3
2
3

输入样例#2： 复制

10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9

输出样例#2： 复制

1
3
2
1
3
1
1
1
0
1

说明

【样例说明 1】

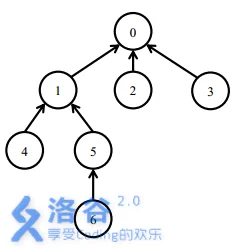
一开始所有的软件包都处于未安装状态。

安装5号软件包，需要安装0,1,5三个软件包。

之后安装6号软件包，只需要安装6号软件包。此时安装了0,1,5,6四个软件包。

卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。

之后安装4号软件包，需要安装1,4两个软件包。此时0,1,4处在安装状态。最后，卸载0号软件包会卸载所有的软件包。`

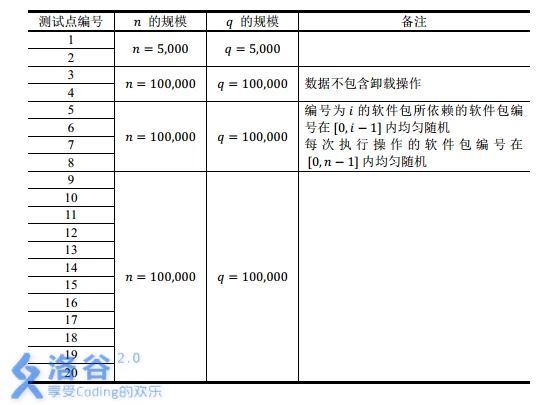
【数据范围】

思路：

这题最难的应该在读题，一遍题目读下来都不知道在说什么。。。。

对于本题，有两个操作：

1. install x ：表示要安装软件包x;
2. uninstall x ：表示要卸载此安装包；

对于操作一，可以统计从x节点到根节点还未安装软件包的节点数，然后用区间改改成已安装。

对于操作二，可以先统计x所在的子树中已安装的节点数，然后将子树改为没安装。

其他的真的没什么，跟板子也没什么区别，只是注意别超时了，就像我原来的DFS1就写丑了，然后一堆T

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>

 using namespace std;

 const int maxn=5e6+;
 struct node
 {
     int to,next;
 }way[maxn];
 struct tttt
 {
     int l,r,ls,rs;
     int sum;
     int lazy;
 }tree[maxn];
 int top[maxn];
 int head[maxn];
 int deep[maxn];
 int size[maxn];
 int dfsx[maxn];
 int rt[maxn];
 int n,m,rt1;
 int son[maxn];
 int tot;
 int father[maxn];

 int read()
 {
     int x=;char ch=getchar();
     while(ch<''||ch>''){ch=getchar();}
     while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x;
 }

 void add(int x,int y)
 {
     way[++tot].next=head[x];
     way[tot].to=y;
     head[x]=tot;
 }

 int len(int x)
 {
     return tree[x].r-tree[x].l+;
 }

 /*void dfs1(int x)
 {
     deep[x]=deep[father[x]]+1;
     size[x]=1;
     for(int i=head[x];i;i=way[i].next)
     {
         int to=way[i].to;
         if(to!=father[x])
         {
             father[to]=x;
             dfs1(to);
             size[x]+=size[to];
             if(size[to]>size[son[x]])
             {
                 son[x]=to;
             }
         }
     }
 }*/

 void dfs1(int u,int fa,int depth)
 {
     father[u]=fa;
     deep[u]=depth;
     size[u]=;
     for(int i=head[u];i;i=way[i].next)
     {
         int to=way[i].to;
         if(to==fa)
             continue;
         dfs1(to,u,depth+);
         size[u]+=size[to];
         if(size[to]>size[son[u]]||!son[u])
             son[u]=to;
     }
 }
 int dfs2(int x,int t)
 {
     top[x]=t;
     dfsx[x]=++tot;
     rt[tot]=x;
     if(son[x])
     {
         dfs2(son[x],t);
     }
     for(int i=head[x];i;i=way[i].next)
     {
         int to=way[i].to;
         if(to!=father[x]&&to!=son[x])
         {
             dfs2(to,to);
         }
     }
 }

 int pushup(int x)
 {
     tree[x].sum=tree[tree[x].rs].sum+tree[tree[x].ls].sum;
     tree[x].l=tree[tree[x].ls].l;
     tree[x].r=tree[tree[x].rs].r;
 }

 void build (int l,int r,int x)
 {
     if(l==r)
     {
         tree[x].ls=tree[x].rs=tree[x].lazy=-;
         tree[x].l=tree[x].r=l;
         return ;
     }
     int mid=(l+r)>>;
     tree[x].ls=tot++;
     tree[x].rs=tot++;
     build(l,mid,tree[x].ls);
     build(mid+,r,tree[x].rs);
     pushup(x);
 }

 int pushdown(int x)
 {
     int ls=tree[x].ls;
     int rs=tree[x].rs;
     int lz=tree[x].lazy;
     tree[ls].sum=lz*len(ls);
     tree[rs].sum=lz*len(rs);
     tree[ls].lazy=tree[x].lazy;
     tree[rs].lazy=tree[x].lazy;
     tree[x].lazy=-;
 }

 void update(int l,int r,int c,int x)
 {
     if(tree[x].l>=l&&tree[x].r<=r)
     {
         tree[x].lazy=c;
         tree[x].sum=c*len(x);
         return ;
     }
     if(tree[x].lazy!=-)
     pushdown(x);
     int mid=(tree[x].l+tree[x].r)>>;
     if(mid>=l)
     {
         update(l,r,c,tree[x].ls);
     }
     if(mid<r)
     {
         update(l,r,c,tree[x].rs);
     }
     pushup(x);
 }

 int qwery(int l,int r,int x)
 {
     if(tree[x].l>=l&&tree[x].r<=r)
     {
         return tree[x].sum;
     }
     if(tree[x].lazy!=-)
     {
         pushdown(x);
     }
     int mid=(tree[x].l+tree[x].r)>>;
     int res=;
     if(mid>=l)
     {
         res+=qwery(l,r,tree[x].ls);
     }
     if(mid<r)
     {
         res+=qwery(l,r,tree[x].rs);
     }
     return res;
 }

 int ask(int x)
 {
     int ans=;
     while(top[x])
     {
         ans+=dfsx[x]-dfsx[top[x]]-qwery(dfsx[top[x]],dfsx[x],rt1)+;
         update(dfsx[top[x]],dfsx[x],,rt1);
         x=father[top[x]];
     }
     ans+=dfsx[x]-dfsx[]-qwery(dfsx[],dfsx[x],rt1)+;
     update(dfsx[],dfsx[x],,rt1);
     return ans;
 }

 int main()
 {
     n=read();
     for(int i=;i<n;i++)
     {
         int x;
         x=read();
         add(x,i);
         add(i,x);
     }
     tot=;
     dfs1(,-,);
     dfs2(,);
     tot=;
     rt1=tot++;
     build(,n,rt1);
     m=read();
     for(int i=;i<=m;i++)
     {
         string flag;
         cin>>flag;
         int op;
         op=read();
         if(flag=="install")
         {
             printf("%d\n",ask(op));
         }
         else
         if(flag=="uninstall")
         {
             int ans=qwery(dfsx[op],dfsx[op]+size[op]-,rt1);
             printf("%d\n",ans);
             update(dfsx[op],dfsx[op]+size[op]-,,rt1);
         }
     }
     return ;
  }