线性代数笔记24——微分方程和exp(At)

　　原文：https://mp.weixin.qq.com/s/COpYKxQDMhqJRuMK2raMKQ

　　微分方程指含有未知函数及其导数的关系式，解微分方程就是找出未知函数。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的，叫做偏微分方程。常微分方程有时也简称方程。微分方程是一门复杂的学科，对于常微分方程来说，可以使用特征值和特征向量的知识求解。

　

　　相关前置知识：

　　　　微分方程：单变量微积分11——常微分方程和分离变量

　　　　泰勒公式：单变量微积分30——幂级数和泰勒级数

　　　　泰勒公式在0点展开的原因：多项式函数能够拟合非线性问题原理

　　　　求逆矩阵：线性代数笔记8——求解逆矩阵

　　　　求行列式：线性代数20——行列式和代数余子式

　　　　特征值和特征向量：线性代数22——特征值和特征向量

　　　   矩阵对角化：线性代数笔记23——矩阵的对角化和方幂

常微分方程的一般解法

　　根据概念构造一个常微分方程：

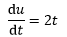
　　目标是求得原函数u=u(t)的具体形式。通过积分求解：

　　这就是最终答案的通解，C是任意常数。实际上这种解法就是利用了不定积分的知识：

　　

　　如果du/dt=u，可以使用分离变量法的求解方式：

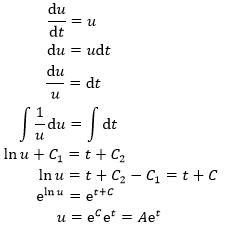
　　也就是说，当函数的导数是函数本身的时候，这个函数就是型如Ae^t的函数，由于A=e^C是任意常数，所以经常用C代替A，写成u=Ce^t的形式。

　　同理，对于du/dt=λu，微分方程的解是u(t)=Ce^λt。当t=0时：

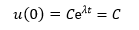
　　由于C是任意常数，因此可以取C=u(0)，得到u(t)= u(0)e^λt，这样做可以去掉常数C。在实际问题中，u可以表示关于时间t的函数，对于时间来说，通常可以把t=0看作初始条件。

常微分方程与矩阵

　　现在将常微分方程扩展为常微分方程组，u₁=u₁(t)，u₂=u₂(t)，初始条件是t=0，初始值是u(0)=(1,0)，求解微分方程：

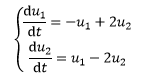
　　可以把微分方程组写成向量矩阵的形式：

　　相当于将常微分方程中转换成了du/dt = Au的线性形式。

常微分方程的线性代数解法

　　对于du/dt = Au来说，u₁和u₂之间存在耦合（没有耦合就没必要写成方程组了），A表示它们的耦合关系：

　　A可以用特征值和特征向量对角化，因此方程的解和矩阵A的特征值和特征向量存在关联关系。先求矩阵A的特征值。

　　或许你可以马上看出A是个奇异矩阵，因此一个特征值是λ₁=0。特征值之和是矩阵的迹，迹是矩阵主对角线元素和，因此可以求得另一个特征值是λ₂=(-1-2)-0=-3。

　　当然也可以用正统的方法求解：

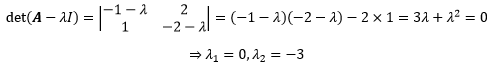
　　接下来根据特征方程求得特征向量。

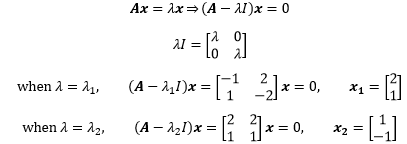
特解

　　微分方程组有两组特解：

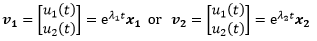
　　这是两个纯指数解的组合。需要注意的是，这里x₁和x₂都是二维向量，因此v₁和v₂也是二维的。

　　来验证一下v₁，如果u=v₁是方程的解，把v₁代入原方程：

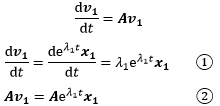
　　只要验证①=②是否成立就可以了，假设等式成立：

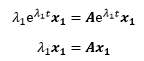
　　x₁和λ₁是Ax=λx的一组特征向量和特征值，因此①=②成立，v₁是微分方程的解。同理，v₂也是微分方程的解。

通解

　　对于du/dt = Au来说，如果v₁和v₂是方程的解，那么它们的线性组合也是方程的解，因此微分方程的通解是：

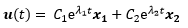
　　验证的方法和验证特解类似：

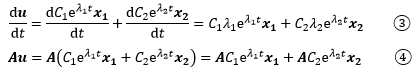
　　只要验证③=④是否成立就可以了，假设等式成立：

　　x₁和λ₁是Ax=λx的一组特征向量和特征值，因此⑤成立。同理，⑥也成立，因此通解成立。

　　最后将λ和x的值代入通解：

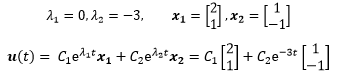
　　如果没有初始条件，到这里就结束了，这就是u(t)的形态。本例给出了初始值，可以由此继续计算出C₁和C₂：

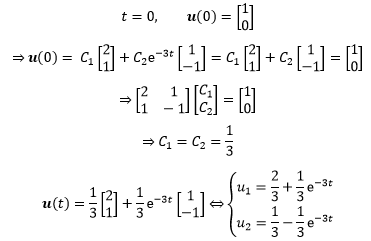
　　当t→∞时：

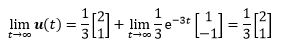
　　随着t的增加，u(t)逐渐收敛到一个定值，我们称u(t)为稳态。

　　通解指出了当A是2×2矩阵时u(t)达到稳态的条件：A的其中一个特征值是0，且另一个特征值小于0（如果是复数，则复数的实部小于0）。如果λ₁=0, λ₂>0，u(t)是发散的。

解耦

　　回顾上一节的内容，在通过初始值求解C的时候：

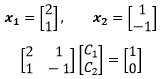
　　如果用S表示特征向量矩阵，则上式可以写成Sc=u(0)，即通过Sc=u(0)可以求得c。

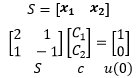
　　常微分方程组du/dt = Au，u=(u₁, u₂)，u₁, u₂是两个互相耦合的未知函数，A表明了它们的耦合关系，求解微分方程组的关键是如何解耦，而解耦的方式正是利用特征值和特征向量。现在的问题是，能否把微分方程的解表示成S和Λ的形式（Λ是特征值矩阵，参考上一章内容）？

　　既然u是通过A耦合的，A又能通过S和Λ对角化（A=SΛS^-1），因此u可以用特征向量矩阵S解耦，令u=Sv，v(t)是某个未知的常微分方程组：

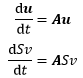
　　S是常矩阵，因此：

　　根据上一章矩阵对角化的内容：

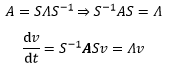
　　这实际上是得到了没有耦合的新方程组：

　　每个方程都可以套用一开始讲过的内容：du/dt=λu，微分方程的解是u(t)=Ce^λt，再代入初始条件t=0，u(t)=u(0)e^λt：

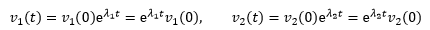
　　将二者合并：

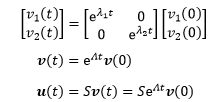
　　v(0)的具体值我们不知道也不关心，只知道是个常向量，Sc=u(0)，c是任意常向量，设c=v(0)：

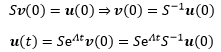
　　更进一步：

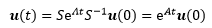
　　接下来解释为什么会得到这个结论。

矩阵指数exp(At)

　　A是矩阵，e^At是以矩阵为指数的表达式，它代表什么意思呢？

　　我们知道f(x)在x=0点处的泰勒展开式：

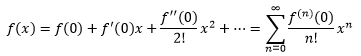
　　e^x在x₀=0点处的泰勒展开式是：

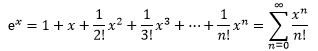
　　0的阶乘是1。展开式是收敛的，越靠后的项对总体的影响越小，越接近于0。证明起来较为容易：

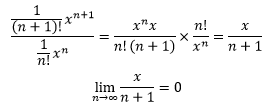
　　因此e^x是收敛的。

　　同样，e^At也在At=O点处进行泰勒展开，注意这里的O是A的同阶零矩阵，e^O等于单位矩阵：

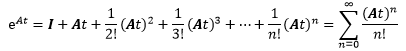
　　e^At也是收敛的。

　　上一章已经讲过矩阵的对角化：

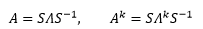
　　代入到e^At中：

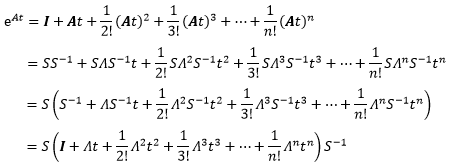
　　中间的一大堆正好是e^∧t的泰勒展开式，因此e^At最终可以写成：

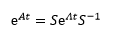
　　这就是矩阵指数的公式，当然，上式成立的前提是A可以对角化，即A_n×n存在n个独立的特征向量。

　　最后再来看看e^∧t是什么。

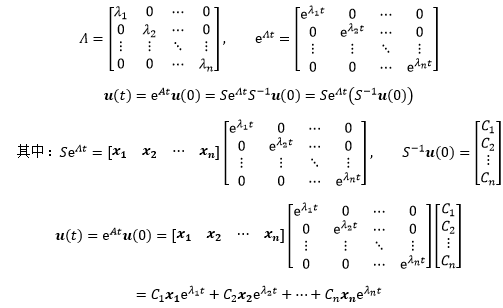
　　和通解的形式一致，如果有初始值，可以根据初始值计算出具体的C。

二阶常微分方程

　　现在有一个二阶常微分方程：

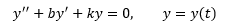
　　求解时需要把方程转换成矩阵的形式：

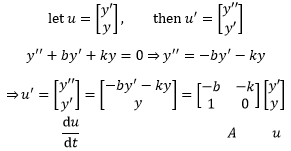
　　这就又变成了du/dt=Au的形式，可以用矩阵直接求解。

综合示例

　　求解三阶常微分方程并构建e^At：

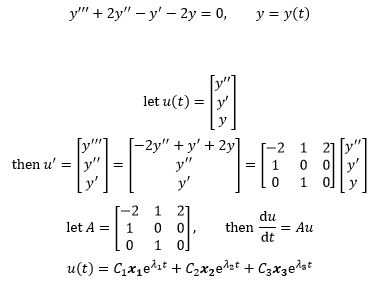
　　接下来需要求得A的特征值和特征矩阵。根据特征方程可得到：

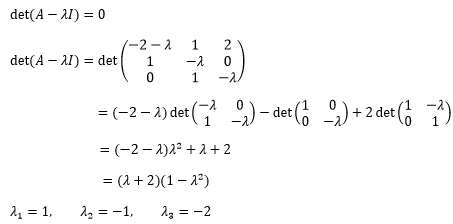
　　接下来通过3个特征值求的特征向量：

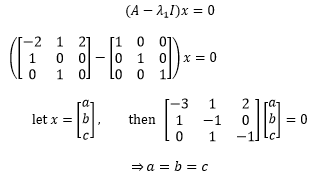
　　第1个特征向量的特解是：

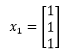
　　类似的方式求得另外两个特征向量：

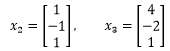
　　u(t)的通解：

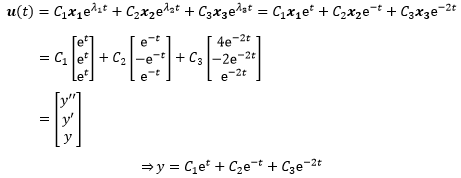
　　最后来构建e^At：

　　

　　

　相关前置知识：

　　　　微分方程：单变量微积分11——常微分方程和分离变量

　　　　泰勒公式：单变量微积分30——幂级数和泰勒级数

　　　　泰勒公式在0点展开的原因：多项式函数能够拟合非线性问题原理

　　　　求逆矩阵：线性代数笔记8——求解逆矩阵

　　　　求行列式：线性代数20——行列式和代数余子式

　　　　特征值和特征向量：线性代数22——特征值和特征向量

　　　   矩阵对角化：线性代数笔记23——矩阵的对角化和方幂

---

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！

　　扫描二维码关注作者公众号“我是8位的”