堆的python实现及其应用

堆的概念

优先队列(priority queue)是一种特殊的队列，取出元素的顺序是按照元素的优先权(关键字)大小，而不是进入队列的顺序，堆就是一种优先队列的实现。堆一般是由数组实现的，逻辑上堆可以被看做一个完全二叉树(除底层元素外是完全充满的，且底层元素是从左到右排列的)。

堆分为最大堆和最小堆，最大堆是指每个根结点的值大于左右孩子的节点值，最小堆则是根结点的值小于左右孩子的值。

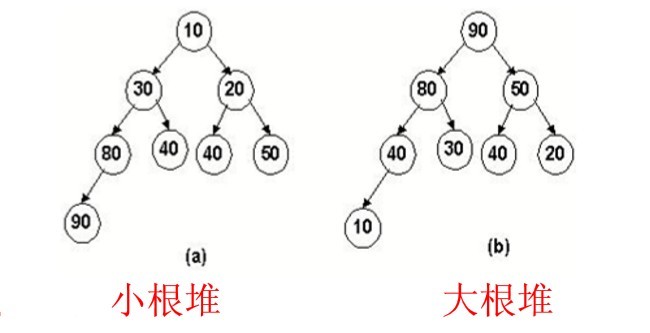
下面就开始用python实现一个小根堆。

最小堆的实现

堆的架构:

堆的核心操作就是插入和删除堆顶元素，除了这些还有一些不常用的其他方法，具体架构如下:

class BinaryHeap(object):
    """一个二叉堆, 小顶堆 利用列表实现"""

    def __init__(self, max_size=math.inf):
        pass

    def __len__(self):
        """求长度"""
        pass

    def insert(self, *data):
        """向堆中插入元素"""
        pass

    def _siftup(self):
        """最后插入的元素上浮"""
        pass

    def _siftdown(self, idx):
        """序号为i的元素下沉"""
        pass

    def get_min(self):
        pass

    def delete_min(self):
        """删除堆顶元素"""
        pass

    def create_heap(self, data):
        """直接创建一个小顶堆, 接收一个可迭代对象参数,效果同insert, 效率比insert一个个插入高,时间复杂度为n"""
        pass

    def clear(self):
        """清空堆"""
        pass

    def update_key(self, idx, key):
        """更新指定位置的元素, idx>=1"""
        pass

    def delete_key(self, idx):
        """删除指定位置的元素, idx>=1"""
        pass

1. 创建空堆对象和求堆的元素数量

下面初始化时默认是一个大小不限的堆，还为列表的0位置创建了一个取值无限小的哨兵，一个是保证插入的值一定比它小，在插入时减少了一次判断，另一个就是让元素下标从1开始。第二个方法实现双下len方法可以统一通过len()查看元素个数。

    def __init__(self, max_size=math.inf):
        self._heap = [-math.inf]             # 初始值设置一个无限大的哨兵
        self.max_size = max_size

    def __len__(self):
        """求长度"""
        return len(self._heap) - 1

2.元素的插入

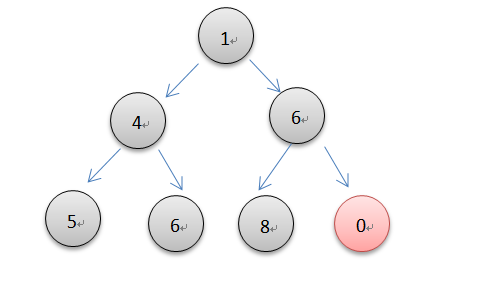
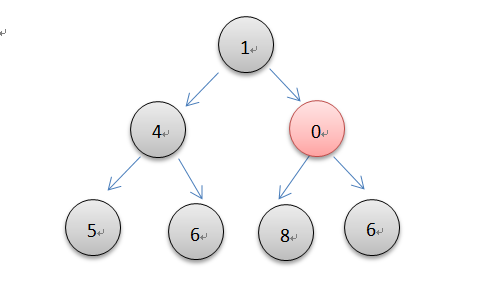
元素的插入，本质就是一个元素上浮的过程。先添加到列表的末尾，然后向上调整插入到合适的位置以维护最小堆的特性。由完全二叉树的性质，根结点序号为1的堆性质是父结点的序号是子节点的1/2，依照如此，代码就很容易写了。下面设置的是可以插入多个元素或是接收一个可迭代对象为参数进行插入。

    def insert(self, *data):
        """向堆中插入元素"""
        if isinstance(data[0], Iterable):
            if len(data) > 1:
                print("插入失败...第一个参数可迭代对象时参数只能有一个")
                return
            data = data[0]
        if not len(self) + len(data) < self.max_size:
            print("堆已满, 插入失败")
            return
        for x in data:
            self._heap.append(x)
            self._siftup()
        print("插入成功")

    def _siftup(self):
        """最后插入的元素上浮"""
        pos = len(self)                     # 插入的位置
        x = self._heap[-1]                  # 获取最后一个位置元素
        while x < self._heap[pos >> 1]:     # 此处可以体现出哨兵的作用了, 当下标为0时, x一定小于inf
            self._heap[pos] = self._heap[pos >> 1]
            pos >>= 1
        self._heap[pos] = x

3. 元素的删除

  

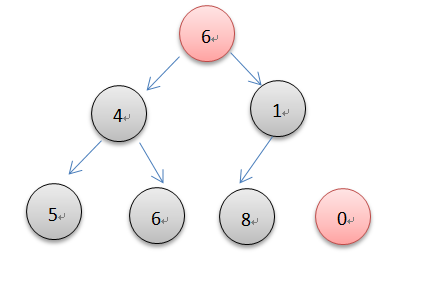
堆顶元素的删除本质就是一个元素下沉的过程。如上图要删除0，先找到最后一个元素，并代替堆顶元素，然后调整其位置。具体过程是左右孩子比大小，然后用堆顶元素和这个小的值比，如果堆顶元素大于小的孩子则用小的孩子代替当前堆顶元素，否则当前位置就是合适的位置。循环以上操作到最后一个元素，也就维护了最小堆的特性。

    def delete_min(self):
        """删除堆顶元素"""
        if not len(self):
            print("堆为空")
            return
        _min = self._heap[1]
        last = self._heap.pop()
        if len(self):               # 为空了就不需要向下了
            self._heap[1] = last
            self._siftdown(1)
        return _min
    def _siftdown(self, idx):
        """序号为i的元素下沉"""
        temp = self._heap[idx]
        length = len(self)
        while 1:
            child_idx = idx << 1
            if child_idx > length:
                break
            if child_idx != length and self._heap[child_idx] > self._heap[child_idx + 1]:
                child_idx += 1
            if temp > self._heap[child_idx]:
                self._heap[idx] = self._heap[child_idx]
            else:
                break
            idx = child_idx
        self._heap[idx] = temp

4. 堆的快速创建

堆的创建可以用上面的insert方法一个一个创建，如此花费的时间是o(nlogn)， 但是也可以直接创建，然后调整堆，最后的时间是o(n)，图示如下所示

　　

　　

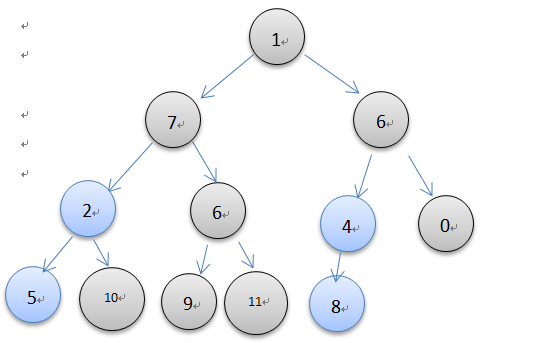
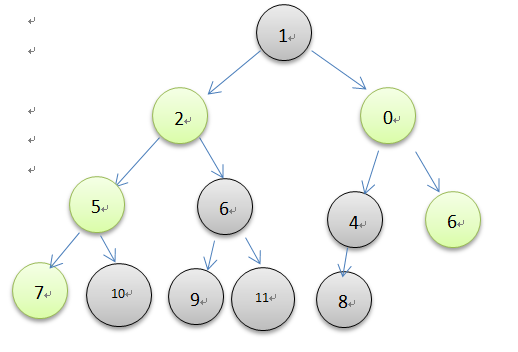
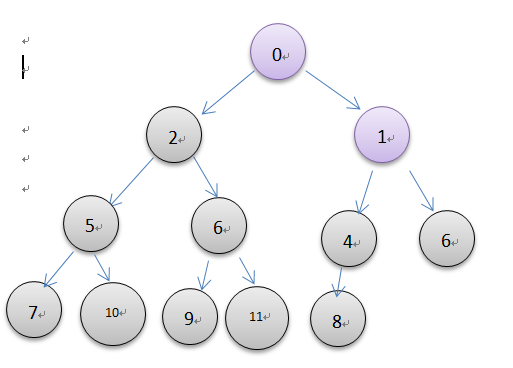
由上图了解可以直接对一个乱序的列表进行调整。当一颗完全二叉树的所有子树都是一个最小堆时，那么这颗树也就是最小堆了。因此从最后一个非叶结点开始调整，叶结点本身就是最小堆，不用调整，可以直接跳过。根据完全二叉树的性质，最后一个非叶结点序号是最后一个元素的序号除以2。在上面的图中，从结点8开始调整，每一次调整就是一次元素的下沉操作，一直到堆顶结束。代码实现很简单，如下所示。

    def create_heap(self, data):
        """直接创建一个小顶堆, 接收一个可迭代对象参数,效果同insert, 效率比insert一个个插入高,时间复杂度为n"""
        self._heap.extend(data)
        for idx in range(len(self) // 2, 0, -1):
            self._siftdown(idx)

5. 堆的其他操作

5.1 获取堆顶元素

    def get_min(self):
        if not len(self):
            print("堆为空")
        return self._heap[1]

5.2 堆的清空

    def clear(self):
        """清空堆"""
        self._heap = [-math.inf]  # 初始值设置一个无限小的哨兵

5.3 更新指定位置的元素

    def update_key(self, idx, key):
        """更新指定位置的元素, idx>=1"""
        if idx > len(self) or idx < 1:
            print("索引超出堆的数量或小于1")
            return
        self._heap[idx] = key
        self._siftdown(idx)

5.4 删除指定位置的元素

    def delete_key(self, idx):
        """删除指定位置的元素, idx>=1"""
        if idx > len(self) or idx < 1:
            print("索引超出堆的数量或小于1")
            return
        x = self._heap.pop()        # 取出最后一个元素代替, 保持完全二叉树, 然后调整到合适位置
        if len(self):
            self._heap[idx] = x
            self._siftdown(idx)

6.堆的应用

6.1 堆排序

堆的应用之一就是堆排序，先把待排序的数据放入堆中，然后一个个删除，整体效率为o(nlogn)

# 堆的应用之一, 堆排序
def heap_sort(data, reverse=False):
    """接受一个可迭代对象进行排序, 默认从小到大排序, 返回一个列表"""
    heap = BinaryHeap()     # 新建一个堆
    heap.create_heap(data)
    lst = []
    for i in range(len(heap)):
        lst.append(heap.delete_min())
    if reverse:
        return lst[::-1]
    return lst

if __name__ == '__main__':print(heap_sort([1, 4, 56, 2, 5, 9, 1, 0, 0, 4], reverse=True))
    print(heap_sort('helloworld'))

输出如下

[56, 9, 5, 4, 4, 2, 1, 1, 0, 0]
['d', 'e', 'h', 'l', 'l', 'l', 'o', 'o', 'r', 'w']

6.2 获取n个数中前k大的数

解决这个问题方法很多，可以利用各种排序算法排序，然后取前k个，下面一个方法运用了最小堆的方法，把问题转化成了从求前k大的数变成了求第k大的数什么的问题。思想就是用前k个数创建一个k大小的最小堆，然后用剩下的数依次去和堆顶比，比堆顶小就舍弃，否则则用刚才的数代替堆顶，然后重新维护更新最小堆。

# 堆的应用之二, 查找n个数中前K大的数, 效率为o(nlogk)
def get_big_nums(data, k):
    """获取前k个最大的数"""
    heap = BinaryHeap(k)
    heap.create_heap(data[:k])  # 用前k个数建立一个小顶堆, 堆顶即是第k大的数

    for d in data[k:]:
        if heap.get_min() < d:
            heap.update_key(1, d)
    lst = []                    # 获取堆里的元素
    for i in range(k):
        lst.append(heap.delete_min())
    return lst

if __name__ == '__main__':
    print(get_big_nums([1, 2, 5, 2, 4, 10, 7, 1, 3, 5, 9], 3))
    print("*" * 30)
    print(get_big_nums([0.1, 2, -1, 89, 67, 13, 55, 54.4, 67], 5))

输出如下

[7, 9, 10]
******************************
[54.4, 55, 67, 67, 89]

下面写一个在编程之美书里介绍的实现求前k大的数的方法，与堆无关。整体思想和快速排序的思路一样，把待求的数据通过一个key分割成两组，一组大于等于key的列表da，一组小于key的列表db。

此时有几种情况：

　　1. k<=0时， 数据已经找到了，直接返回[]

　　2. len(da)<=k时返回，然后在小的一组db寻找k-len(da)个剩下的数

　　3. 分割后len(da) > k，这时就继续分割这个列表

如此递归最后返回的就是前k大的数，但是这种方法返回的数并未排序。

def partition(data):
    key = data[0]
    da = []         # 保存大于等于key的值
    db = []         # 保存小于key的值
    for d in data[1:]:
        da.append(d) if d >= key else db.append(d)

    da.append(key) if len(da) < len(db) else db.append(key)  # 此处是把关键key放入长度小的列表中，使得分组均匀
    return da, db

def get_k_big_data(data, k):
    """利用快速排序的思想寻找前k大的数, 但是获得的数并未排序"""
    if k <= 0:
        return []
    elif len(data) <= k:
        return data
    else:
        da, db = partition(data)
        if len(da) > k:
            return get_k_big_data(da, k)
        else:
            return get_k_big_data(da, k) + (get_k_big_data(db, k - len(da)))

if __name__ == '__main__':
    print(get_k_big_data([5, 2, 5, 2, 4, 10, 7, 1, 3, 5, 9], 5))
    print("*" * 30)
    print(get_k_big_data([1, 3, 5, 3, 2, 6, 0, 9], 3))

控制台输出:

[5, 10, 7, 5, 9]
******************************
[6, 9, 5]

最后附上完整代码

 import math
 import pygraphviz as pgv
 from collections import Iterable

 class BinaryHeap(object):
     """一个二叉堆, 小顶堆 利用列表实现"""

     def __init__(self, max_size=math.inf):
         self._heap = [-math.inf]             # 初始值设置一个无限大的哨兵
         self.max_size = max_size

     def __len__(self):
         """求长度"""
         return len(self._heap) - 1

     def insert(self, *data):
         """向堆中插入元素"""
         if isinstance(data[0], Iterable):
             if len(data) > 1:
                 print("插入失败...第一个参数可迭代对象时参数只能有一个")
                 return
             data = data[0]
         if not len(self) + len(data) < self.max_size:
             print("堆已满, 插入失败")
             return
         for x in data:
             self._heap.append(x)
             self._siftup()
         print("插入成功")

     def _siftup(self):
         """最后插入的元素上浮"""
         pos = len(self)                     # 插入的位置
         x = self._heap[-1]                  # 获取最后一个位置元素
         while x < self._heap[pos >> 1]:     # 此处可以体现出哨兵的作用了, 当下标为0时, x一定小于inf
             self._heap[pos] = self._heap[pos >> 1]
             pos >>= 1
         self._heap[pos] = x

     def _siftdown(self, idx):
         """序号为i的元素下沉"""
         temp = self._heap[idx]
         length = len(self)
         while 1:
             child_idx = idx << 1
             if child_idx > length:
                 break
             if child_idx != length and self._heap[child_idx] > self._heap[child_idx + 1]:
                 child_idx += 1
             if temp > self._heap[child_idx]:
                 self._heap[idx] = self._heap[child_idx]
             else:
                 break
             idx = child_idx
         self._heap[idx] = temp

     def show_heap(self):
         """调试用，打印出数组数据"""
         print(self._heap[1:])

     def draw(self, filename='./heap.png'):
         """调试用，生成直观二叉树的图片文件"""
         g = pgv.AGraph(strict=False, directed=True)
         g.node_attr['shape'] = 'circle'
         idx = 1
         length = len(self)
         idx_length = pow(2, int(math.log(length, 2))) - 1
         while idx <= idx_length:
             if idx << 1 <= length:
                 g.add_edge(self._heap[idx], self._heap[idx << 1])
                 if (idx << 1) + 1 <= length:
                     g.add_edge(self._heap[idx], self._heap[(idx << 1) + 1])
             else:
                 g.add_node(self._heap[idx])
             idx += 1
         g.layout('dot')
         g.draw(filename)

     def get_min(self):
         if not len(self):
             print("堆为空")
         return self._heap[1]

     def delete_min(self):
         """删除堆顶元素"""
         if not len(self):
             print("堆为空")
             return
         _min = self._heap[1]
         last = self._heap.pop()
         if len(self):               # 为空了就不需要向下了
             self._heap[1] = last
             self._siftdown(1)
         return _min

     def create_heap(self, data):
         """直接创建一个小顶堆, 接收一个可迭代对象参数,效果同insert, 效率比insert一个个插入高,时间复杂度为n"""
         self._heap.extend(data)
         for idx in range(len(self) // 2, 0, -1):
             self._siftdown(idx)

     def clear(self):
         """清空堆"""
         self._heap = [-math.inf]  # 初始值设置一个无限大的哨兵

     def update_key(self, idx, key):
         """更新指定位置的元素, idx>=1"""
         if idx > len(self) or idx < 1:
             print("索引超出堆的数量或小于1")
             return
         self._heap[idx] = key
         self._siftdown(idx)

     def delete_key(self, idx):
         """删除指定位置的元素, idx>=1"""
         if idx > len(self) or idx < 1:
             print("索引超出堆的数量或小于1")
             return
         x = self._heap.pop()        # 取出最后一个元素代替, 保持完全二叉树, 然后调整到合适位置
         if not len(self):
             self._heap[idx] = x
             self._siftdown(idx)
   

完整代码

参考:

• 数据结构--堆的实现之深入分析
• 啊哈算法第7章第3节