hihoCoder #1151 : 骨牌覆盖问题·二 （矩阵快速幂，DP）

题意：给一个3*n的矩阵，要求用1*2的骨牌来填满，有多少种方案？

思路：

　　官网题解用的仍然是矩阵快速幂的方式。复杂度O(logn*8³)。

　　这样做需要构造一个2³*2³的矩阵，这个矩阵自乘n-1次，再来乘以初始矩阵init{0,0,0,0,0,0,0,1}后，变成矩阵ans{x,x,x,x,x,x,x,y}，y就是答案了，而x不必管。

　　主要在这个矩阵的构造，假设棋盘是放竖直的（即n*3），那么考虑在第i行进行填放，需要考虑到第i-1行的所有可能的状态（注意i-2行必须是已经填满了，否则第i行无法填到i-2行去）。放的时候有个规则，就是所放的每块1*2的骨牌，必须放有一半以上是在第i行的，而且不允许放到第i+1行去。其实就是根据3种选择来考虑变换，（1）不放（2）放横（3）放竖。

　　下图假设即将填第i+1行。

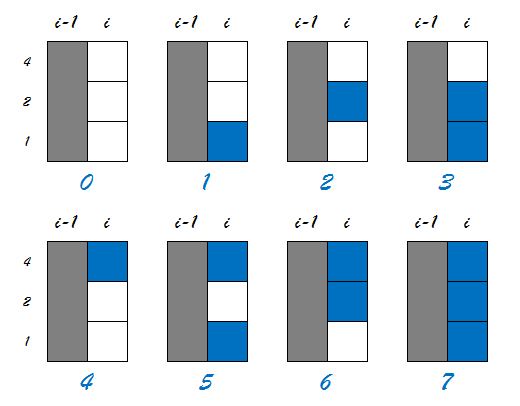
　　上图的编号代表了第i行的状态。

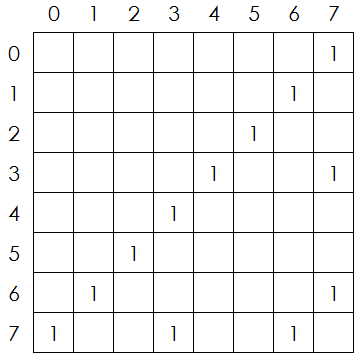
　　上图就是从第i行可以转移到第i+1行的状态。matrix[i][j]表示第i行的状态i转移到第i+1行的状态j的方案数，空格为0。

　　举个例子：第i行的状态为3，那么它只放一块骨牌时（即填满右上角的一个空格），转为4。如果放两块（即在4的基础上再放一块横的），就转为7。

　　上面只需要特别注意所假设的东西，而且要按照规则来放才行。

　　2ms

 #include <bits/stdc++.h>
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #define pii pair<int,int>
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;
 const int N=1e5+;
 const int mod=;
 int M[][]={,,,,,,,,
              ,,,,,,,,
              ,,,,,,,,
              ,,,,,,,,
              ,,,,,,,,
              ,,,,,,,,
              ,,,,,,,,
              ,,,,,,,};  //初始矩阵M

 int init[]={,,,,,,,};  //初始状态
 int tot[][], cur[][], grid[][];   //临时的矩阵

 void mul(int A[][],int B[][]) //处理两个8*8的矩阵相乘，并保存到A中
 {
     for(int i=; i<; i++)
     {
         for(int j=; j<; j++)
         {
             int tmp=;
             for(int k=; k<; k++)
             {
                 tmp+=A[i][k]*B[k][j];
                 tmp%=mod;
             }
             grid[i][j]=tmp;
         }
     }
     memcpy(A, grid, sizeof(grid));
 }

 int cal(int n)
 {
     memcpy(tot, M, sizeof(M));
     memcpy(cur, M, sizeof(M));
     n--;    //tot已经是2^0了，所以自减1.
     while(n)
     {
         if(n&==)    mul(tot, cur);   //末位为1时，累乘到tot中
         mul(cur, cur);                 //翻倍
         n>>=;
     }
     return tot[][];
 }

 int main()
 {
     freopen("input.txt", "r", stdin);
     int n;
     while(~scanf("%d",&n))    printf("%d\n", cal(n));
     return ;
 }

AC代码

　　还有一种方案仅需0ms。即递推，这个需要研究一下递推式，考虑各种情况的变化。不写了。