【贪心 计数】bzoj2006: [NOI2010]超级钢琴

这么经典的贪心我怎么现在才做啊……

Description

小Z是一个小有名气的钢琴家，最近C博士送给了小Z一架超级钢琴，小Z希望能够用这架钢琴创作出世界上最美妙的

音乐。 这架超级钢琴可以弹奏出n个音符，编号为1至n。第i个音符的美妙度为Ai，其中Ai可正可负。 一个“超级

和弦”由若干个编号连续的音符组成，包含的音符个数不少于L且不多于R。我们定义超级和弦的美妙度为其包含的

所有音符的美妙度之和。两个超级和弦被认为是相同的，当且仅当这两个超级和弦所包含的音符集合是相同的。 

小Z决定创作一首由k个超级和弦组成的乐曲，为了使得乐曲更加动听，小Z要求该乐曲由k个不同的超级和弦组成。

我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小Z想知道他能够创作出来的乐曲美妙度最

大值是多少。

Input

第一行包含四个正整数n, k, L, R。其中n为音符的个数，k为乐曲所包含的超级和弦个数，L和R分别是超级和弦所

包含音符个数的下限和上限。 接下来n行，每行包含一个整数Ai，表示按编号从小到大每个音符的美妙度。

N<=500,000

k<=500,000

-1000<=Ai<=1000,1<=L<=R<=N且保证一定存在满足条件的乐曲

Output

只有一个整数，表示乐曲美妙度的最大值。

Sample Input

4 3 2 3
3
2
-6
8

Sample Output

11

---

题目分析

定位：是一道堆例题

首先注意到k的规模不大，那么可以枚举k次。

考虑固定右端点，那么可以预处理出它合法的左端点以及前缀和最小的位置。

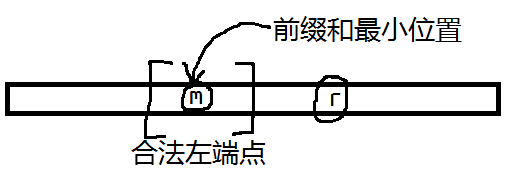
因为不能重复，所以用过的$l$对$r$不能再用。那么如果$r$再一次被当做右端点，$l'$要么在$l$左边要么在$l$右边。因此再把剩下的两个状态处理出来就可以了。

状态用一个五元组保存就行了；查询静态最优值则可以用st表预处理。

 #include<bits/stdc++.h>
 typedef long long ll;
 const int maxn = ;
 const int maxLog = ;

 struct node
 {
     int L,R,i,v,p;
     node(int a=, int b=, int c=, int d=, int e=):L(a),R(b),i(c),v(d),p(e) {}
     bool operator < (node a) const
     {
         return v < a.v;
     }
 };
 int n,k,L,R,s[maxn],lgs[maxn],f[maxn][maxLog];
 std::priority_queue<node> q;
 ll ans;

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 void STinit()
 {
     for (int i=; i<=n; i++) f[i][] = i;　　//这里要处理i=0，因为查询时候的[l',r']是[l,r]的前缀位置，即[l-1,r-1]
     for (int j=; (<<j)<=n; j++)
         for (int i=; i<=n; i++)
             if (i+(<<j) < n){
                 int l = f[i][j-], r = f[i+(<<(j-))][j-];
                 if (s[l] > s[r]) f[i][j] = r;
                 else f[i][j] = l;
             }
 }
 int STquery(int l, int r)
 {
     l--, r--;
     int c = lgs[r-l+], x = f[l][c], y = f[r-(<<c)+][c];
     return s[x] > s[y]?y:x;
 }
 int main()
 {
     n = read(), k = read(), L = read(), R = read(), lgs[] = -;
     for (int i=; i<=n; i++) s[i] = s[i-]+read();
     for (int i=; i<=n; i++) lgs[i] = lgs[i>>]+;
     STinit();
     for (int i=; i<=n; i++)
     {
         int lbd = std::max(i-R+, ), rbd = std::max(i-L+, );
         if (i-rbd+ < L) continue;
         int pos = STquery(lbd, rbd);
         q.push(node(lbd, rbd, i, s[i]-s[pos], pos+));
     }
     while (k--)
     {
         node tt = q.top();
         q.pop(), ans += tt.v;
         int lbd = tt.L, rbd = tt.R, i = tt.i, p = tt.p, pos;
         if (lbd < p){
             pos = STquery(lbd, p-);
             q.push(node(lbd, p-, i, s[i]-s[pos], pos+));
         }
         if (rbd > p){
             pos = STquery(p+, rbd);
             q.push(node(p+, rbd, i, s[i]-s[pos], pos+));
         }
     }
     printf("%lld\n",ans);
     return ;
 }

END